== 問題以上，答以下 ==
• 文章題では，問題をじっくり読むことが大切です．
• ここでは答を気にせずに，問題を読むことに集中しましょう．
《もとの問題》
右の図のように，ＡＢ＝4cm，BC=2cmの長方形ＡＢＣＤがある．平面上でこの長方形を頂点Ｃを中心に90 だけ時計回りに回転させたとき，次の問い(1)(2)に答えよ．
(1)
辺ＡＢが描く図形として，正しいものはどれか．下の略図(ア)〜(オ)から選べ． |
 |
(2)
(1)で辺ＡＢの描いた図形の面積を求めよ．
（「京都府 平成11年度」問題の引用）
|
《答える前に》
(1)(2)では「何が」描いた図形について，質問しているのですか．
(正しいものを選びなさい↓)
長方形ＡＢＣＤ， 辺ＡＢ， 点Ａと点Ｂ
|
 |
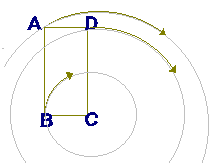
点Ｃを中心として，ＣＡ，ＣＢ，ＣＤを半径とする円を描くと，点Ａ，Ｂ，Ｄの動いたあとは右図のようになります．上の問題(1)で「点Ａと点Ｂ」の動いたあとが「両方とも」正しく描かれている図はどれですか．
(正しいものを選びなさい↓)
(ア) (イ) (ウ) (エ) (オ)
|
 |
|
|
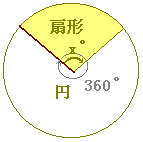
さて，ちょうど半径になっているものを，右図のようにｘだけ回転したとき，この半径が動いたあとは，扇形になります．
半径がｒの扇形の図形の面積は，中心角に比例します．中心角ｘの扇形の面積をＳ，中心角360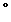の円の面積πｒ2を用いると，Ｓ：πｒ2＝ｘ：360 です．これを変形して，Ｓをπ，ｒ，ｘで表わすと，(正しいものを選びなさい↓)
 ,  ,  ,  ,  , 
|
 |
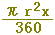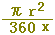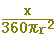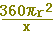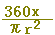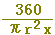
ｘが90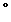のときは，
(正しいものを選びなさい↓)
 ,  ,  ,  ,  ,
|
|
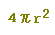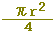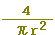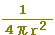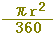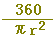
| 上の問題(2)のように，半径以外のものを回転させたとき，動いたあとにできる図形は
のように，凹凸を埋めると「扇形」や「中抜きの扇形」になります． |
|
| 上の例Ａにおいて，円の半径が２√5で回転角が９０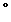のとき，Ｌ字形の動いたあとにできる図形の面積は(正しいものを選びなさい↓)
４π， ５π， ４√5π， 20π
上の例Ｂにおいて，外の円の半径が２√5，中の円の半径が２で回転角が９０のとき，線分の動いたあとにできる図形の面積は(正しいものを選びなさい↓)
π， ４π， ５π， ３√5π， 16π
|
|
《類題》
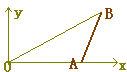
右の図のように，△ＯＡＢがあり，Ｏ(0,0)，Ａ(6,0)，Ｂ(8,4)とする．このとき，次の問い(1)(2)に答えよ．
(1)
平面上で三角形ＯＡＢを点Ｏを中心に90時計回りに回転させたとき，辺ＡＢが描く図形として正しいものはどれか．下の略図(ア)〜(エ)から選べ． |
 |
(2)
(1)で辺ＡＢの描いた図形の面積を求めよ．ただし，円周率はπとする．
（「京都府 平成7年度」問題の引用）
|
《類題》
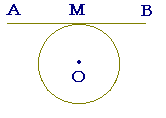
右の図のように，長さ4cmの線分ＡＢがあり，その中点Ｍで円Ｏに接している．
このとき，次の問い(1)(2)に答えよ．
(1)
線分ＡＢが，中点Ｍで円に接しながら，円Oのまわりを１周したとき，線分ＡＢの描く図形として正しいものはどれか，下の略図(ア)〜(エ)から選べ． |
 |
(2)
(1)で線分ＡＢの描いた図形の面積を求めよ．ただし，円周率はπとする．
（「京都府 平成9年度」問題の引用）
|
《答える前に》
(正しいものを選びなさい↓)
(1)
(ア) (イ) (ウ) (エ)
|
|
(2)
円Ｏの半径はいくらですか．(正しいものを選びなさい↓)
１， ２， √3， ４， 書いてない
|
|
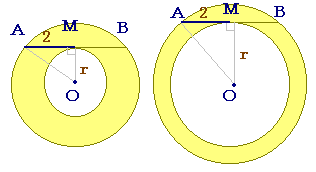
下の２つの図で黄色で示したドーナツ状の図形の面積が，円Ｏの半径ｒに無関係に一定になるという性質があれば，(2)の問題が解けるはずです．
下の図（どちらでも）において，外側に描かれた円の半径をｒを用いて表わすと，どうなりますか．(正しいものを選びなさい↓)
 ，  ，  ，  ，  ，  ， 
|
|
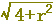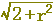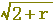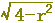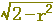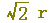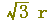
上の図で黄色で示したドーナツ状の図形(１つ)の面積は，いくらですか．
(正しいものを選びなさい↓)
２π， ３π， ４π
|
|
|
