|
【はじめに】 x の方程式では，左辺と右辺が等しくなるような x の値を求めます． 例 1個 80 円のパンと１個 100 円の牛乳を合計 8個買うと合計 700 円になった．パンを何個買ったか求めたいとき，パンを x 個買ったとすると，
この方程式を解けば，パンの個数 x が求まります．（x=5） 【解説】 ○ 「方程式を解く」ことは後の頁に回して，この頁では「文章題から方程式を作る」ために必要な式を考えます．
○ このように，文章題から方程式を作るには，１つずつの式を正確に組立てなければなりません． ○ 以下の練習問題は，文章題の方程式を解くとき必要となる「１つずつの式」を正確に作る練習です．
「１つずつの部品がきっちりできていないと，車は動かない」のと同様に，「１つずつの式がきっちりできていないと，方程式はできません」．
|
|||||||||||||||||||||
|
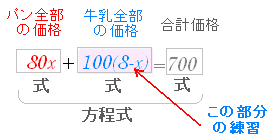
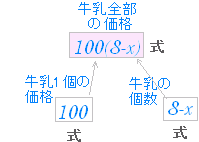
○次の各文章で指示された量を文字 x を用いて表わしなさい． 半角英数字で答えるものとし，文字 x は小文字とします
問１
コッペパンとあんぱんを合計 15 個買うものとする．あんぱんを x 個買うものとするとコッペパンは何個買うことになるか．x で表わしなさい．
15−xになります
|
問2
和菓子が洋菓子よりも 3 個多くある. 和菓子の数を x (個)とするとき，洋菓子の個数を x で表わしなさい．
和菓子が洋菓子よりも3個多いのだから，洋菓子は和菓子xよりも3個少なくなります．→ x−3
|
問3
Ａ地点からＢ地点まで移動するのに，分速 100 (m)で歩くと予定よりも 10 分早く到着する．予定の時間の長さを x (分)とすると，Ａ地点からＢ地点まで分速 100 (m)で何分歩くことになるか．x で表わしなさい．
予定xよりも 10 分早く到着するのだから x−10
|
問4
Ａ地点からＢ地点まで移動するのに，分速 100 (m)で歩くと予定よりも 10 分早く到着する．予定の時間の長さを x (分)とすると，Ａ地点からＢ地点まで何mになるか．x で表わしなさい．
予定xよりも 10 分早く到着するのだから x−10（分）歩くことになる
分速 100 (m)だから，距離は100(x−10) |
問5
分速 100 (m)で歩く人がスタートしてから 6 分後に自転車で追いかける．自転車で走った時間を x (分)とすると，歩く人は何分歩いたことになるか．x で表わしなさい．
歩く時間は，自転車で走る時間 x (分)よりも 6 (分)多いからx+6 (分)
|
問6
分速 100 (m)で歩く人がスタートしてから 6 分後に自転車で追いかける．自転車で走った時間を x (分)とすると，歩く人は自転車に追いつかれるまでに何m歩いたことになるか．x で表わしなさい．
歩く時間は，自転車で走る時間 x (分)よりも 6 (分)多いからx+6 (分)歩いている．
分速 100 (m)で歩いているから，距離は分速 100(x+6) (m) |
問7
お菓子を子どもたちに分けるとき，一人 5 個ずつ分けるにはお菓子は 3 個足りない．子どもの人数を x (人)とすると，お菓子の個数を x で表わしなさい．
x (人)の子どもに一人 5 個ずつ分けるには，本当は 5x 個のお菓子が必要
これよりも3個少ないのだから 5x−3 |
問8
体育館の長いすに生徒が座るとき，１脚当り 3 人ずつ座ると 16 人分の席が足りない．長いすの数を x (脚)とするとき，いすに座れる生徒数を x で表わしなさい．
長いす x (脚)に１脚当り 3 人ずつ座るのだから，座れる人数は 3x 人
|
問9
体育館の長いすに生徒が座るとき，１脚当り 3 人ずつ座ると 16 人分の席が足りない．長いすの数を x (脚)とするとき，生徒数を x で表わしなさい．
座れる人数 3x よりも生徒数は16人多いから，生徒数は 3x+16
|
 ...（携帯版）メニューに戻る...（PC版）メニューに戻る |
