１次方程式の解き方

== １次方程式の解き方 ==

## 違うページを見ていませんか? ##
　このページは中学1年生向けの「１次方程式の解き方」を解説したものです．次のような質問がかなり多いので注意してください．
•「－X－5Xの解き方がのっていなくてわからなかった」
•「教えて欲しいところが載ってなかった」
•「10-3X-8-4X」
•「ー9yーyなどのやりかたなどのせてほしい」
⇒ これらは，もっと前の「文字式の変形」の項目にあります．

○　１次方程式を解くとは
3x+5=−1 …(1) のように未知数xを含む等式をxについての方程式といいます。
この頁では、１次方程式から「等式の性質」を使って解を求める方法を学びます。
x=···の形をした式を解といいます。解を求めるためには、左辺が１つのxだけになるように変形します。

○　等式の性質

(I)等式の両辺に同じ数を「引いたり」「足したり」しても、等式は成り立つ。（左辺と右辺には必ず同じ変形をしなければなりません。）

A=B⇒A+C=B+C
A=B⇒A−C=B−C

【例】
○ x−3=1⇒x−3+3=1+3

※左辺の−3を取り除くには、「両辺に」+3を付けます。
※左辺と右辺には必ず同じ変形をしなければなりません。
※左辺の−3+3は+0になって消えます。右辺の1+3は4になります。

⇒x=4 …（解）
○ x+3=1⇒x+3−3=1−3

※左辺の+3を取り除くには、「両辺に」−3を付けます。
※左辺と右辺には必ず同じ変形をしなければなりません。
※左辺の+3−3は+0になって消えます。右辺の1−3は−2になります。

⇒x=−2 …（解）

(II)等式の両辺に同じ数を「割ったり」「掛けたり」しても、等式は成り立つ。（ただし、0で割ってはいけない。）（左辺と右辺には必ず同じ変形をしなければなりません。）

A=B⇒A×C=B×C

A=B⇒A×=B×

【例】
○ 3x=6⇒3x×=6×

※左辺の3は「掛け算」として付いているので、これを取り除くには、「両辺に」×を付けます。

※左辺と右辺には必ず同じ変形をしなければなりません。
※左辺の3×は×1になって消えます。右辺の6×は2になります。

⇒x=2 …（解）
○ =2⇒×3=2×3

※左辺の3は「割り算」として付いているので、これを取り除くには、「両辺に」×3を付けます。

※左辺と右辺には必ず同じ変形をしなければなりません。
※左辺の×3は×1になって消えます。

右辺の2×3は6になります。

⇒x=6 …（解）

　中学１年生で、方程式がうまく解けない人は、上の(I)と(II)を使う場面を混同していることがあります。
　特に、3x=6のような方程式で、両辺から3を引いても左辺の3は取り除けません。
　3xのように3とxとが「掛け算」で結びついているときは、「割り算（分数の掛け算）」で3を取り除きます。

問題１　次の空欄に入る式を右の赤枠の中から選んで入れなさい。

（はじめに左の空欄を選び、続いて右の式を選びなさい。正しければ代入されます、間違っていれば元に戻ります。）

(1)x−2=5

x−2+?=5+?

x=?

(2)x+4=7

x+4−?=7−?

x=?

(3)2x=12

2x×?=12×?

x=?

(4)=−3

×?=−3×?

x=?

≪式≫

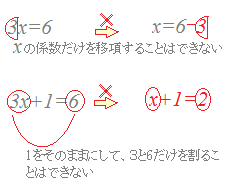
問題２　次の空欄に入る式を右の赤枠の中から選んで入れなさい。

（はじめに空欄を選び、続いて右の式を選びなさい。正しければ代入されます、間違っていれば元に戻ります。）

(1)x−3=−7

x−3+?=−7+?

x=?

(2)x+5=−3

x+5−?=−3−?

x=?

(3)−3x=2

−3x×(?)=2×(?)

x=?

(4)−=

−×(?)=×(?)

x=?

≪式≫

○　xが両辺にあるとき

　xが両辺にある１次方程式では、xを含む項を左辺に集め、定数項を右辺に集めるように変形します。

【例】

○ 5x−2=3x+4
5x−3x−2=3x−3x+4 （これは「引き算」）	右辺の3xを取り除くには、「両辺に」−3xを付けます。（(I)の性質はxを含んだ式にも使えます。）
2x−2=4	xの係数を簡単にします。
2x−2+2=4+2 （これは「足し算」）	左辺の−2を取り除くには、「両辺に」+2を付けます。（(I)の性質）
2x=6	定数項を簡単にします。
2x×=6× （ここだけが「割り算」：分数の「掛け算」）	左辺の2を取り除くには、「両辺に」×を付けます。（(II)の性質）
x=3	…（答）

【変形する順序が重要】
　5x−2=3x+4のような方程式を変形するときは、

(I)の足し算・引き算だけを使って

ax=bの形にする。

最後に、
(II)を使って掛け算・割り算をする。

問題３　次の空欄に入る式を下の赤枠の中から選んで入れなさい。

（はじめに空欄を選び、続いて下の式を選びなさい。正しければ代入されます、間違っていれば元に戻ります。
背景の灰色がなくて単に?と書かれている箇所は，上の式が埋まれば自動的に入ります．）

(1)5x+3=3x+7

5x−?x+3=3x−?x+7
?x+3=7
?x+3−?=7−?
?x=?
?x×?=4×?
x=?

(2)−3x+8=−5x−6

−3x+?x+8=−5x+?x−6
?x+8=−6
?x+8−?=−6−?
?x=?
?x×?=?×?
x=?

≪式≫

○　移項という考え方
　次の変形のように「両辺から4を引く」計算の最初と最後を見ると、4の符号を変えて他方の辺に移動したことになっています。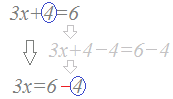

　また、次の変形のように「両辺から2xを引く」計算の最初と最後を見ると、2xの符号を変えて他方の辺に移動したことになっています。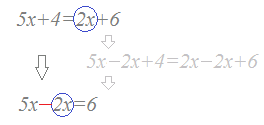

　このように、上の(I)で述べた変形は、「項になっているものは、符号を変えて他方の辺に移動してよい」とまとめることができます。
　これを「移項」といいます。

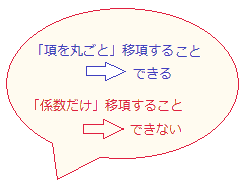
ax+b=cx+d cxを移項する ax−cx+b=d	ax+b=cx+d bを移項する ax=cx+d−b
ax+b=−cx+d −cxを移項する ax+cx+b=d	ax−b=cx+d −bを移項する ax=cx+d+b

【移項はとても危険、しかし便利】

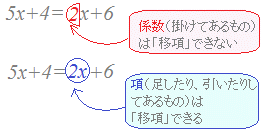　図のように、移項できるのは足し算や引き算で区切られた「項」丸ごとです。係数だけを移項できると考えてはいけません。

　１次方程式の計算がうまくできない中学生が最も間違いやすいのが移項です。

ax+b=cx+d

こんな計算は間違い
ax+b−c=d

ax+b=−cx+d

こんな計算は間違い
ax+b+c=d

問題４　次の空欄に入る式を下の赤枠の中から選んで入れなさい。

（はじめに空欄を選び、続いて下の式を選びなさい。正しければ代入されます、間違っていれば元に戻ります。）

(1)3x=7x+8 の7xを移項すると
?=8

(2)7x=−3x+8 の−3xを移項すると
?=8

(3)7x+8=3x の8を移項すると
7x=?

(4)−7x−8=−3x の−8を移項すると
−7x=?

≪式≫

※（自由研究）
　あなたが解きたいと思う問題を書き込んで［解く］というボタンを押してください．

ただし
• 整数係数の問題に限ります．
• 両辺のxの係数が同じ問題は解けません

解く消す

○　元の問題が引き算になっているときは，次の例のように係数をマイナスの符号に変えて使ってください．

3x−4=5x+7

(3)x+(−4)=(5)x+(7)

○　元の問題でxの項と定数項の順序が逆になっているときは，次の例のようにxの項を前にして使ってください．

6−7x=5x+7

(−7)x+(6)=(5)x+(7)

○　書いてないときの注意
元の問題で「xの係数が書いてない」ものは(1)xを表します．

3x+4=x+7

(3)x+(4)=(1)x+(7)

3x+4=−x+7

(3)x+(4)=(−1)x+(7)

　元の問題で「数字だけの項，すなわち定数項」がないときは，その部分は0にします.

3x=x+7

(3)x+(0)=(1)x+(7)

3x+4=−x

(3)x+(4)=(−1)x+(0)

	xの係数^(*1)	定数項^(*2)
書いてないもの	0ではない 1を表す	1ではない 0を表す

^(*1)･･･掛け算で何も掛けないのは　×1
^(*2)･･･足し算で何も足さないのは　＋0

○　元の問題が小数係数のときは，次の例のように両辺を10倍，100倍，...して整数係数に変えて使ってください．

0.3x+0.4=0.8x+0.6

(3)x+(4)=(8)x+(6)

○　元の問題が分数係数のときは，次の例のように両辺に分母の最小公倍数を掛けて整数係数に変えて使ってください．（最小公倍数が分かりにくいときは，全部の分母を掛けてもよい）

x+=x−

(2)x+(3)=(6)x+(−5)

...（携帯版）メニューに戻る

...（PC版）メニューに戻る

■［個別の頁からの質問に対する回答］[１次方程式の解き方について／17.4.1］

公式がわからない。
＝＞［作者］：連絡ありがとう．公式は書いてあり，その使い方の例も書いてあります．これで公式がわからないということですので，新中学１年生で，まだ習っていないという場合でしたらあり得ますが，それ以上の年齢の方ですと結構大変な話をしていることになります．
すなわち，１次方程式の解き方の変形公式は，「水や空気のように」「呼吸をするように」至る所で使うので，これが公式であると一々考えているようでは生活できません．息の仕方の「公式が分からない」ので息をしていないと言っているのと同じくらいの話になります．普通の中学生は，最終的には何百回，何千回も練習して，特に考えなくても変形できるところまでやるからできるようになる訳で，初めからできる人はいません．

■［個別の頁からの質問に対する回答］[１次方程式の解き方について／17.2.26］

わかりやすい
＝＞［作者］：連絡ありがとう．