数列の和の極限

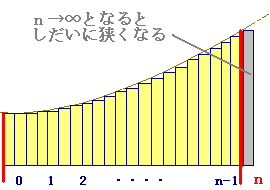
　次の図において，ｙ＝ｘ^２，x軸，ｘ＝１の直線で囲まれた図形の面積を求めることを考えます．この図形は，長方形でもなく，三角形でもなく，円でもないので，小中学校で習った面積の求め方では求められません．むしろ，そのような面積が定義できるのか？と疑うことが，ここで扱うテーマを理解する早道です．
■
　そもそも，１×１の正方形の面積が１です（下図）．これより小さい図形は，0.1の長方形が何個入るかに応じて，次の桁を決めます．以下同様にして，0.01，0.001，．．．の正方形・長方形を入るだけ埋めて，求める図形がちょうど埋まるまで繰り返します．
　素朴に考えれば，境界線がｙ＝ｘ^２のような曲線では，正方形や長方形をどう並べても埋まりそうもありません．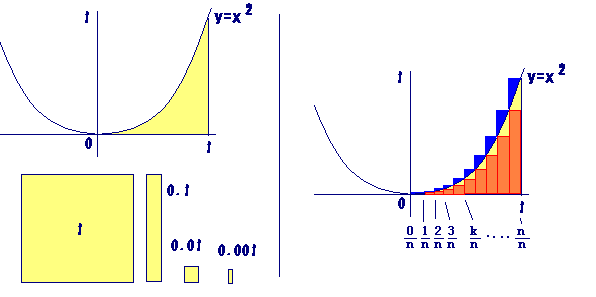

■　右図のように，少し大き目の長方形の和（上組）と少し小さ目の長方形の和（下組）を考えます．もし，求める図形に面積Ｓがあるとすれば，

＜Ｓ＜となるはずです．
■　長方形の横幅を小さくしていったとき（→０），もしとの面積が一致したら，その一致した値を面積Ｓの定義とすることは合理的です．

≪はさみうち論法≫
an<S<bnで $\lim_{n\rightarrow \infty}a_n=\lim_{n\rightarrow \infty}b_n=A$ ならば $S=A$

を用いると，下組と上組の極限が等しくなっとき，その等しい値を「面積」と定義します．

■　下組

$=(\frac{0}{n})^2\frac{1}{n}+ (\frac{1}{n})^2\frac{1}{n}+ \cdots + (\frac{k-1}{n})^2\frac{1}{n} + \cdots + (\frac{n-1}{n})^2\frac{1}{n}$
＝

＝

＝　→　（ｎ→∞のとき）
■　上組

$=(\frac{1}{n})^2\frac{1}{n}+ (\frac{2}{n})^2\frac{1}{n}+ \cdots + (\frac{k}{n})^2\frac{1}{n} + \cdots + (\frac{n}{n})^2\frac{1}{n}$
＝

＝

＝　→　（ｎ→∞のとき）
■　以上により，S=・・・これが，求める図形の面積です．

定積分と面積の関係

　上の図形の面積は，定積分で表わされます．
　これらを比較すると，
$(\frac{1}{n})^2\frac{1}{n}+ (\frac{2}{n})^2\frac{1}{n}+ \cdots + (\frac{k}{n})^2\frac{1}{n} + \cdots (\frac{n-1}{n})^2\frac{1}{n} + (\frac{n}{n})^2\frac{1}{n}$
$=\int_0^1x^2 dx$
すなわち，

上組と下組は等しいので，　も成立します．

数列の和の極限を定積分に直す方法

■　数列の和の極限を定積分に直すには，次のような図を考えます．

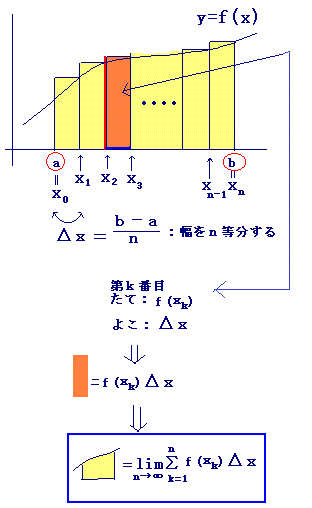
≪公式≫･･･次のように対応させて覚える

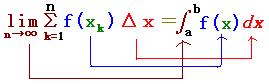
■この公式を使うには，「各部品」を正確に対応させることが大切です．（初めは，大変難しいものです．）

＜要点＞
１　まず，Δｘ（通常は１／ｎ）を分離すること
→これがｄｘになります．
(Σ記号の初項から末項までの項数ｎ個の等分となっている)
２　ｘ_ｋを決める　→　ｆ（ｘ_ｋ）を決める　→　ｆ（ｘ）を決める．
３　limΣ→∫　とします．
４　ｘ_０＝ａ，ｘ_ｎ＝ｂ　とします．
　　ｂ－ａ＝１でない場合は１の段階でΔｘを調整します．

(例１)　次の極限値を定積分に直し，その値を求めなさい．

(考え方)

【ポイント：Δｘの役割】

１／ｎ＝Δｘがなければ積分できません．なければ作ります．このために，１／ｎでくくります．（区間の幅は１）

ｋ／ｎ＝ｘ_ｋ　→　ｆ（ｘ_ｋ）＝　→　ｆ（ｘ）＝　とします．

ｋ／ｎ＝ｘ_ｋ　→　ａ＝ｘ_０＝０，　ｂ＝ｘ_ｎ＝１（区間の幅は１でよい．）

limΣを∫にします．

（答案）

＝＝

(例２)　次の極限値を定積分に直し，その値を求めなさい．

(考え方１)

【ポイント：区間の幅】

１／ｎでくくります．（区間の幅は１）
ｘ_ｋ＝ｋ／ｎ　→　ｆ（ｘ_ｋ）＝πsinπｘ_ｋ

　→　f(ｘ)＝πsinπｘ

ｘ_ｋ＝ｋ／ｎ　→ａ＝ｘ_０＝０，ｂ＝ｘ_ｎ＝１

（区間の幅は１）

limΣを∫にします．

（答案１）

＝

(考え方２)

π／ｎ＝Δｘとします．（区間の幅はπ）
ｘ_ｋ＝ｋπ／ｎ　→　ｆ（ｘ_ｋ）＝sinｘ_ｋ

　→　f(ｘ)＝sinｘ

ｘ_ｋ＝ｋπ／ｎ　→ａ＝ｘ_０＝０，ｂ＝ｘ_ｎ＝π

（区間の幅はπ）

limΣを∫にします．

（答案２）

＝

(例３)　次の極限値を定積分に直し，その値を求めなさい．

【ポイント：ｘ_ｋ←→ｆ（ｘ_ｋ）←→ｆ（ｘ）】

(考え方１)

１／ｎでくくります．（区間の幅は１）
＝
ｘ_ｋ＝ｋ／ｎとおくと，　ｆ（ｘ_ｋ）＝（１＋ｘ_ｋ）^２

ｆ（ｘ）＝（１＋ｘ）^２

ａ＝ｘ_０＝０，　ｂ＝ｘ_ｎ＝１（区間の幅は１）
limΣを∫にします．

（答案１）

＝

(考え方２)

１／ｎでくくります．（区間の幅は１）
＝
ｘ_ｋ＝１＋ｋ／ｎとおくと，　ｆ（ｘ_ｋ）＝ｘ_ｋ^２

ｆ（ｘ）＝ｘ^２

ａ＝ｘ_０＝１，　ｂ＝ｘ_ｎ＝２（区間の幅は１）
limΣを∫にします．

（答案２）

＝

(例４)　次の極限値を定積分に直し，その値を求めなさい．

(考え方)

【ポイント：皮1枚過剰→引いてから足す】

　または　　が　　に等しいので，

　では，「皮１枚分」多いことになります．（次の図参照）

→

この場合，「大した違いはないから」などとあいまいにせず，「過剰分を引いて定積分を完成してから」「右端（または左端）の項を加え」ます．

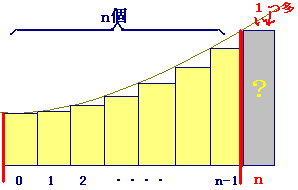（答案）

＝

(例５)　次の極限値を定積分に直し，その値を求めなさい．

(考え方)

【ポイント：皮1枚不足→足してから引く】

　または　　が　　に等しいので，この問題では「皮１枚分不足」です．
この場合，「不足分を埋めて，定積分を完成してから」「引きます」．（次の図参照）（埋めるのは，左端でもよい．）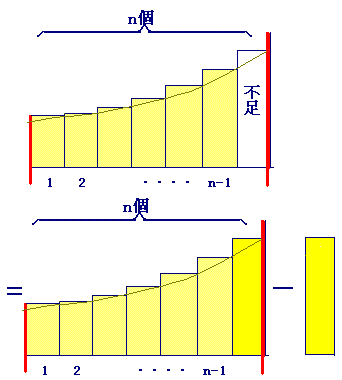

（答案）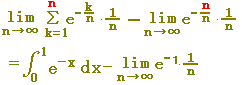

＝

(例６)　次の極限値を定積分に直し，その値を求めなさい．

【ポイント：３ｎ等分→Δｘ＝１／(３ｎ)】

(考え方)
k=1～3nなので，短冊の横幅としてΔｘ＝１／（3n）を使うと，図形を想像しやすくなります．
（答案）

※　（例１）でｎに３ｎを代入したものと一致します．

(例７)　次の極限値を定積分に直し，その値を求めなさい．

【ポイント：ａ→初項，ｂ→末項】

(考え方)
ｋ＝ｎ＋１～３ｎ　なので，項数は２ｎです．
Δｘ＝１／（2n），ｘ_ｋ＝ｋ／（2n）とおくとき，
ａ＝ｘ_ｎ＝１／２，ｂ＝ｘ_３ｎ＝３／２　です．
（答案）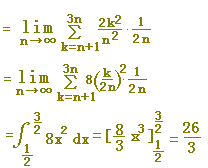

○この項目をはじめて学ぶ場合，次の問題は難しく感じるはずです．
○慣れるまでは，解説を順に読んで，もう一度やったときに自分で解けるようになればよいでしょう．
○解説を読めば，毎回同じことをしていることが分かり，流れが読めるようになります．

$\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{1}{n}\sqrt{1+ \frac{k}{n}}$
において
$\frac{1}{n}=\Delta x\rightarrow dx,\hspace{10}\frac{k}{n}=x_k\rightarrow x$
とおくと
$f(x_k)=\sqrt{1+ x_k}\rightarrow f(x)=\sqrt{1+ x}$
$a=x_0=0, \hspace{10} b=x_n=1$
となるから
（原式）= $\int_0^1 \sqrt{1+ x}dx$
→解説を隠す← $\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{k}{n^2+ k^2}$
においては，Δx となるべき 1/n がないから，これを作る
分母をn²でくくると
$\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{k}{1+ (\frac{k}{n})^2}\times \frac{1}{n^2}$
1/n² のままではｎ等分にならないので1/n×1/nに分ける
$\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{\frac{k}{n}}{1+ (\frac{k}{n})^2}\times \frac{1}{n}$
$\frac{1}{n}=\Delta x\rightarrow dx,\hspace{10}\frac{k}{n}=x_k\rightarrow x$
とおくと
$f(x_k)=\frac{x_k}{1+ x_k^2}\rightarrow f(x)=\frac{x}{1+ x^2}$
$a=x_0=0, \hspace{10} b=x_n=1$
となるから
（原式）= $\int_0^1 \frac{x}{1+ x^2}dx$ →解説を隠す← $\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{1}{n^2}(\sqrt{k}+ \sqrt{n})^2$
において，Δx となるべき 1/n を後ろに回して見やすくする
$\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{(\sqrt{k}+ \sqrt{n})^2}{n}\times \frac{1}{n}$
真ん中の式の分数の形を整える
$\lim_{n\rightarrow \infty}\sum_{k=1}^n (\frac{\sqrt{k}+ \sqrt{n}}{\sqrt{n}})^2\times \frac{1}{n}$
$=\lim_{n\rightarrow \infty}\sum_{k=1}^n (\sqrt{\frac{k}{n}}+ 1)^2\times \frac{1}{n}$
$\frac{1}{n}=\Delta x\rightarrow dx,\hspace{10}\frac{k}{n}=x_k\rightarrow x$
とおくと
$f(x_k)=(\sqrt{x_k}+ 1)^2\rightarrow f(x)=(\sqrt{x}+ 1)^2$
$a=x_0=0, \hspace{10} b=x_n=1$
となるから
（原式）= $\int_0^1 (\sqrt{x}+ 1)^2 dx$ →解説を隠す← $\lim_{n\rightarrow \infty}\frac{1}{n\sqrt{n}}\sum_{k=1}^n \sqrt{k}$
Σ記号の中では，ｋが変数でｎは定数だから
$\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{\sqrt{k}}{n\sqrt{n}}$
Δx となるべき 1/n を後ろに回して見やすくする
$\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{\sqrt{k}}{\sqrt{n}}\times \frac{1}{n}$
$=\lim_{n\rightarrow \infty}\sum_{k=1}^n \sqrt{\frac{k}{n}}\times \frac{1}{n}$
$\frac{1}{n}=\Delta x\rightarrow dx,\hspace{10}\frac{k}{n}=x_k\rightarrow x$
とおくと
$f(x_k)=\sqrt{x_k}\rightarrow f(x)=\sqrt{x}$
$a=x_0=0, \hspace{10} b=x_n=1$
となるから
（原式）= $\int_0^1 \sqrt{x} dx$ →解説を隠す← $\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{(n+ k)^2}{n^3}$
Δx となるべき 1/n を後ろに回して見やすくする
$\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{(n+ k)^2}{n^2}\times \frac{1}{n}$
$=\lim_{n\rightarrow \infty}\sum_{k=1}^n \Bigl(\frac{n+ k}{n} \Bigr)^2\times \frac{1}{n}$
$=\lim_{n\rightarrow \infty}\sum_{k=1}^n \Bigl(1+ \frac{k}{n} \Bigr)^2\times \frac{1}{n}$
$\frac{1}{n}=\Delta x\rightarrow dx,\hspace{10}\frac{k}{n}=x_k\rightarrow x$
とおくと
$f(x_k)=(1+ x_k)^2\rightarrow f(x)=(1+ x)^2$
$a=x_0=0, \hspace{10} b=x_n=1$
となるから
（原式）= $\int_0^1 (1+ x)^2 dx$ →解説を隠す← $\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{1}{n^2}\sqrt{n^2+ k^2}$
Δx となるべき 1/n を後ろに回して見やすくする
$\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{1}{n}\sqrt{n^2+ k^2}\times \frac{1}{n}$
$=\lim_{n\rightarrow \infty}\sum_{k=1}^n \sqrt{1+ \frac{k^2}{n^2}}\times \frac{1}{n}$
$=\lim_{n\rightarrow \infty}\sum_{k=1}^n \sqrt{1+ (\frac{k}{n})^2}\times \frac{1}{n}$
$\frac{1}{n}=\Delta x\rightarrow dx,\hspace{10}\frac{k}{n}=x_k\rightarrow x$
とおくと
$f(x_k)=\sqrt{1+ x_k^2}\rightarrow f(x)=\sqrt{1+ x^2}$
$a=x_0=0, \hspace{10} b=x_n=1$
となるから
（原式）= $\int_0^1 \sqrt{1+ x^2} dx$ →解説を隠す← $\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{1}{\sqrt{n^2+ k^2}}$
1/n を作るために分母をnでくくる（根号内は n²で割る）
$\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{1}{\sqrt{1+ \frac{k}{n}}\times n}$
$=\lim_{n\rightarrow \infty}\sum_{k=1}^n \frac{1}{\sqrt{1+ \frac{k}{n}}}\times \frac{1}{n}$
$\frac{1}{n}=\Delta x\rightarrow dx,\hspace{10}\frac{k}{n}=x_k\rightarrow x$
とおくと
$f(x_k)=\frac{1}{\sqrt{1+ x_k}}\rightarrow f(x)=\frac{1}{\sqrt{1+ x}}$
$a=x_0=0, \hspace{10} b=x_n=1$
となるから
（原式）= $\int_0^1 \frac{1}{\sqrt{1+ x}} dx$ →解説を隠す←

...（携帯版）メニューに戻る

...（PC版）メニューに戻る