|
*** ���w�V�i�O�p,����,�w��,�ΐ������܂ށj ***
 ��ϕ��̊�{ ��ϕ��̊�{
 ��ϕ��̒u���ϕ� ��ϕ��̒u���ϕ�
 ��(2) ��(2) ��ϕ��̕����ϕ� ��ϕ��̕����ϕ�
 �������̒�ϕ� �������̒�ϕ� �O�p���i��Βl�t���j�̒�ϕ� �O�p���i��Βl�t���j�̒�ϕ� lim���ƒ�ϕ��̊W lim���ƒ�ϕ��̊W
 �Ȑ��ň͂܂ꂽ�}�`�̖ʐ� �Ȑ��ň͂܂ꂽ�}�`�̖ʐ�
 ��(2)�}��ϐ� ��(2)�}��ϐ�
 ��(3) ��(3)
 ��ϕ��̑Q���� ��ϕ��̑Q����
 �Ȑ��̒��� �Ȑ��̒���
*** �������� ***
 ��]�̂̑̐� ��]�̂̑̐�
 �L�`�ϕ� �L�`�ϕ�
 �d�ϕ� �d�ϕ�
 �ȒP�ȏd�ϕ��̌v�Z �ȒP�ȏd�ϕ��̌v�Z �ϕ��̈悪�ϐ��Ɉˑ�����ꍇ�̏d�ϕ� �ϕ��̈悪�ϐ��Ɉˑ�����ꍇ�̏d�ϕ� �ϕ������̕ύX �ϕ������̕ύX
 �ϐ��ϊ��F���R�r�s�� �ϐ��ϊ��F���R�r�s��
|

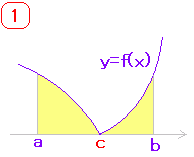
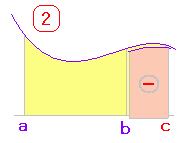
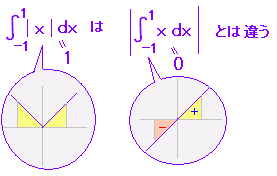
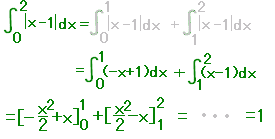
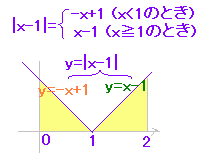
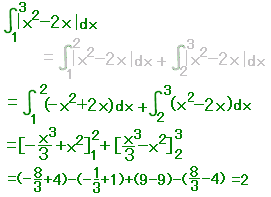
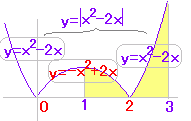

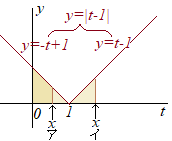
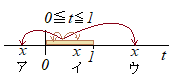 (�A)
(�A)