定積分の部分積分法

...(ＰＣ版)メニューに戻る
*** 科目 ***
数Ⅰ・Ａ数Ⅱ・Ｂ数Ⅲ 高卒・大学初年度
*** 単元 ***
複素数平面二次曲線媒介変数表示と極座標
数列の極限関数導関数不定積分定積分
行列 1次変換

※高校数学Ⅲの「定積分」について，このサイトには次の教材があります．
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください．　が現在地です．

↓定積分の基本

↓定積分の置換積分
↓同(2)

↓定積分の部分積分-現在地
↓無理関数の定積分

↓三角関数の定積分
↓三角関数（絶対値付き）の定積分
↓limΣと定積分（区分求積法）
↓同(2)入試問題

↓閉曲線で囲まれた図形の面積
↓同(2)媒介変数
↓同(3)

↓定積分の漸化式

↓体積,表面積
↓曲線の長さ

↓定積分で定義される関数

応用問題

*** 数学Ⅱ（多項式まで） ***

定積分

同(3)

面積

*** 高卒向け ***

広義積分

重積分

== 定積分の部分積分法 ==
○不定積分に関する部分積分の公式
$\int f(x)g\apos (x)dx=f(x)g(x)-\int f\apos (x)g(x) dx$
から定積分に関する部分積分の公式

$\int_a^b f(x)g\apos (x)dx=\Big[ f(x)g(x)\Big]_a^b-\int_a^b f\apos (x)g(x) dx$

が導かれる．

（詳細）
　積の微分法の公式
$\left{ f(x)g(x)\right}\apos=f\apos (x)g(x)+ f(x)g(x)\apos$
の両辺を区間a≦x≦bにおいて積分すると
　左辺の $\left{ f(x)g(x)\right}\apos$ の１つの原始関数は $f(x)g(x)$ だから
　左辺は $\Big[ f(x)g(x)\Big]_a^b$ になる．
　右辺は
$\int_a^b f\apos(x)g(x)dx + \int_a^b f(x)g\apos(x) dx$
したがって
$\Big[ f(x)g(x)\Big]_a^b=\int_a^b f\apos(x)g(x)dx + \int_a^b f(x)g\apos(x) dx$
移項すると，定積分に関する部分積分の公式が得られる．
$\int_a^b f(x)g\apos (x)dx=\Big[ f(x)g(x)\Big]_a^b- \int_a^b f\apos (x)g(x) dx$

※f' (x)g(x)とf(x)g'(x)はどちらが左辺でどちらが右辺でもよい．すなわち，次の式でもよい．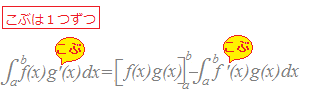
$\int_a^b f\apos (x)g(x)dx=\Big[ f(x)g(x)\Big]_a^b- \int_a^b f(x)g\apos (x) dx$

【例】
$\int_0^1 xe^x dx$
の値を求めてください．

（解答）

f(x)=x	微分する→	f '(x)=1
g(x)=ex	←積分する	g'(x)=ex

x=f(x)
ex=g'(x)
とおいて，左辺が
$\int_{0}^{1} f(x)g\apos (x)dx$
になっているものとして公式を適用する．（左辺は表の水色背景色の組だとする）
　表のように，あらかじめf(x)を微分したものf '(x)
及びg'(x)を積分したものg(x)も求めておく．
$\int_a^b f(x)g\apos (x)dx=\Big[ f(x)g(x)\Big]_a^b-\int_a^b f\apos (x)g(x) dx$
に当てはめると
$\int_0^1 xe^xdx=\Big[xe^x \Big]-\int_0^1 e^x dx$
$=(e-0)-\Big[e^x \Big]_0^1=e-(e-1)=1$ …（答）

【問題】　次の空欄を埋めなさい。

空欄にはスペースを使わずに半角の「アルファベット小文字または数字」だけを使用するものとします．

(1)

π−2∫0wwwx sinx dx

x , cosx

(2)

e∫1wwwx log x dx

logx , x , 4

(3)

e∫1wwwlog x dx

logx , x

(4)

2∫1www(x−1)(x−2)2 dx

3 , 12

(5)

π∫0wwwex sin x dx

◇考え方◇　直接的には値が求まらないとき，= Iとおいて I の方程式を解く．
　I = (···)−I　→ I = .

(･･･)2nnnn

　I = (･･･) + I型だけは不可．それ以外は，I = (･･･) ± kI 型になればすべて求まる．
※ 1回の部分積分で自分自身 I が登場しなければ，部分積分を２回行う．
(ただし，ある関数を上げて下げると何も残らないので注意．上げるなら2回上げること．)
───────────── ( )は左辺の初めの形

下げる：( f ) = sin x　→ f' = cos x
　　　　g = ex ← (g') = ex：上げる

─────────────
π∫0wwwexsinx dx=[nex −π∫0wwwex dx

=0−π∫0wwwexcosx dx

─────────────
( )は左辺の初めの形

下げる：(p) = cos x　→ p' =−sin x

　　　　q = ex ← (q') = ex：上げる

─────────────
=−([nex cos x + π∫0wwwex sin x dx )

=−(−eπ−)−π∫0wwwex sin x dx

I = eπ + 1−I

I = .

eπ+12nnnn

sinx , cosx , 1

(6)

e∫1www(log x)2 dx

x , 2 , e

［注］直前にPC版から入られた場合は，自動転送でスマホ版に来ていますので，ブラウザの［戻るキー］では戻れません（堂々巡りになる）．下記のリンクを使ってメニューに戻ってください．

...（携帯版）メニューに戻る

...（PC版）メニューに戻る

■このサイト内のGoogle検索■

△このページの先頭に戻る△【アンケート送信】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．

○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）

質問に対する回答の中学版はこの頁，高校版はこの頁にあります