�����ǂ�
��∀�`����ɔ�]�`�l�̊��z�`∅♥
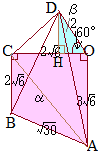
�@����������ȏ����x���̊�{���ł��D���̖��ł͎��̊Ԃō����o�Ȃ��̂ŁC�m���ɓ��_�ł���悤�ɂ��܂��傤�D
(1)
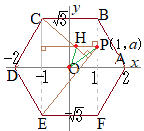
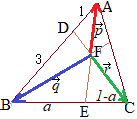
��OAB�͐��O�p�`�ł��邩��
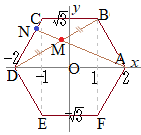
) \( \displaystyle \rm{B}(1,\hspace{2px}\sqrt{3}) \)→�A,�C
OA=OD \( \displaystyle \rm{B}(1,\hspace{2px}\sqrt{3}) \)→�A,�C
OA=OD�ł��邩��
D(−2, 0)→�E
(2)
,\hspace{2}D(-2,\hspace{2}0)) \( \displaystyle \rm{B}(1,\hspace{2px}\sqrt{3}),\hspace{2px}\rm{D}(-2,\hspace{2px}0) \) \( \displaystyle \rm{B}(1,\hspace{2px}\sqrt{3}),\hspace{2px}\rm{D}(-2,\hspace{2px}0) \)�̒��_ M�̍��W��
=(-\frac{1}{2},\hspace{2}\frac{\sqrt{3}}{2})) \( \displaystyle (\frac{1-2}{2},\hspace{2px}\frac{\sqrt{3}+ 0}{2})=(-\frac{1}{2},\hspace{2px}\frac{\sqrt{3}}{2}) \) \( \displaystyle (\frac{1-2}{2},\hspace{2px}\frac{\sqrt{3}+ 0}{2})=(-\frac{1}{2},\hspace{2px}\frac{\sqrt{3}}{2}) \)
������
=(-\frac{5}{2},\hspace{2}\frac{\sqrt{3}}{2})) \( \displaystyle \overrightarrow{\rm{AM}}=(-\frac{1}{2}-2,\hspace{2px}\frac{\sqrt{3}}{2}-0)=(-\frac{5}{2},\hspace{2px}\frac{\sqrt{3}}{2}) \)→�G,�I,�J,�L (#1) \( \displaystyle \overrightarrow{\rm{AM}}=(-\frac{1}{2}-2,\hspace{2px}\frac{\sqrt{3}}{2}-0)=(-\frac{5}{2},\hspace{2px}\frac{\sqrt{3}}{2}) \)→�G,�I,�J,�L (#1)
,\hspace{2}D(-2,\hspace{2}0)) \( \displaystyle \rm{C}(-1,\hspace{2px}\sqrt{3}),\hspace{2px}\rm{D}(-2,\hspace{2px}0) \) \( \displaystyle \rm{C}(-1,\hspace{2px}\sqrt{3}),\hspace{2px}\rm{D}(-2,\hspace{2px}0) \)������
) \( \displaystyle \overrightarrow{\rm{DC}}=(1,\hspace{2px}\sqrt{3}) \)→�N,�P (#2) \( \displaystyle \overrightarrow{\rm{DC}}=(1,\hspace{2px}\sqrt{3}) \)→�N,�P (#2)
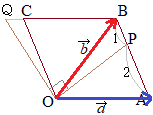
(#1)(#2)��  \( \displaystyle \overrightarrow{\rm{OA}}+ r\overrightarrow{\rm{AM}}=\overrightarrow{\rm{OD}}+ s\overrightarrow{\rm{DC}} \) \( \displaystyle \overrightarrow{\rm{OA}}+ r\overrightarrow{\rm{AM}}=\overrightarrow{\rm{OD}}+ s\overrightarrow{\rm{DC}} \)�ɑ�������
%2B r(-\frac{5}{2},\hspace{2}\frac{\sqrt{3}}{2})=(-2,\hspace{2}0)%2B s(1,\hspace{2}\sqrt{3})) \( \displaystyle (2,\hspace{2px}0)+ r(-\frac{5}{2},\hspace{2px}\frac{\sqrt{3}}{2})=(-2,\hspace{2px}0)+ s(1,\hspace{2px}\sqrt{3}) \)
x, y \( \displaystyle (2,\hspace{2px}0)+ r(-\frac{5}{2},\hspace{2px}\frac{\sqrt{3}}{2})=(-2,\hspace{2px}0)+ s(1,\hspace{2px}\sqrt{3}) \)
x, y�����ɕ������

 \( \displaystyle 2\!-\!\frac{5}{2}r\!\!-2\!+\! s\!\Longrightarrow\! 4\!-\!5r\!=\!-\!4\!+\! 2s \)���(#3) \( \displaystyle 2\!-\!\frac{5}{2}r\!\!-2\!+\! s\!\Longrightarrow\! 4\!-\!5r\!=\!-\!4\!+\! 2s \)���(#3)
 \( \displaystyle \frac{\sqrt{3}}{2}r=\sqrt{3}s\Longrightarrow r=2s \)���(#4) \( \displaystyle \frac{\sqrt{3}}{2}r=\sqrt{3}s\Longrightarrow r=2s \)���(#4)
(#4)��(#3)�ɑ��
4−10s=−4+2s
12s=8
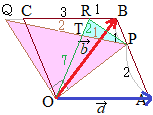
 \( \displaystyle s=\frac{2}{3} \)→�V,�X \( \displaystyle s=\frac{2}{3} \)→�V,�X
 \( \displaystyle r=\frac{4}{3} \)→�R,�T \( \displaystyle r=\frac{4}{3} \)→�R,�T
�����
 \( \displaystyle \overrightarrow{\rm{ON}}=\overrightarrow{\rm{OA}}+ r\overrightarrow{\rm{AM}} \) \( \displaystyle \overrightarrow{\rm{ON}}=\overrightarrow{\rm{OA}}+ r\overrightarrow{\rm{AM}} \)
%2B\frac{4}{3}(-\frac{5}{2},\hspace{2}\frac{\sqrt{3}}{2}) ) \( \displaystyle =(2,\hspace{2px}0)+\frac{4}{3}(-\frac{5}{2},\hspace{2px}\frac{\sqrt{3}}{2}) \) \( \displaystyle =(2,\hspace{2px}0)+\frac{4}{3}(-\frac{5}{2},\hspace{2px}\frac{\sqrt{3}}{2}) \)
%2B(-\frac{10}{3},\hspace{2}\frac{2\sqrt{3}}{3}) ) \( \displaystyle =(2,\hspace{2px}0)+(-\frac{10}{3},\hspace{2px}\frac{2\sqrt{3}}{3}) \) \( \displaystyle =(2,\hspace{2px}0)+(-\frac{10}{3},\hspace{2px}\frac{2\sqrt{3}}{3}) \)
 ) \( \displaystyle =(-\frac{4}{3},\hspace{2px}\frac{2\sqrt{3}}{3}) \)→�Z,�\,�^,�`,�c
��������B���� \( \displaystyle =(-\frac{4}{3},\hspace{2px}\frac{2\sqrt{3}}{3}) \)→�Z,�\,�^,�`,�c
��������B����
|
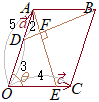 (1)
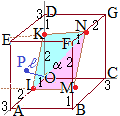
(1)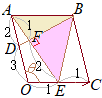 �@�E�}�ɂ����āC�O�p�`
�@�E�}�ɂ����āC�O�p�`
 (1)
(1)
 (1)
(1) (3)
(3) (1)
(1)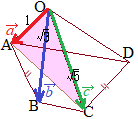 (1)
(1)


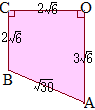 ������
������