← PC用は別頁
|
■dx の形（a>0）
被積分関数（積分記号の中にある関数）が
の形をしている場合，三角関数の相互関係の公式 1−sin2θ=cos2θ を利用することにより，置換積分で解けます． すなわち，x=sinθとおくことにより， ==±cosθ（符号は選ぶ） になり，次のように積分変数も変換すれば問題が解決します． =cosθ → dx=cosθ dθ となっている場合は，上記の変形を少しだけ変えてx=asinθとおくことにより， = =a (a>0) =±acosθ（符号は選ぶ） になります．積分変数の変換は係数が変わるだけです． =acosθ → dx=acosθ dθ ※ この変換は，x=cosθとおいてもでき，が分母にある場合でもできます． |
||||||||||||||||
|
なお，次の形の定積分については，a2−x2=tとおく置換積分により，速攻で解くことができます． x dx (a>0)
a2−x2=tとおくと
dx (a>0)
=−2x → dx=−dt x dx=−xdt =− tdt=−t=
a2−x2=tとおくと
=−2x → dx=−dt dx=− = t−dt=2t=2a |
|
【例１】
（解答）dxの値を求めてください． x=sinθとおく．（次の区間を使うとcosθ≧0となる）
積分変数は =cosθ → dx=cosθ dθ dx=cosθcosθ dθ=I 三角関数の半角公式（２倍角公式）により cos2θ=(1+cos2θ) 
だからI= (1+cos2θ)dθ =θ+= |
||||||||
|
【例２】
（解答）dxの値を求めてください． x=2sinθとおく．（次の区間を使うとcosθ≧0となる）
積分変数は =2cosθ → dx=2cosθ dθ dx=4cos2θ dθ =2 (1+cos2θ)dθ =2θ+=−  |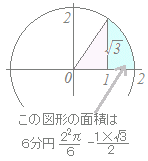
||||||||
|
【例３】
（解答）の値を求めてください． x=3sinθとおく．（次の区間を使うとcosθ≧0となる）
積分変数は =3cosθ → dx=3cosθ dθ = 3cosθ dθ = dθ =θ= |
||||||||
|
【例４】
（解答）2x dxの値を求めてください． 4−x2=tとおくと
=−2x → dx=−dt 2x dx=−2xdt = tdt=t=  |
|
次の定積分の値を求めてください．
※正しい選択肢の番号をクリックしてください．
なお，暗算ではできませんので，別途計算用紙と筆記用具が必要です． |
||||||||
|
x=3sinθとおく．（次の区間を使うとcosθ≧0となる）
積分変数は =3cosθ → dx=3cosθ dθ dx= 3cosθ·3cosθ dθ =9 cos2θ dθ=9 (1+cos2θ)dθ
=θ+=(−(−))= → 2
|
||||||||
|
x=sinθとおく．（次の区間を使うとcosθ≧0となる）
積分変数は =cosθ → dx=cosθ dθ = cosθ dθ = dθ
=θ=
→ 2
|
||||||||
|
2−x2=tとおくと
=−2x → dx=−dt dx=−dt = t−dt=2t
=2(−1)
→ 2
|
|
【例５】
（解答）dxの値を求めてください．
dx
だけでなく，
dxの形になっているものや，
dx (p>0)の形でも，
dxの形に変形できるものは，
ここまでと同様の変形で，置換積分ができます．
2x−x2=1−(x−1)2だからdx= dx
以下の解説が分かりにくい場合は，一旦x−1=tとおいて，簡単な式に直してから，再度t=sinθの置換積分を行えばよいが，ある程度慣れてきたら，次のように一回の置換で行ってもよい．
x−1=sinθとおく．（次の区間を使うとcosθ≧0となる）
積分変数は =cosθ → dx=cosθ dθ cosθcosθ dθ=cos2θ dθ = (+)dθ =+= |
||||||||
|
3+2x−x2=4−(x−1)2だから
x−1=2sinθとおく．（次の区間を使うとcosθ≧0となる）
==2cosθ 積分変数は =2cosθ → dx=2cosθ dθ dθ=dθ
=θ=
→ 1
（参考）
a<bのとき，次の公式が成り立ちます． dx=(b−a)2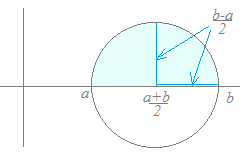 
右図の水色で示した半円の面積はπ()2÷2 =(b−a)2 ⇒この頁の例１，例２，問題１，例５の検算に使えます． |
|
次の形の不定積分（代入して差を求めれば定積分）は，高校の数学で「覚えるべきものと扱われていない」のが普通です．
・筆算で導くには途中経過がとても長くなる．
理数系の大学生で必要な場面があれば，
・覚えていればできるが，覚えていないと難しい． ・以上の結果，この種の問題を出題すると，数学的な考え方や計算力を問うよりも単なる暗記力を問う側面が強くなる．
「公式を見ながら使えればよい」
ぐらいの考え方でよいと思う．「コンピュータを使って計算できたらよい」 そのためには，
公式は覚えなくてもよいが，
は覚えておく必要がある．
「そういう公式がある」ということ
次の公式においてAは，負の数でもよいが，その場合は根号内が０以上になる区間でのみ積分が定義できる．A=0のときは，式の形が変わる（根号がはずれる）のでA≠0の場合の公式となっている．
dx=log|x+|++C…(*1)
=log|x+|+C…(*2) |
|
（公式を適用した場合）
dx=log|x+|+ で求めた結果 ⇒
（別ルートで検算した場合）
dxを数値積分で求めた値 台形公式（100000分割）の場合 ⇒
※（参考） wxMaxima（インストール方法，使い方の例）を使えば，公式(*1)の計算は，例えば次のようになります．
○1 dxを求めるには
→ integrate(sqrt(x^2+1), x, 0, 1); と入力する → 結果はと返される （双曲線関数の逆関数で表される） ○2 dxを求めるには → integrate(x^2+2, x, 1, 3); と入力する → これもかなり複雑な逆双曲線関数が返される ○1，○2とも結果を小数で求めることもできる．
（公式を適用した場合）
=log|x+| で求めた結果 ⇒
（別ルートで検算した場合）
を数値積分で求めた値 台形公式（100000分割）の場合 ⇒
※（参考）
wxMaximaを使って，公式(*2)の計算を行うこともできます． |
|
［注］直前にPC版から入られた場合は，自動転送でスマホ版に来ていますので，ブラウザの［戻るキー］では戻れません（堂々巡りになる）．下記のリンクを使ってメニューに戻ってください．
 ...（携帯版）メニューに戻る...（PC版）メニューに戻る |
定積分