← PC用は別頁
|
*** 蟄ｦ蟷ｴ *** 荳ｭ蟄ｦ�大ｹｴ荳ｭ蟄ｦ�貞ｹｴ荳ｭ蟄ｦ�灘ｹｴ *** 蜊伜� *** 蠑上�螻暮幕蝗�謨ｰ蛻�ｧ｣邏�謨ｰ繝ｻ邏�蝗�謨ｰ蛻�ｧ｣蟷ｳ譁ｹ譬ｹ �呈ｬ｡譁ｹ遞句ｼ�荳牙ｹｳ譁ｹ縺ｮ螳夂炊�呈ｬ｡髢｢謨ｰ蟷ｳ陦檎ｷ壹�逶ｸ莨ｼ 窶ｻ荳ｭ蟄ｦ�灘ｹｴ逕溷髄縺�縲御ｸ牙ｹｳ譁ｹ縺ｮ螳夂炊縲�縺ｫ縺､縺�※�後％縺ｮ繧ｵ繧､繝医↓縺ｯ谺｡縺ｮ謨呎攝縺後≠繧翫∪縺呻ｼ� 縺薙�鬆√∈Google繧ШAHOO ! 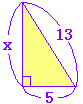縺ｪ縺ｩ縺ｮ讀懃ｴ｢縺九ｉ逶ｴ謗･譚･縺ｦ縺励∪縺｣縺溘�縺ｧ縲悟燕謠舌→縺ｪ縺｣縺ｦ縺�ｋ蜀�ｮｹ縺悟�縺九ｉ縺ｪ縺�阪→縺�≧蝣ｴ蜷医ｄ縲後％縺ｮ鬆√�蛻�°縺｣縺溘′繧ゅ▲縺ｨ蠢懃畑蝠城｡後ｒ隕九◆縺�阪→縺�≧蝣ｴ蜷医��御ｻ悶�鬆√ｒ隕九※縺上□縺輔＞��縲 縺檎樟蝨ｨ蝨ｰ縺ｧ縺呻ｼ�  ...�域声蟶ｯ迚茨ｼ峨Γ繝九Η繝ｼ縺ｫ謌ｻ繧�...(�ｰ�｣迚�)繝｡繝九Η繝ｼ縺ｫ謌ｻ繧�===三平方の定理=== ■解説 ○次の図のｘの値は三平方の定理を１回用いて求めることができます。
|
|
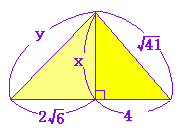
○次の図のｘ，ｙの値は三平方の定理を2回用いて求めることができます。まずｘを求め，次にｙを求めます。
|
| ■問題１ 次の各図でｘの値を求めなさい。(各々三平方の定理を１回使えばできます。) |
|
直角三角形で斜辺の長さがｘだから
x2=52+(2√6)2 x2=25+24=49 |
|
直角三角形で斜辺の長さが6だから
x2+(4√2)2=62 x2+32=36 x2=4 |
|
直角三角形で斜辺の長さがｘだから
x2=(5√2)2+(√14)2 x2=50+14=64 |
| ■問題２ 次の各図でｘ，ｙの値を求めなさい。(各々三平方の定理を2回使えばできます。) |
|
まずｘを求め、次にｙを求めます。
ｘは直角三角形の斜辺だから x2=(4√3)2+(2√13)2=48+52=100 x=10 次に，下半分の直角三角形でｘは斜辺だから
|
|
まずｘを求め、次にｙを求めます。
ｘは直角三角形の斜辺だから x2=22+(√5)2=4+5=9 x=3 次に，下半分の直角三角形で√13は斜辺だから
|
|
まずｘを求め、次にｙを求めます。
√13は直角三角形の斜辺だから (√13)2=x2+22 13=x2+4 x=3 次に，大きい方の直角三角形でｙは斜辺だから
|
|
まずｘを求め、次にｙを求めます。
xは直角三角形の斜辺だから x2=32+42=25 x=5 次に，もう一つの直角三角形でもｘは斜辺だから
|
|
...（携帯版）メニューに戻る...メニューに戻る |
| 鬯ｮ�ｫ�ｽ�ｨ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ鬯ｩ謳ｾ�ｽ�ｵ�ｽ�ｽ�ｽ�ｺ鬯ｮ�ｦ�ｽ�ｮ髯ｷ�ｻ�ｽ�ｻ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ鬯ｩ蟷｢�ｽ�｢�ｽ�ｽ�ｽ�ｧ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｵ鬯ｩ蟷｢�ｽ�｢�ｽ�ｽ�ｽ�ｧ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�､鬯ｩ蟷｢�ｽ�｢髫ｴ荵暦ｿｽ�ｽ�ｽ�ｽ�ｺ�ｽ�ｽ�ｽ�･�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ鬯ｩ謳ｾ�ｽ�ｵ�ｽ�ｽ�ｽ�ｺ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｮGoogle鬯ｮ�ｫ�ｽ�ｶ�ｽ縺､ﾂ鬮ｫ�ｲ陝ｷ�｢�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｴ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｢鬯ｮ�ｫ�ｽ�ｨ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ |