|
※中学３年生向け「三平方の定理」について，このサイトには次の教材があります． この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください． が現在地です．  ...（携帯版）メニューに戻る...(ＰＣ版)メニューに戻る
≪２点間の距離の公式≫
○ ２点A(a, b), B(c,d)間の距離は  √(c−a)2+(d−b)2 …(1)に等しい． ○ 特に，原点O(0,0)とP(x,y)との間の距離は √x2+y2 …(2)
(*) 三平方の定理（ピタゴラスの定理）
直角三角形において斜辺の長さをc，直角と隣り合う２辺の長さをa, bとするとき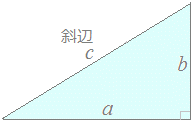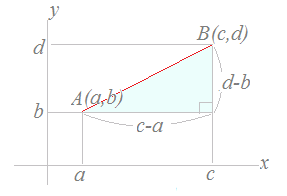  
（解説）
２点間の距離の公式は，三平方の定理から導かれます．
(1)←右の直角三角形において，横の長さは c−a，縦の長さは d−bだから， 三平方の定理(*)を使うと斜辺の長さを求めることができます． AB2=(c−a)2+(d−b)2 AB=  √(c−a)2+(d−b)2
a>cのときやb>dのときは，辺の長さは各々a−c, b−dとなって途中経過は変わりますが，結果は上の公式が使えます．
(2)←さらに，a=cのときやb=dのときは，直角三角形が「つぶれて」縦線や横線になりますが，その場合でも結果は上の公式が使えます．（参考→） 原点と点P(x,y)との間の距離は(1)式にa=0,b=0,c=x,d=yを代入すると得られます． OP= √(x−0)2+(y−0)2=√x2+y2 理論上，(1)式があれば(2)式はいらないのなら，なぜ(2)式も公式にするのか？と文句を言いたい人へ．
→公式の重要さは「適用範囲の広さ」だけではなく，「よく使う」かどうかでも決まります．「よく使う」ものはすぐ使えるようにパックにしておくと便利だということです．
→参考
a=cのときやb=dのときは，三角形が「つぶれて」縦線または横線になりますが，この場合でも公式(1)は成り立ちます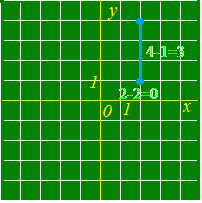．  AB=4−1=3 公式からは AB=  √(2−2)2+(4−1)2=√0+9=3となって，結果は一致します． さらに，a=cかつb=dのときは，三角形が完全に「つぶれて」１点になりますが，この場合でも公式(1)は成り立ちます． AA= √(a−a)2+(b−b)2=√0=0 |
|
例 (1) ２点A(1, 1), B(4,5)間の距離 :
x座標の差は4−1=3.
y座標の差は5−1=4. 公式(1)に当てはめると， AB= √3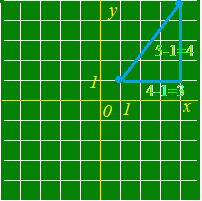2+42=√25=5
 ２点A(−3, 4), B(2, −1)間の距離 :
x座標の差は2−(−3)=5.
y座標の差は−1−4=−5. （符号がマイナスになっても２乗して使うので気にしない） 公式(1)に当てはめると， AB= √5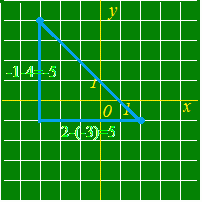2+(−5)2=√50=5√2
 原点からP(3, 2)までの距離 :
公式(2)に当てはめると，
AB= 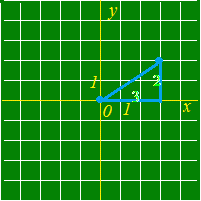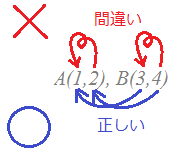√32+22=√13
  ≪よくある間違い≫• 引き算はx座標同士，y座標同士で行わなければなりません． 例えば，２点A(1, 2), B(3, 4)間の距離を求めたいとき, √(2−1)2+(4−3)2 ← ×√(3−1)2+(4−2)2 ← ○• 座標がマイナスのときに引き算の符号を間違う生徒が多い． 例えば，２点C(−5, 6), D(7, 8)間の距離を求めたいとき， √(7−5)2+(8−6)2 ← ×√(7−(−5))2+(8−6)2 ← ○ |
|
問題次の２点間の距離を求めてください． （正しいものを下の欄から選んでください．暗算では無理なので，計算用紙を使ってください．） |
|
...（携帯版）メニューに戻る...メニューに戻る |
|
■［個別の頁からの質問に対する回答］[２点間の距離の公式について／18.6.6］
地球上の２点の緯度・経度を与えて、その２点間の距離を求めたいのですが。
簡易な方法と正確な方法を教えて頂けると助かります。
■［個別の頁からの質問に対する回答］[２点間の距離の公式について／18.4.25］
＝＞［作者］：連絡ありがとう．球面三角法というキーワードで検索すると公式が出てきます．このページなど．結果を確かめるにはこのペ－ジなど わかりやすい
＝＞［作者］：連絡ありがとう． |
| ■このサイト内のGoogle検索■ |