← PC用は別頁
|
*** 陝�ｽｦ陝ｷ�ｴ *** 闕ｳ�ｭ陝�ｽｦ�ｽ螟ｧ�ｹ�ｴ闕ｳ�ｭ陝�ｽｦ�ｽ雋橸ｽｹ�ｴ闕ｳ�ｭ陝�ｽｦ�ｽ轣假ｽｹ�ｴ *** 陷贋ｼ懶ｿｽ *** 陟台ｸ奇ｿｽ陞ｻ證ｮ蟷�陜暦ｿｽ隰ｨ�ｰ陋ｻ�ｽ�ｧ�｣驍擾ｿｽ隰ｨ�ｰ郢晢ｽｻ驍擾ｿｽ陜暦ｿｽ隰ｨ�ｰ陋ｻ�ｽ�ｧ�｣陝ｷ�ｳ隴�ｽｹ隴ｬ�ｹ �ｽ蜻茨ｽｬ�｡隴�ｽｹ驕槫唱�ｼ�ｽ闕ｳ迚呻ｽｹ�ｳ隴�ｽｹ邵ｺ�ｮ陞ｳ螟らｊ�ｽ蜻茨ｽｬ�｡鬮｢�｢隰ｨ�ｰ陝ｷ�ｳ髯ｦ讙趣ｽｷ螢ｹ�ｽ騾ｶ�ｸ闔ｨ�ｼ 遯ｶ�ｻ闕ｳ�ｭ陝�ｽｦ�ｽ轣假ｽｹ�ｴ騾墓ｺｷ鬮�ｸｺ�ｽ邵ｲ蠕｡�ｸ迚呻ｽｹ�ｳ隴�ｽｹ邵ｺ�ｮ陞ｳ螟らｊ邵ｲ�ｽ邵ｺ�ｫ邵ｺ�､邵ｺ�ｽ窶ｻ�ｽ蠕鯉ｼ�ｸｺ�ｮ郢ｧ�ｵ郢ｧ�､郢晏現竊鍋ｸｺ�ｯ隹ｺ�｡邵ｺ�ｮ隰ｨ蜻取駁邵ｺ蠕娯旺郢ｧ鄙ｫ竏ｪ邵ｺ蜻ｻ�ｼ�ｽ 邵ｺ阮呻ｿｽ鬯��竏�Google郢ｧﾐｨAHOO ! 邵ｺ�ｪ邵ｺ�ｩ邵ｺ�ｮ隶諛�ｽｴ�｢邵ｺ荵晢ｽ蛾ｶ�ｴ隰暦ｽ･隴夲ｽ･邵ｺ�ｦ邵ｺ蜉ｱ竏ｪ邵ｺ�｣邵ｺ貅假ｿｽ邵ｺ�ｧ邵ｲ謔溽√隰�闊娯�邵ｺ�ｪ邵ｺ�｣邵ｺ�ｦ邵ｺ�ｽ�玖怙�ｽ�ｮ�ｹ邵ｺ謔滂ｿｽ邵ｺ荵晢ｽ臥ｸｺ�ｪ邵ｺ�ｽﾂ髦ｪ竊堤ｸｺ�ｽ竕ｧ陜｣�ｴ陷ｷ蛹ｻ��ｸｲ蠕鯉ｼ�ｸｺ�ｮ鬯���ｽ陋ｻ�ｽﾂｰ邵ｺ�｣邵ｺ貅倪ｲ郢ｧ繧�夢邵ｺ�ｨ陟｢諛�舞陜�蝓趣ｽ｡蠕鯉ｽ帝囎荵昶螺邵ｺ�ｽﾂ髦ｪ竊堤ｸｺ�ｽ竕ｧ陜｣�ｴ陷ｷ蛹ｻ�ｽ�ｽ蠕｡�ｻ謔ｶ�ｽ鬯���帝囎荵昶ｻ邵ｺ荳岩味邵ｺ霈費ｼ橸ｿｽ�ｽ邵ｲﾂ 邵ｺ讙取ｨ溯舉�ｨ陜ｨ�ｰ邵ｺ�ｧ邵ｺ蜻ｻ�ｼ�ｽ  ...�ｽ蝓溷｣ｰ陝ｶ�ｯ霑夊肩�ｼ蟲ｨﾎ鍋ｹ昜ｹ斟礼ｹ晢ｽｼ邵ｺ�ｫ隰鯉ｽｻ郢ｧ�ｽ...(�ｽ�ｰ�ｽ�｣霑夲ｿｽ)郢晢ｽ｡郢昜ｹ斟礼ｹ晢ｽｼ邵ｺ�ｫ隰鯉ｽｻ郢ｧ�ｽ■次のような直角三角形の三辺の長さについては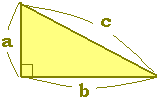，  （これを三平方の定理の逆といいます．） 一番長い辺が斜辺です． ※ 直角三角形であるかどうかを調べるには，
【要点】
小さい方の２辺を直角な２辺として，２乗の和 a2+b2 を作り，一番長い辺を斜辺として c2 を作る．
a2+b2=c2 ⇒ 直角三角形
a2+b2≠c2 ⇒ 直角三角形ではない |
|
■問題１ 次のように三角形の三辺の長さが与えられているとき，これらのうちで直角三角形となっているものを選びなさい．
（４組のうち１組が直角三角形です．）
|
|
 |
|
|
|
|
|
|
|
|
（4）
「6 , 11 , 13」 「6 , 12 , 13」 |
|
|
|
|
|
（5）
「9 , 39 , 41」 「9 , 40 , 41」 |
|
|
|
|
|
■問題２ 次のように三角形の三辺の長さが与えられているとき，これらのうちで直角三角形となっているものを選びなさい． |
|
Help
(  √5−√3)2+(√5+√3)2
=5+3−2√15 +5+3+2√15 =16=42 |
|
Help
(3
√3−1)2+(3√3+1)2
=27+1−6√3 +27+1+6√3 =56=(2 √14 )2
( √7−√2 )2+(√7+√2 )2
=7+2−2√14 +7+2+2√14 =18=(3 √2 )2
|
|
Help
(2
√3−√2 )2+(√3+2√2)2
=12+2−4√6 +3+8+4√6 =25=52 |
|
左辺は 4m2n2+m4-2m2n2+n4 右辺は m4+2m2n2+n4 だから等しい 例 m=2,n=1 を代入すると 42+32=52 となります．（このとき，3 , 4 , 5 の組がピタゴラス数） |
|
■（自由研究） 左の式を利用して,三辺の長さが整数となる直角三角形を1組見つけなさい．（上の問題にないもので答えなさい･･･ただし，このホームページでは,あまり大きな数字の計算はできないので,どの辺の長さも100以下で答えなさい．） |
|
ピタゴラス数の例（小さい方から幾つか） |
|||||
| m | n | 2mn | m2−n2 | m2+n2 | 成り立つ関係 |
| 2 | 1 | 4 | 3 | 5 | 42+32=52 |
| 3 | 1 | 6 | 8 | 10 | 62+82=102 |
| 3 | 2 | 12 | 5 | 13 | 122+52=132 |
| 4 | 1 | 8 | 15 | 17 | 82+152=172 |
| 4 | 2 | 16 | 12 | 20 | 162+122=202 |
| 4 | 3 | 24 | 7 | 25 | 242+72=252 |
| 5 | 1 | 10 | 24 | 26 | 102+242=262 |
| 5 | 2 | 20 | 21 | 29 | 202+212=292 |
| 5 | 3 | 30 | 16 | 34 | 302+162=342 |
| 5 | 4 | 40 | 9 | 41 | 402+92=412 |
| 6 | 1 | 12 | 35 | 37 | 122+352=372 |
| 6 | 2 | 24 | 32 | 40 | 242+322=402 |
| 6 | 3 | 36 | 27 | 45 | 362+272=452 |
| 6 | 4 | 48 | 20 | 52 | 482+202=522 |
| 6 | 5 | 60 | 11 | 61 | 602+112=612 |
| 7 | 1 | 14 | 48 | 50 | 142+482=502 |
| 7 | 2 | 28 | 45 | 53 | 282+452=532 |
| 7 | 3 | 42 | 40 | 58 | 422+402=582 |
| 7 | 4 | 56 | 33 | 65 | 562+332=652 |
| 7 | 5 | 70 | 24 | 74 | 702+242=742 |
| 7 | 6 | 84 | 13 | 85 | 842+132=852 |
| 8 | 1 | 16 | 63 | 65 | 162+632=652 |
| 8 | 2 | 32 | 60 | 68 | 322+602=682 |
| 8 | 3 | 48 | 55 | 73 | 482+552=732 |
| 8 | 4 | 64 | 48 | 80 | 642+482=802 |
| 8 | 5 | 80 | 39 | 89 | 802+392=892 |
| 8 | 6 | 96 | 28 | 100 | 962+282=1002 |
| 8 | 7 | 112 | 15 | 113 | 1122+152=1132 |
| ··· | ··· | ··· | ··· | ··· | ··· |
|
...（携帯版）メニューに戻る...メニューに戻る |
| 鬯ｯ�ｯ�ｽ�ｮ�ｽ�ｽ�ｽ�ｫ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｨ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ鬯ｯ�ｯ�ｽ�ｩ髫ｰ�ｳ�ｽ�ｾ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｵ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｺ鬯ｯ�ｯ�ｽ�ｮ�ｽ�ｽ�ｽ�ｦ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｮ鬯ｮ�ｯ�ｽ�ｷ�ｽ�ｽ�ｽ�ｻ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｻ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ鬯ｯ�ｯ�ｽ�ｩ髯晢ｽｷ�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｧ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｵ鬯ｯ�ｯ�ｽ�ｩ髯晢ｽｷ�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｧ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�､鬯ｯ�ｯ�ｽ�ｩ髯晢ｽｷ�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｢鬯ｮ�ｫ�ｽ�ｴ髣包ｽｵ隴会ｽｦ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｺ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�･�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ鬯ｯ�ｯ�ｽ�ｩ髫ｰ�ｳ�ｽ�ｾ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｵ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｺ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｮGoogle鬯ｯ�ｯ�ｽ�ｮ�ｽ�ｽ�ｽ�ｫ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｶ�ｽ�ｽ�ｽ�ｽ驍ｵ�ｺ�ｽ�､�ｽ縺､ﾂ鬯ｯ�ｮ�ｽ�ｫ�ｽ�ｽ�ｽ�ｲ鬮ｯ譎｢�ｽ�ｷ�ｽ�ｽ�ｽ�｢�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｴ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｢鬯ｯ�ｯ�ｽ�ｮ�ｽ�ｽ�ｽ�ｫ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｨ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ |