■ 三平方の定理の逆
《解説》
■次のような直角三角形の三辺の長さについては，
a2+b2=c2
が成り立ちます．（これを三平方の定理といいます．）
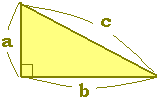■逆に，三辺の長さについて，
a2+b2=c2
が成り立つとき，その三角形は直角三角形です．
（これを三平方の定理の逆といいます．）
一番長い辺が斜辺です． |
※ 直角三角形であるかどうかを調べるには，
a2+b2 と c2 を比較してみれば分かります．
例
三辺の長さが 3,4,5 の三角形が直角三角形であるかどうか調べるには，
5 が一番長い辺だから，
42+52=?=32
52+32=?=42
が成り立つ可能性はないから，調べる必要はない．
32+42 =?= 52
が成り立つかどうか調べればよい．
32+42=9+16=25 , 52=25 だから，32+42=52
ゆえに，直角三角形である．
例
三辺の長さが 4 , 5 , 6 の三角形が直角三角形であるかどうか調べるには，
42+52≠62 により，直角三角形ではないといえる．
|
【要点】
小さい方の２辺を直角な２辺として，２乗の和 a2+b2 を作り， 一番長い辺を斜辺として c2 を作る．
これらが等しいとき ⇒ 直角三角形（他の組合せで，a2+b2=c2 となることはない．）
これらが等しくないとき ⇒ 直角三角形ではない
|
■ 問題 次のように三角形の三辺の長さが与えられているとき，これらのうちで直角三角形となっているものを選びなさい．
（４組のうち１組が直角三角形です．）
|
（1）
「3 , 3 , 4」 「3 , 4 , 4」 「3 , 4 , 5」 「3 , 4 , 6」
|
|
|
|
| （2）
「1 , 2 , 2」 「1 , 2 , 」 「1 , 2 , 」 「1 , 2 , 」
|
|
|
|
| （3）
「1 , , 」 「1 , , 」 「1 , , 2」
「1 ,
, 3」
|
|
|
|
| （4）
「5 , 11 , 12」 「5 , 12 , 13」 「6 , 11 , 13」 「6 , 12 , 13」
|
|
|
|
| （5）
「8 , 39 , 41」 「8 , 40 , 41」 「9 , 39 , 41」 「9 , 40 , 41」
|
|
|
|
■ 問題 次のように三角形の三辺の長さが与えられているとき，これらのうちで直角三角形となっているものを選びなさい．（ややむずかしい）
(1)
「
−
,
+
,
」
「
−
,
+
,
2
」
「
−
,
+
,
4
」
「
−
,
+
,
8
」
|
|
Help
(−)2+(+)2
=5+3−2 +5+3+2 =16
=42
|
|
|
(2)
「3
−1
,
3
+1
, 2
」
「3
−1
,
3
+1
, 6
」
「−
,
+
,
2
」
「−
,
+
,
9
」
|
|
Help
(3−1)2+(3+1)2
=27+1−6 +27+1+6 =56
=(2 )2
(− )2+(+ )2
=7+2−2 +7+2+2 =18
=(3 )2
|
|
|
(3)
「2
−
,
+2
, 2
」
「2
−
,
+2
, 2
」
「2
−
,
+2
, 5
」
「2
−
,
+2
, 3
」
|
|
Help
(2− )2+(+2)2
=12+2−4 +3+8+4 =25
=52
|
|
|
■ ピタゴラス数の問題
○ 次の式の m , n に適当な正の整数(ただし m>n)を入れれば,「三辺の長さが整数となる直角三角形」ができます． （正の整数で三平方の定理を満たすものは，ピタゴラス数と呼ばれます．）
(2mn)2+(m2-n2)2=(m2+n2)2
左辺は 4m2n2+m4-2m2n2+n4
右辺は m4+2m2n2+n4 だから等しい
例 m=2,n=1 を代入すると 42+32=52 となります．（このとき，3 , 4 , 5 の組がピタゴラス数）
|
■ 問題
左の式を利用して,三辺の長さが整数となる直角三角形を1組見つけなさい．（上の問題にないもので答えなさい･･･ただし，このホームページでは,あまり大きな数字の計算はできないので,どの辺の長さも100以下で答えなさい．）
|
|
...メニューに戻る