|
���i���Δ�j���̑̐ςƕ\�ʐ� �@�ȉ��̋��ނł́C�����̌����ȏؖ��ł��Ȃ��C�P�Ȃ�ۈËL�ł��Ȃ��C�����̂Ȃ��͈͂ŊȒP�Ȑ�����t���Ă����̌������g����悤�ɂȂ邱�Ƃ�ڎw���D  ���@�~�a�̉��ɂP��]���Ăł��闧�̂����Ƃ����D�u���v�Ƃ����Ƃ��͒��g�̋l�܂������́i���́j���l���C���̕\�ʂ������l����Ƃ��́u���ʁv�Ƃ����D
���@�~�a�̉��ɂP��]���Ăł��闧�̂����Ƃ����D�u���v�Ƃ����Ƃ��͒��g�̋l�܂������́i���́j���l���C���̕\�ʂ������l����Ƃ��́u���ʁv�Ƃ����D���@�싅�C�e�j�X�C�T�b�J�[�C�o���[�{�[���ȂǑ����́u���Z�v�Ŏg����{�[���́C�\�ʂ̂킸���Ȗ͗l�̈Ⴂ��ʂƂ�����̌`�����Ă���D�i���O�r�[�C�A�����J���t�b�g�{�[���̃{�[���C���Ȃǂ̌`�͋��ł͂Ȃ��D�j�n���́C�ԓ��̂����肪�����ӂ����ł��邪�C�قڋ��̌`�ɂȂ��Ă���ƍl���Ă悢�D 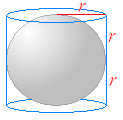 ���@�M���V���̃A���L���f�X�̎��ォ��C�~���ɂ����ۂ���鋅�̑̐ς́C�~���̑̐ς̂R���̂Q�ɂȂ邱�Ƃ��m���Ă����D���̂��Ƃ͉~���ɐ������Ă����C���߂Ă��ӂ�鐅�̕��ʂׂ�Ɗm���߂邱�Ƃ��ł���D
���@�M���V���̃A���L���f�X�̎��ォ��C�~���ɂ����ۂ���鋅�̑̐ς́C�~���̑̐ς̂R���̂Q�ɂȂ邱�Ƃ��m���Ă����D���̂��Ƃ͉~���ɐ������Ă����C���߂Ă��ӂ�鐅�̕��ʂׂ�Ɗm���߂邱�Ƃ��ł���D���@�E�}�̂悤�ɋ��̊O���ɂ҂�����ڂ���~�������ƁC���̒�ʂ͔��a�� r �̉~�C������ 2r �ɂȂ邩��C�~���̑̐ς� ��r2�~2r=2��r3 �@���̑̐ς́C���̂R���̂Q������
�m���̑̐ρn
�@���a r �̋��̑̐ς� V �ŕ\�킷�� ���@�u�g(3)�̏�ɐS�z(4��)����( r )��( 3 )�v�Ƃ����o�������L���D  ���@�ʏ�C�����ۈËL�Ƃ����w�K���@���������̂́C��肪�ς���������Ȃ��Ȃ邩��ł��邪�C���Z���wIII�Ŏ��ۂɔ����ϕ����K���Ƃ��ȊO�͋���ό`�����`�i���Ƃ��Ή�]�ȉ~�́F�E�}�j�Ȃǂ̑̐ς�����邱�Ƃ͂Ȃ��D������C���̑̐ςɂ��Ă͏�̌������o���邾���ł悢�D ���@�ʏ�C�����ۈËL�Ƃ����w�K���@���������̂́C��肪�ς���������Ȃ��Ȃ邩��ł��邪�C���Z���wIII�Ŏ��ۂɔ����ϕ����K���Ƃ��ȊO�͋���ό`�����`�i���Ƃ��Ή�]�ȉ~�́F�E�}�j�Ȃǂ̑̐ς�����邱�Ƃ͂Ȃ��D������C���̑̐ςɂ��Ă͏�̌������o���邾���ł悢�D�m���1�n�@���a 2 �̋��̑̐ς����߂Ȃ����D �i���āj  �m���2�n�@���a 4 �̋��̏㔼���̑̐ς����߂Ȃ����D �m���2�n�@���a 4 �̋��̏㔼���̑̐ς����߂Ȃ����D�i���āj
�m���1�n
(1)�@���a 3 �̋��̑̐ς����߂Ȃ����D (2)�@�u���a�v 10(cm) �̋��̑̐ς����߂Ȃ����D ���a�� 10(cm) �����甼�a�� 5(cm) (3)�@�f���`�̔��a���f���a�̔��a�̂Q�{�ł���Ƃ��C�f���`�̑̐ς͘f���a�̑̐ς̉��{���D �f���a�̔��a�� r �Ƃ����ƁC���̑̐ς� ���ɁC�f���`�̔��a�� 2r �ƂȂ邩��C ���̑̐ς� �i�u�̐ϔ�͑�����̂R���v���g���C�����䂪1�F2������̐ϔ��13�F23=1:8�@�����܂�D�j |
|
�m���̕\�ʐρn
�i����j�@���a r �̋��̕\�ʐς� S �ŕ\�킷�� 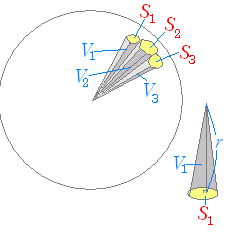 ���@��ʐς� S �C������ h �Ƃ���Ƃ��C�O�p���C�l�p���C����C�~���̑̐ς͂������ ���@��ʐς� S �C������ h �Ƃ���Ƃ��C�O�p���C�l�p���C����C�~���̑̐ς͂�������ɂȂ�D �@����𗘗p���ċ��̑̐ς��~���i�p���j�̑̐ςŕ\�킷���Ƃ��ł���D ���@�E�}�̂悤�ɋ��̒��S���狅�ʂɌ������āu�n�`�̑��v�̂悤�ȉ~���ɕ�����D���̂Ƃ��C������ꂽ���ꂼ��̉~���͉E�}���ɕ`�����悤�ɁC���ʂ̈ꕔ�����~���̒�ʂɂȂ�C���̔��a���~���̍����ɑΉ�����D�~���Ɖ~������ׂ�Ƌ��̕\�ʂɌ��Ԃ��ł��Ă��܂��悤�Ɏv����������Ȃ����C���ۂɂ͐��m�ȉ~���łȂ��Ă��C�O�p���C�l�p���C�܊p���C����C�~���̂�������̐ς́i��ʐρj�~�i�����j���R�ɂȂ�̂ŁC���̕\�ʂł̌`�ɂ͂������Ȃ��Ă��悢�D�܂��C�E�}�ł͉~���̍����Ƃ������͕���̒����� ������ r �ɂȂ�̂ł͂Ȃ����Ǝv���l�����邩������Ȃ����C������������D�ׂ���������ƕ���̒����Ɖ~���̍������قƂ�Ǔ������Ȃ�̂ŁC�ǂ���� r �Ƃ��Ă悢�D ���@�e�X�̉~���i�p���j�̑̐ςƒ�ʐς̊Ԃɂ́C���̊W�����藧�D … … … �@�~����S���W�߂�Ƌ��ɂȂ�C��ʂ�S���W�߂�Ƌ��ʂɂȂ邩�� �@�䂦�ɁC ���@���̑̐ς� (1)(2)��� �@����� S=4��r2 �ɂȂ�D___�ؖ��I�聡 �m���3�n�@���a 2 �̋��̕\�ʐς����߂Ȃ����D �i���āj S=4���~22=16�� …�i���j 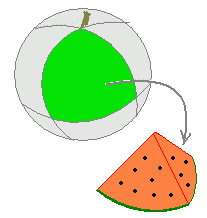 �m���4�n�@���a 10(cm) �̃X�C�J���E�}�̂悤�ɏc�C���C�㉺�ɂQ�������ĂW�l�ɕ�����Ƃ��C�P�l���̃X�C�J�̕\�ʐς����߂Ȃ����D �m���4�n�@���a 10(cm) �̃X�C�J���E�}�̂悤�ɏc�C���C�㉺�ɂQ�������ĂW�l�ɕ�����Ƃ��C�P�l���̃X�C�J�̕\�ʐς����߂Ȃ����D�i���āj �\�ʂ̗ΐF�̕����́C���̕\�ʂ̂W����1������ �@�~4���~102=50�� ����̐ԐF�̕����́C�~�̖ʐς̂S����1��3���邩�� �@�~���~102�~3=�� �\�ʐς́C50��+�� =��=125��(cm2)�@…�i���j |
|
���@���̕\�ʐ�S�͉~�̖ʐ���r2�̂S�{�ɂȂ�D�i���ɂ��ꂢ�ȊW�j ���@���Z���wIII�Ŕ������K���C�̐� �m���2�n (1)�@�@���a 5 �̋��̕\�ʐς����߂Ȃ����D (2)�@�@���a 3 �̋��̕\�ʐς����߂Ȃ����D (3)�@�@���`�̔��a�����a�̔��a�̂Q�{�ł���Ƃ��C���̋߂Ȃ����D 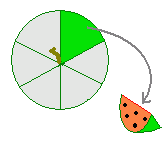 (4)�@�@���a 6(cm) �̃X�C�J���E�}�̂悤�ɏc�ɂU�������ĂU�l�ɕ�����Ƃ��C�P�l���̃X�C�J�̕\�ʐς����߂Ȃ����D (4)�@�@���a 6(cm) �̃X�C�J���E�}�̂悤�ɏc�ɂU�������ĂU�l�ɕ�����Ƃ��C�P�l���̃X�C�J�̕\�ʐς����߂Ȃ����D |
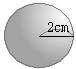 �@�E�̐}�̂悤�ɁC���a��2cm�̋�������܂��B���̋��̕\�ʐς����߂Ȃ����B
�@�E�̐}�̂悤�ɁC���a��2cm�̋�������܂��B���̋��̕\�ʐς����߂Ȃ����B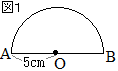 �@�}�P�̔��~���C����AB����]�̎��Ƃ���1��]�����Ăł��闧�̂̕\�ʐς����߂Ȃ����B�������C�~������
�@�}�P�̔��~���C����AB����]�̎��Ƃ���1��]�����Ăł��闧�̂̕\�ʐς����߂Ȃ����B�������C�~������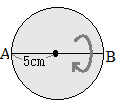 �@1��]������ƁC�E�}�̂悤�ȋ��ɂȂ�D
�@1��]������ƁC�E�}�̂悤�ȋ��ɂȂ�D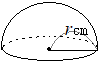 �@�E�̐}�͔��a
�@�E�̐}�͔��a