|
■(例題対比)球の体積と表面積 ※ 球の体積・表面積の公式のきっちりとした証明は,高校数学III(高3)で微分積分を用いて行われるが,それまでにも登場する場面が多く,球の体積・表面積の公式は小中学校の内に覚えておくとよい.以下の教材では,公式の厳密な証明でもなく,単なる丸暗記でもなく,無理のない範囲で簡単な説明を付けてこれらの公式が使えるようになることを目指す.解説は右→
[球の体積]
半径 r の球の体積を V で表わすと V=πr3 ※ 「身(3)の上に心配(4π)ある( r )さ( 3 )」という覚え方が有名.  ※ 通常,公式丸暗記という学習方法がきらわれるのは,問題が変ったら解けなくなるからであるが,高校数学IIIで実際に微分積分を習うとき以外は球を変形した形(たとえば回転楕円体:右図)などの体積が問われることはない.だから,球の体積については上の公式を覚えるだけでよい. ※ 通常,公式丸暗記という学習方法がきらわれるのは,問題が変ったら解けなくなるからであるが,高校数学IIIで実際に微分積分を習うとき以外は球を変形した形(たとえば回転楕円体:右図)などの体積が問われることはない.だから,球の体積については上の公式を覚えるだけでよい.[例題1] 半径 2 の球の体積を求めなさい. (答案) V=π23=π …(答)  [例題2] 半径 4 の球の上半分の体積を求めなさい. [例題2] 半径 4 の球の上半分の体積を求めなさい.(答案) V=π43×=π …(答)
[問題1]
(1) 半径 3 の球の体積を求めなさい. V=π×33=36π (2) 「直径」 10(cm) の球の体積を求めなさい. 直径が 10(cm) だから半径は 5(cm) V=π×53=π(cm3) (3) 惑星Aの半径が惑星Bの半径の2倍であるとき,惑星Aの体積は惑星Bの体積の何倍か. 惑星Bの半径を r とおくと,その体積は VB=πr3 次に,惑星Aの半径は 2r となるから, その体積は VA=π(2r)3=8× πr3 (「体積比は相似比の3乗比」を使えば,相似比が1:2だから体積比は13:23=1:8 が求まる.) |
解説
○ 円を直径の回りに1回転してできる立体を球という.「球」というときは中身の詰まったもの(球体)を考え,その表面だけを考えるときは「球面」という.  ○ 卓球,テニス,サッカー,バレーボールなど多くの「球技」で使われるボールは,表面のわずかな模様の違いを別とすれば球の形をしている.(ラグビー,アメリカンフットボールのボール,卵などの形は球ではない.)地球は,赤道のあたりが少しふくらんでいるが,ほぼ球の形になっていると考えてよい. ○ ギリシャのアルキメデスの時代から,円柱にすっぽり入る球の体積は,円柱の体積の3分の2になることが知られていた.このことは円柱に水を入れておき,球を沈めてあふれる水の分量を調べると確かめることができる. ○ 右図のように球の外側にぴったり接する円柱を作ると,その底面は半径が r の円,高さは 2r になるから,円柱の体積は V=×2πr3=πr3 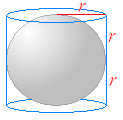 |
|
[球の表面積]
(解説)半径 r の球の表面積を S で表わすと 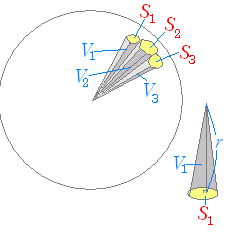 ○ 底面積を S ,高さを h とするとき,三角錐,四角錐,・・・,円錐の体積はいずれも ○ 底面積を S ,高さを h とするとき,三角錐,四角錐,・・・,円錐の体積はいずれも
Sh
になる.これを利用して球の体積を円錐(角錐)の体積で表わすことができる. ○ 右図のように球の中心から球面に向かって「ハチの巣」のような円錐に分ける.このとき,分けられたそれぞれの円錐は右図下に描いたように,球面の一部分が円錐の底面になり,球の半径が円錐の高さに対応する.円錐と円錐を並べると球の表面に隙間ができてしまうように思うかもしれないが,実際には正確な円錐でなくても,三角錐,四角錐,五角錐,・・・,円錐のいずれも体積は(底面積)×(高さ)÷3になるので,球の表面での形にはこだわらなくてもよい.また,右図では円錐の高さというよりは母線の長さが 高さを r になるのではないかと思う人があるかもしれないが,それも正しい.細かく分けると母線の長さと円錐の高さがほとんど等しくなるので,どちらも r としてよい. ○ 各々の円錐(角錐)の体積と底面積の間には,次の関係が成り立つ. V1=S1r V2=S2r V3=S3r … … … 円錐を全部集めると球になり,底面を全部集めると球面になるから V1+V2+V3+…=(S1+S2+S3+ …)r ゆえに,V=Sr …(1) ○ 球の体積は V=πr3 …(2) (1)(2)より πr3=Sr だから,S=4πr2 になる. [例題3] 半径 2 の球の表面積を求めなさい. (答案) S=4π×22=16π …(答) 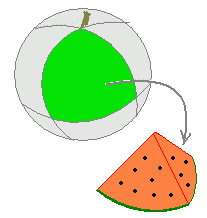 [例題4] 半径 10(cm) のスイカを右図のように縦,横,上下に2等分して8人に分けるとき,1人分のスイカの表面積を求めなさい. [例題4] 半径 10(cm) のスイカを右図のように縦,横,上下に2等分して8人に分けるとき,1人分のスイカの表面積を求めなさい.(答案) 表面の緑色の部分は,球の表面の8分の1だから ×4π×102=50π 切り口の赤色の部分は,円の面積の4分の1が3個あるから ×π×102×3=π 表面積は,50π+π =π=125π(cm2) …(答) |
※ 球の表面積は円の面積の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 V=πr3 を半径で微分すると表面積 S=4πr2 になることが分かる.脱線ついでに言えば,円の面積 S=πr2 を半径で微分すると円周の長さ L=2πr になる. [問題2] (1) 半径 5 の球の表面積を求めなさい. (2) 半径 3 の球の表面積を求めなさい. (3) 球Aの半径が球Bの半径の2倍であるとき,次の空欄を埋めなさい. 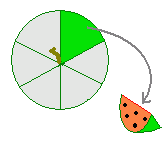 (4) 半径 6(cm) のスイカを右図のように縦に6等分して6人に分けるとき,1人分のスイカの表面積を求めなさい. (4) 半径 6(cm) のスイカを右図のように縦に6等分して6人に分けるとき,1人分のスイカの表面積を求めなさい. |
|
球の体積と表面積(高校入試問題)
【問題1】
解説を見る
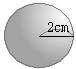 右の図のように,半径が2cmの球があります。この球の表面積を求めなさい。
右の図のように,半径が2cmの球があります。この球の表面積を求めなさい。ただし,円周率は (北海道2018年)
|
【問題2】
解説を見る
半径2cmの球について正しく述べたものを,次のア~エのうちから1つ選び,符号で答えなさい。 ただし,円周率は ア この球の体積は, イ この球の体積は, ウ この球の表面積は, エ この球の表面積は, (千葉県2016年)
|
|
【問題3】
解説を見る
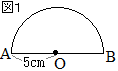 図1の半円を,直線ABを回転の軸として1回転させてできる立体の表面積を求めなさい。ただし,円周率は
図1の半円を,直線ABを回転の軸として1回転させてできる立体の表面積を求めなさい。ただし,円周率は(徳島県2015年)
|
【問題4】
解説を見る
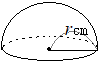 右の図は半径
右の図は半径(鹿児島県2018年)
|
|
■[個別の頁からの質問に対する回答][球の体積と表面積について/17.2.24]
とても役に立ちました(❁ᴗ͈ˬᴗ͈)ペコリ。:.゜ஐ⋆*
■[個別の頁からの質問に対する回答][球の体積と表面積について/17.2.24]
=>[作者]:連絡ありがとう. 問題がついていて、とても良いと思います。
=>[作者]:連絡ありがとう. |
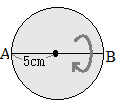 1回転させると,右図のような球になる.
1回転させると,右図のような球になる.