|
※中学校の数学で取り扱える三角形の面積について,このサイトには次の教材があります.
GoogleやYAHOO ! などから検索でこの頁に直接来たが前後関係がよく分からないという場合は,他の頁を先に見てください. が現在地です.
三角形の面積
(中学1年または3年,面積比も登場する)
三角形の等積変形
(中学2年の中点の座標,直線の方程式も使う)
|
|
※中学校の数学で取り扱える三角形の面積について,このサイトには次の教材があります.
GoogleやYAHOO ! などから検索でこの頁に直接来たが前後関係がよく分からないという場合は,他の頁を先に見てください. が現在地です.
三角形の面積
(中学1年または3年,面積比も登場する)
三角形の等積変形
(中学2年の中点の座標,直線の方程式も使う)
|
|
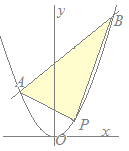
【例題1】 放物線y=x2と直線y=x+2の交点をA, Bとするとき,△AOBの面積を求めてください はじめに,連立方程式  y=x2 …(1)
y=x2 …(1)y=x+2 …(2) を解いて,2交点A, Bの座標を求めます.
(1)を(2)に代入すると
x2=x+2 x2−x−2=0 (x−2)(x+1)=0 x=2, −1 A(−1, 1), B(2, 4) 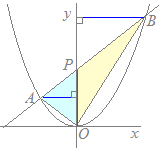 次に,直線y=x+2 …(2)
次に,直線y=x+2 …(2)とy軸との交点(切片)をPとしてPの座標を求めると,P(0, 2) 右図のように△AOBをy軸で2つに分けて,△AOPと△BOPとする. 各々の三角形の底辺をOP=2と考えると高さはA, Bのx座標(の絶対値=符号を正にしたもの)だから, △AOPの高さは1 △BOPの高さは2 三角形の面積は(底辺)×(高さ)÷2で求められるから △AOPの面積は =1 △BOPの面積は =2 よって △AOBの面積は3…(答)
【要点】
三角形をy軸で2つに分けると
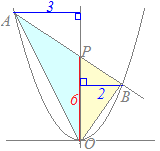 △AOBをABとy軸との交点P(0, 6)を使って,△AOPと△BOPに分ける.
△AOBをABとy軸との交点P(0, 6)を使って,△AOPと△BOPに分ける.OPを底辺と考えると,各々の三角形の底辺の長さはOP=6 高さはA, Bのx座標(の符号を正にしたもの)だから,各々3と2になる. 面積は各々 =9 =6 だから,△APBの面積は15…(答) 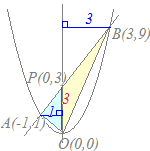 連立方程式
連立方程式 y=x2 …(1)
y=x2 …(1)y=2x+3 …(2) を解いて,2交点A, Bの座標を求める.
(1)を(2)に代入すると
△AOBをABとy軸との交点Pを使って,△AOPと△BOPに分ける.x2=2x+3 x2−2x−3=0 (x−3)(x+1)=0 x=3, −1 A(−1, 1), B(3, 9) OPの長さは直線y=2x+3の切片3に等しい. 高さはA, Bのx座標(の符号を正にしたもの)だから,各々1と3になる. 面積は各々 , だから,△AOBの面積は+=6…(答) |
【例題2】 放物線y=x2と直線y=x+6の交点をA, Bとし,放物線y=x2上の1点をP(1, 1)とするとき,△APBの面積を求めてください 連立方程式  y=x2 …(1)
y=x2 …(1)y=x+6 …(2) を解いて,2交点A, Bの座標を求める.
(1)を(2)に代入すると
x2=x+6 x2−x−6=0 (x−3)(x+2)=0 x=3, −2 A(−2, 4), B(3, 9) 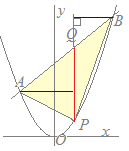 次に,P(1, 1)からy軸に平行な直線をひき,ABとの交点をQとすると
次に,P(1, 1)からy軸に平行な直線をひき,ABとの交点をQとすると x=1 …(3)
x=1 …(3)y=x+6 …(4) より,Q(1, 7) △APBを△APQと△BPQに分けると
PQ=7−1=6
PQを底辺とすると,△APQの高さは
1−(−2)=3
△BPQの高さは
3−1=2
△APQ, △BPQの面積は各々=9,=6 だから,△AOBの面積は9+6=15…(答) 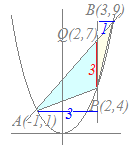 連立方程式
連立方程式 y=x2 …(1)
y=x2 …(1)y=2x+3 …(2) を解いて,2交点A, Bの座標を求める.
(1)を(2)に代入すると
Pを通りy軸に平行な直線x=2と直線y=2x+3との交点をQとすると,Qの座標は次の連立方程式で求められる.x2=2x+3 x2−2x−3=0 (x−3)(x+1)=0 x=3, −1 A(−1, 1), B(3, 9)  x=2 …(3)
x=2 …(3)y=2x+3 …(4) より,Q(2, 7) △APBを△APQと△BPQに分ける. PQの長さは7−4=3に等しい. △APQの高さは2−(−1)=3,△BPQの高さは3−2=1になる. 面積は各々 , だから,△APBの面積は+=6…(答) 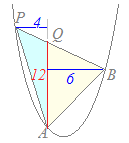 連立方程式
連立方程式 y=x2 …(1)
y=x2 …(1)y=x+4 …(2) を解いて,2交点A, Bの座標を求める.
(1)を(2)に代入すると
x2=x+4 x2=2x+8 x2−2x−8=0 (x−4)(x+2)=0 x=4, −2 A(−2, 2), B(4, 8) 直線PBの方程式を求める.
y=ax+bとおくと
Qの座標は次の連立方程式で求められる.P(−6, 18)を通るから,18=−6a+b…(3) B(4, 8)を通るから,8=4a+b…(4) (3)(4)からa=−1, b=12 y=−x+12  x=−2 …(5)
x=−2 …(5)y=−x+12 …(6) より,Q(−2, 14) △APBを△APQと△ABQに分ける. AQの長さは14−2=12に等しい. △APQの高さは−2−(−6)=4,△ABQの高さは4−(−2)=6になる. 面積は各々 =24,=36 だから,△APBの面積は24+36=60…(答) |
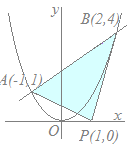
【例題3】 放物線y=x2と直線y=x+2の交点をA, Bとし,x軸上の1点をP(1, 0)とするとき,△APBの面積を求めてください 連立方程式  y=x2 …(1)
y=x2 …(1)y=x+2 …(2) を解いて,2交点A, Bの座標を求める.
(1)を(2)に代入すると
x2=x+2 x2−x−2=0 (x−2)(x+1)=0 x=2, −1 A(−1, 1), B(2, 4) 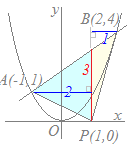 次に,P(1, 0)からy軸に平行な直線をひき,ABとの交点をQとすると
次に,P(1, 0)からy軸に平行な直線をひき,ABとの交点をQとすると x=1 …(3)
x=1 …(3)y=x+2 …(4) より,Q(1, 3) △APBを△APQと△BPQに分けると
PQ=3
PQを底辺とすると,△APQの高さは
1−(−1)=2
△BPQの高さは
2−1=1
△APQ, △BPQの面積は各々, だから,△APBの面積は+=…(答) 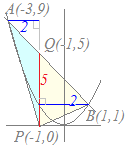 連立方程式
連立方程式 y=x2 …(1)
y=x2 …(1)y=−2x+3 …(2) を解いて,2交点A, Bの座標を求める.
(1)を(2)に代入すると
Pを通りy軸に平行な直線x=−1と直線ABとの交点をQとする.x2=−2x+3 x2+2x−3=0 (x−1)(x+3)=0 x=1, −3 A(−3, 9), B(1, 1) Qの座標は次の連立方程式で求められる.  x=−1 …(5)
x=−1 …(5)y=−2x+3 …(6) より,Q(−1, 5) △APBを△APQと△BPQに分ける. PQの長さは5に等しい. △APQの高さは−1−(−3)=2,△BPQの高さは1−(−1)=2になる. 面積は各々 =5,=5 だから,△APBの面積は5+5=10…(答) 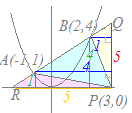 連立方程式
連立方程式 y=x2 …(1)
y=x2 …(1)y=x+2 …(2) を解いて,2交点A, Bの座標を求める.
(1)を(2)に代入すると
Pを通りy軸に平行な直線x=3と直線ABとの交点をQとする.x2=x+2 x2−x−2=0 (x−2)(x+1)=0 x=2, −1 A(−1, 1), B(2, 4) Qの座標は次の連立方程式で求められる.  x=3 …(5)
x=3 …(5)y=x+2 …(6) より,Q(3, 5) △APBを△APQから△BPQを引いたものと考える. PQの長さは5に等しい. △APQの高さは3−(−1)=4,△BPQの高さは3−2=1になる. 面積は各々 , だから,△APBの面積は−=…(答) (別解) 図の桃色で示したように,△APBを△BRPから△ARPを引いたものと考えても簡単にできる. Rのx座標はy=x+2にy=0を代入すれば得られ,R(−2, 0). 底辺をRP=3−(−2)=5(オレンジ色)と考えると △ARPの高さ(緑)は1,△BRPの高さ(緑)は4になる. 面積は各々 , だから,△APBの面積は−=…(答) |
|
|