← PC用は別頁
|
※中学校の数学で取り扱える三角形の面積について,このサイトには次の教材があります.
GoogleやYAHOO ! などから検索でこの頁に直接来たが前後関係がよく分からないという場合は,他の頁を先に見てください. が現在地です.
三角形の面積
(中学1年または3年,面積比も登場する)
三角形の等積変形
(中学2年の中点の座標,直線の方程式も使う)
|
|
※中学校の数学で取り扱える三角形の面積について,このサイトには次の教材があります.
GoogleやYAHOO ! などから検索でこの頁に直接来たが前後関係がよく分からないという場合は,他の頁を先に見てください. が現在地です.
三角形の面積
(中学1年または3年,面積比も登場する)
三角形の等積変形
(中学2年の中点の座標,直線の方程式も使う)
|
|
○三角形の面積は
(面積)=(底辺)×(高さ)÷2
の公式で求められます.次の図のように,△ABCの頂点Aから対辺BCの中点(真ん中の点,1対1に内分する点)Dに線分ADをひくと,△ABDと△DCAとは,底辺が等しく,高さが共通になるから,これら2つの三角形の面積は等しくなります.(高さは底辺と垂直(直角)な線分で測ります) 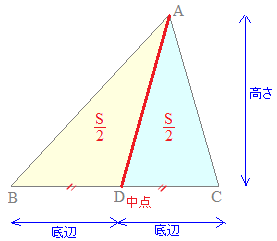 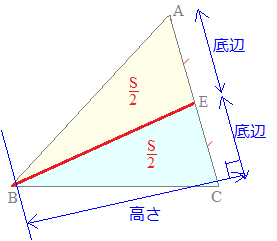
次の図のように,頂点Bから対辺CAの中点Eに線分BEをひいた場合にも,同様にして△BCEと△BAEの面積は等しくなります. 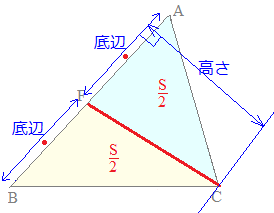
さらに,頂点Cから対辺ABの中点Fに線分CFをひいた場合にも,同様にして△CAFと△CBFの面積は等しくなります.
【要点】
三角形の頂点から対辺の中点にひいた線分は,三角形の面積を二等分する
【例1】
3点A(3, 4), B(1, 2), C(5, 0)を頂点とする△ABCがある. (1) 辺BC上に点Dをとって,線分ADが△ABCの面積を二等分するようにするとき,点Dの座標を求めてください. (2) 辺CA上に点Eをとって,線分BEが△ABCの面積を二等分するようにするとき,点Eの座標を求めてください. (1) 辺AB上に点Fをとって,線分CFが△ABCの面積を二等分するようにするとき,点Fの座標を求めてください.
【ポイント】
(解答)点P(a, b)と点Q(s, t)の中点の座標は ( ※x座標とx座標からx座標を作る,y座標とy座標からy座標を作る. ※1つの座標のx座標とy座標を混ぜてはいけない. (1) B(1, 2), C(5, 0)の中点を点Dとすればよいから 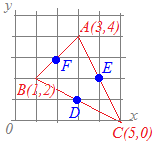 Dのx座標は
Dのx座標はy座標は したがって D(3, 1)…(答)
点の名前とその座標の間には何も入れずにD(3, 1)のように書きます.
(2)D=(3, 1)のようには書かないので注意しましょう. 同様にして だから E(4, 2)…(答) (3) 同様にして だから F(2, 3)…(答)
【例2】
3点A(3, 2), B(0, 0), C(4, 0)を頂点とする△ABCがある. 頂点Aを通り△ABCの面積を二等分する直線の方程式を求めてください.
【ポイント】
(解答)B(0, 0), C(4, 0)の中点D(2, 0)と頂点A(3, 2)を通る直線の方程式を y=ax+b とおいて,この直線がD(2, 0)とA(3, 2)を通るように,a, bの値を求めます. B(0, 0), C(4, 0)の中点をDとおくと,Dの座標は 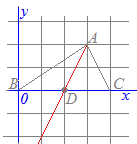 D(2, 0)と頂点A(3, 2)を通る直線の方程式を
D(2, 0)と頂点A(3, 2)を通る直線の方程式をy=ax+b とおくと,この直線がD(2, 0)を通るから 0=2a+b…(1) A(3, 2)を通るから 2=3a+b…(2) (1)(2)の連立方程式を解いてa, bの値を求める. (2)−(1) a=2 これを(1)に代入すると 0=4+b b=−4 ゆえに y=2x−4…(答) |
|
※以下の問題では,正しい選択肢をクリックしてください.解答すれば,解説も読めます.解答しなければ解説は出ません.
A(3, 5), B(1, 1)の中点をDとするとDの座標は
2点D(2, 3), C(5, 0)を通る直線の方程式を 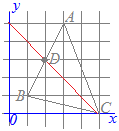 y=ax+b
y=ax+bとおいて,a, bを求める. D(2, 3)を通るから 3=2a+b…(1) C(5, 0)を通るから 0=5a+b…(2) a, bの連立方程式(1)(2)を解く. (2)−(1) −3=3a a=−1 これを(1)に代入 b=5 ゆえに y=−x+5…(答)
【問題2】
3点A(3, 5), B(−2, 3), C(4, −1)を頂点とする△ABCがある. 頂点Aを通り△ABCの面積を二等分する直線の方程式を求めてください. 解説 y=−2x+1 y=−2x−1
B(−2, 3), C(4, −1)の中点をDとするとDの座標は
2点D(1, 1), A(3, 5)を通る直線の方程式を y=ax+b 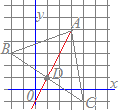 とおいて,a, bを求める.
とおいて,a, bを求める.D(1, 1)を通るから 1=a+b…(1) A(3, 5)を通るから 5=3a+b…(2) a, bの連立方程式(1)(2)を解く. (2)−(1) 4=2a a=2 これを(1)に代入 b=−1 ゆえに y=2x−1…(答)
【問題3】
3点A(−1, 2), B(4, −3), C(3, 4)を頂点とする△ABCがある. 頂点Bを通り△ABCの面積を二等分する直線の方程式を求めてください. 解説 y=−2x+3 y=−2x+5
A(−1, 2), C(3, 4)の中点をDとするとDの座標は
2点D(1, 3), B(4, −3)を通る直線の方程式を y=ax+b とおいて,a, bを求める. 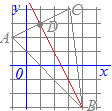 D(1, 3)を通るから
D(1, 3)を通るから3=a+b…(1) B(4, −3)を通るから −3=4a+b…(2) a, bの連立方程式(1)(2)を解く. (2)−(1) −6=3a a=−2 これを(1)に代入 b=5 ゆえに y=−2x+5…(答) |
|
【例3】
3点A(0, 4), B(0, 0), C(3, 0)を頂点とする△ABCがある. 線分BC上の点D(2, 0)を通り△ABCの面積を二等分する直線と線分ABの交点をEとするとき,点Eのy座標を求めてください
【ポイント】
三角形の面積は (面積)=(底辺)×(高さ)÷2 の公式で求められるので, (面積)と(底辺)の長さが決まっていたら,(高さ)が求まる 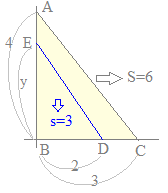 (解答)
(解答)△ABCの面積は △EBDの面積は △ABCの面積を二等分しているのだから
【例4】
3点A(2, 4), B(0, 0), C(6, 0)を頂点とする△ABCがある. 線分BC上の点D(4, 0)を通り△ABCの面積を二等分する直線と線分ABの交点Eの座標を求めてください 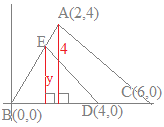 (解答)
(解答)△ABCの面積は Eのy座標をyで表すと △EBDの面積は △ABCの面積を二等分しているのだから ABの直線の方程式は だから, ゆえに
【ポイント】
底辺がx軸上にあれば,高さはy座標
【問題4】
3点A(0, 5), B(0, 0), C(6, 0)を頂点とする△ABCがある. 線分BC上の点D(5, 0)を通り△ABCの面積を二等分する直線と線分ABの交点をEとするとき,点Eのy座標を求めてください 解説 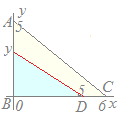 △ABCの面積は
△ABCの面積は△EBDの面積は △ABCの面積を二等分しているのだから
【問題5】
3点A(0, 4), B(0, 0), C(5, 0)を頂点とする△ABCがある. 線分AB上の点D(0, 3)を通り△ABCの面積を二等分する直線と線分BCの交点をEとするとき,点Eのx座標を求めてください. 解説 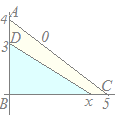 △ABCの面積は
△ABCの面積は△EBDの面積は △ABCの面積を二等分しているのだから
【問題6】
3点A(3, 6), B(0, 0), C(4, 0)を頂点とする△ABCがある. 線分BC上の点D(3, 0)を通り△ABCの面積を二等分する直線と線分ABの交点をEとするとき,点Eの座標を求めてください. 解説 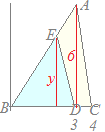 △ABCの面積は
△ABCの面積はEのy座標をyで表すと △EBDの面積は △ABCの面積を二等分しているのだから ABの直線の方程式は だから, ゆえに
【問題7】
3点A(4, 4), B(0, 0), C(5, 0)を頂点とする△ABCがある. 線分BC上の点D(4, 0)を通り△ABCの面積を二等分する直線と線分ABの交点をEとするとき,点Eの座標を求めてください. 解説 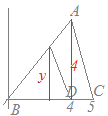 △ABCの面積は
△ABCの面積はEのy座標をyで表すと △EBDの面積は △ABCの面積を二等分しているのだから ABの直線の方程式は だから, ゆえに |
|
【例5】
3点A(0, 3), B(0, 0), C(4, 4)を頂点とする△ABCがある. 線分BC上の点P(3, 3)を通り△ABCの面積を二等分する直線と線分ABの交点をQとするとき,点Qのy座標を求めてください. 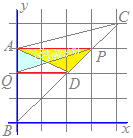 【考え方1】
【考え方1】○BCの中点D(2, 2)と頂点Aを結ぶ線分ADは△ABCの面積を二等分する. ○そうすると,△PABの面積は△ABCの面積の半分よりも△PADの分だけ大きくなっている. ○△PADをPAを底辺として高さを変えずに等積変形すると△PAD=△PAQとなるように点Qを定めることができる. ○そこで,△PABから△PAQを取り除いたもの,すなわち△PQBが△ABCの面積を二等分することになる. BCの中点D(2, 2)と点A(0, 3), P(3, 3)でできる△PADを,PAを底辺として高さを変えない等積変形を行う. Dを通りPAと平行な直線とABとの交点をQとおくと,△PAD=△PAQとなる. PAはx軸に平行だからDQもx軸に平行(y座標を変えない)に取ると Q(0, 2)…(答) 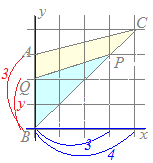 【考え方2】
【考え方2】
この部分は中3の相似図形の性質を習ってからの方がよく分かるが,内容は小学校でも習う
○Q(0, y)とおき,AB, QBを底辺と考えると,底辺の長さの比はAB:QB=3:y○高さの比はC, Pのx座標の比になるから4:3 ○三角形の面積は (面積)=(底辺)×(高さ)÷2 だから,面積の比は (底辺1)×(高さ1):(底辺2)×(高さ2) Q(0, y)とおくと, 底辺の比は3:y 高さの比は4:3 よりy=2 Q(0, 2)…(答)
【例6】
3点A(3, 3), B(−1, −1), C(5, 2)を頂点とする△ABCがある. 線分BC上の点P(3, 1)を通り△ABCの面積を二等分する直線と線分ABの交点をQとするとき,点Qの座標を求めてください 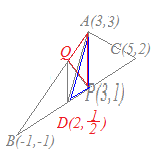 【考え方1】
【考え方1】○BCの中点 ○そうすると,△PABの面積は△ABCの面積の半分よりも△PADの分だけ大きくなっている. ○△PADをPAを底辺として高さを変えずに等積変形すると△PAD=△PAQとなるように点Qを定めることができる. ○そこで,△PABから△PAQを取り除いたもの,すなわち△PQBが△ABCの面積を二等分することになる. BCの中点 Dを通りPAと平行な直線とABとの交点をQとおくと,△PAD=△PAQとなる. PAはy軸に平行だからDQもy軸に平行(x座標を変えない)に取る. Qのx座標はDと同じ2になり,Qは直線AB:y=x上の点だから,Qのy座標は2 Q(2, 2)…(答) 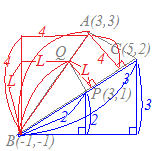 【考え方2】
【考え方2】
この部分は中3の相似図形の性質を習ってからの方がよく分かるが,内容は小学校でも習う
○底辺の比はCB:PB=3:2○高さの比はAB:QB=4:L
長さは各々3,2,4,Lではない.比が3:2, 4:Lだということに注意
○面積の比はとおくと L=3 y座標は2になる. AB:QB=4:Lとおくと, 底辺の比は3:2 高さの比は4:L よりL=3 y座標の差を考えるとAB:QB=3−(−1):y−l(−1)=4:y+1 これが4:3になるのだからy=2 Qは直線AB:y=x上の点だからx=2 Q(2, 2)…(答)
【問題8】
3点A(2, 4), B(0, 0), C(6, 0)を頂点とする△ABCがある. 線分AC上の点P(3, 3)を通り△ABCの面積を二等分する直線と線分BCの交点をQとするとき,点Qの座標を求めてください. 解説 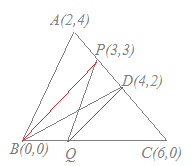 ACの中点D(4,2)と頂点Bを結ぶ線分DBは△ABCの面積を二等分する.
ACの中点D(4,2)と頂点Bを結ぶ線分DBは△ABCの面積を二等分する.△PBCの面積は△ABCの半分よりも△PBDの分だけ多い. △PBDを底辺PBを共通として高さを変えずに等積変形して,頂点Dを移動させて線分BC上にきたとき,その点をQとすると,△PBD=△PBQとなり,△PQCの面積は△ABCの半分になる. P(3,3), B(0,0)を通る直線の傾きは1だから,点D(4,2)を通り,傾き1の直線とBCの交点を求めるとよい. DQの方程式は,傾きが1だから y=x+b とおける.これがD(4,2)を通るから b=−2 y=x−2とBC:y=0との交点を求めると Q(2, 0)…(答) (別解) - - - - - - - - 斜辺の長さをx座標の差で比較すると Qの座標を(x, 0)とおくと より 3(6−x)=12 18−3x=12 3x=6 x=2 ゆえに Q(2, 0)…(答)
【問題9】
3点A(3, 6), B(0, 0), C(8, 4)を頂点とする△ABCがある. 線分BC上の点P(6, 3)を通り△ABCの面積を二等分する直線と線分ABの交点をQとするとき,点Qの座標を求めてください 解説 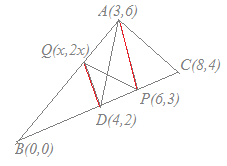 BCの中点D(4,2)と頂点Aを結ぶ線分DAは△ABCの面積を二等分する.
BCの中点D(4,2)と頂点Aを結ぶ線分DAは△ABCの面積を二等分する.△PABの面積は△ABCの半分よりも△PADの分だけ多い. △PADを底辺PAを共通として高さを変えずに等積変形して,頂点Dを移動させて線分AB上にきたとき,その点をQとすると,△PAD=△PAQとなり,△PQBの面積は△ABCの半分になる. P(6,3), A(3,6)を通る直線の傾きは−1だから,点D(4,2)を通り,傾き−1の直線とABの交点を求めるとよい. DQの方程式は,傾きが−1だから y=−x+b とおける.これがD(4,2)を通るから b=6 y=−x+6 次に,ABの方程式はy=2x これらの交点を求めると Q(2, 4)…(答) (別解) - - - - - - - - 斜辺の長さをx座標の差で比較すると Qの座標を(x, 2x)とおくと より x=2 ゆえに Q(2, 4)…(答) |