|
●行列の相等
2つの行列A,Bの型が一致し,かつ,対応する成分が各々等しいとき,AとBは等しいといい,A=Bと書きます。
【例】
【等しくない例】
A=
【等しい例】のとき,型が一致しないからA≠B A=
A=
のとき,A=B |
|
【問題1】
次の空欄を埋めてください.
対応する成分を比較すると,x=3, y=4 になります.
|
|
※高卒から大学初年度向けの「ベクトル,行列」について,このサイトには次の教材があります.
*** ベクトル *** ↓ ●ベクトル.行列の超基本 ●ベクトルの直交条件 ●1次独立,1次従属,基底,次元,核,階数 *** 行列 *** ↓ ●逆行列(1) ●逆行列(2) ↓ ●転置行列,対称行列,対角行列,三角行列 ●行列の階数 *** 行列式 *** ●行列式(1) ●行列式(2) ●行列式(3) *** 一次変換 *** ●行列と一次変換 ●点の像と原像 *** 固有値 *** ↓ ●固有値.固有ベクトルの定義 ↓ ●固有値と固有ベクトル(1) ●固有値と固有ベクトル(2) ●行列の対角化とは ●行列を対角化するには |
|
●行列の相等
2つの行列A,Bの型が一致し,かつ,対応する成分が各々等しいとき,AとBは等しいといい,A=Bと書きます。
【例】
【等しくない例】
A=
【等しい例】のとき,型が一致しないからA≠B A=
A=
のとき,A=B |
|
【問題1】
次の空欄を埋めてください.
対応する成分を比較すると,x=3, y=4 になります.
|
|
●行列の和
2つの行列の型が一致するとき,行列の和を次のように定義します。
2×2行列での例 A+B=
【問題2】
(和が定義できるものをクリック)
次のうち,行列 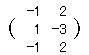 との和が定義できるものを選びなさい。 との和が定義できるものを選びなさい。
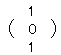 , ,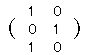 , ,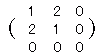 解答
行列
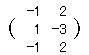 は3×2型(3行2列)なので,これと和が定義できるのは同じ型の行列 は3×2型(3行2列)なので,これと和が定義できるのは同じ型の行列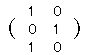 です. です.
【問題3】
●3個以上の行列の和 3個の行列の和は,2つずつの和の繰り返し適用で定義します。
まずA+Bを求めて,その結果にCを足す場合
ただし,行列の和については(A+B)+C …(1) まずB+Cを求めて,その結果をAに足す場合 A+(B+C) …(2) と書きます. 結合法則 (A+B)+C=A+(B+C) が成立するので,(A+B)+Cという意味に理解されても, A+(B+C)という意味に理解されても,同じになります. そこで,単に A+B+C の形に省略して書くことが許されます.・・・(1)のように解釈されても(2)のように解釈されても等しいから 4個の行列の和:((A+B)+C)+D,A+(B+(C+D))についても同様にA+B+C+Dと書くことができます. |
|
●行列の差
2つの行列の型が一致するとき,行列の差を次のように定義します。
2×2行列での例 A-B=
【問題4】
次の計算をしなさい. |
|
●行列の実数倍
行列のt倍は,各成分をt倍した行列とします。
2×2行列での例 |
|
【問題5】
次の計算をしなさい. (1)
(2)
(3)
|
|
●零行列
成分がすべて0である行列を零行列といいます.行列の型が分かっているとき,零行列は単に0で表します。
1×2型の零行列
2×2型の零行列 2×3型の零行列 型が同じとき,A+0=0+A=Aが成立します.
例えば,2×2行列では
が成り立つことは明らかでしょう 任意の行列Aについて0A=0,任意の実数tについてt0=0が成立します.
例えば,2×2行列では
が成り立つことは明らかでしょう
●行列の和の性質
※ 行列で割ることはできませんが,行列の和,差、実数倍,展開などが自由にできるので,次のような行列の方程式も解けます。
また,次のような連立方程式でも { (1)+(2) }÷2や{ (1)−(2) }÷2のような変形は,行列の和,差、実数倍でできるので,普通の連立方程式と同じように解くことができます. ※行列で割ることはできません. 例えば,左辺が2つの行列の積 とすることはできません. 詳しくは,行列の積を学ぶと分かりますが,一般に行列の積は |
|
【問題6】
(1)
(2)
になります |
|
|