.
■相関分析

【要点】
・以下は，よく使われるもの･簡単に求められるもののみ．
・統計データの種類(尺度水準)についてはscale1.htm参照

（※　データが標本である場合には，以下で求めているのは標本の相関係数となるので，母相関係数の推定・検定という問題が別に存在することとなるがこのページでは扱っていない．）
(1)　右の表１のように，データが「量的変数」(数値)と「量的変数」(数値)の組合わせで与えられるとき，相関係数の計算にはピアソンの積率相関係数 r を利用することができる．(※このページ参照)

　相関係数 r は　-1≦ r ≦ 1を満たし，ｒ＞0のとき正の相関，ｒ＜0のとき負の相関，ｒが0付近のとき相関がないと考える．

　ア)　相関係数の定義から求めるときは次の定義による．　
r = 　
(ただし，mはxkの平均，nはykの平均)
　イ)　Excelの分析ツールで簡単に求めることができる．		 表１
生徒番号 国語 社会 数学 理科 英語
No.1 55 70 58 44 50
No.2 53 79 50 41 47
No.3 71 73 44 41 78
No.4 73 75 36 48 70
No.5 67 76 82 88 56
No.6 53 68 33 30 69
No.7 74 76 75 80 82
No.8 50 68 50 44 42
No.9 67 72 48 51 69
No.10 58 78 40 52 61

※　ピアソンの積率相関係数は外れ値（例外的に飛び離れた値）の影響を受けやすく，
　Ｉ）　他のn-1個の標本だけなら相関が見られないときに外れ値を含めただけで「相関らしいものができてしまう場合」や，
　ＩＩ）　逆に，他のn-1個だけならば相関が見られるときに外れ値を含めただけで「相関がなくなる場合」がある
ので，数値計算だけでなく散布図によって外れ値の存在を確認しておくことが重要だと言われている．
(2)　右の表２のように，データが「量的変数」(数値)と「質的変数」(カテゴリーデータ)の組合わせで与えられるときは，相関比を利用することができる．
　平均値の差が有意差と見なせるかどうかは分散分析によって判断できるが，河川と鮎の体長には，次の式で定義される相関比η2(イータ２乗)が利用できる．

　相関比η2 = (群間変動)／(全変動)

※　「一元配置の分散分析」と同じ考え方であるが，分母が全変動となっているので0≦η2≦1となる．		 表２　釣れた鮎の体長（架空データ）
標本 河川 体長
No.01 A川 23.1
No.02 B川 24.7
No.03 A川 24.6
No.04 C川 20.2
No.05 A川 24.5
No.06 C川 18.5
No.07 A川 26.1
No.08 C川 24.0

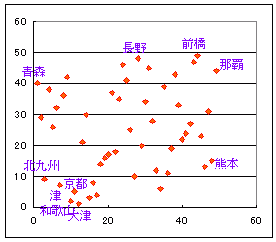
(3)　右の表3のように，デ−タが「順位尺度」の組で与えられているとき，スピアマンの順位相関係数ρを利用することができる．
　ア）
　　(nは対の数)
※　もし同順位のものがあれば，小数を用いて各々を平均順位とする．
（例）　1位，2位，2位，4位，5位，･･･
　　===>　２位の２つは，2位，3位を分けたものだから，各々2.5位とし，　1，2.5，2.5，4，5，･･･　とする．

　イ）　スピアマンの順位相関係数は，順位を単なる数値と見なして「ピアソンの積率相関係数」に当てはめたものに等しいので，Excelの分析ツールで単に相関を出力したものと同じになる．

※　スピアマンの順位相関係数は，「順序尺度」のデータに四則演算を行うため，理論的な弱点が指摘されることがある．		 表３　県庁所在都市における１世帯当り消費量(g)の多い順
県庁所在地 魚介類 肉類
青森市 1 40
富山市 2 29
北九州市 3 9
秋田市 4 38
金沢市 5 26
鳥取市 6 32
津市 7 7
仙台市 8 36
盛岡市 9 42
和歌山市 10 2
京都市 11 5
大津市 12 1
東京区部 13 21
･･･ ･･･ ･･･
※　データの出所：総務省統計局／平成16〜18年　平均の家計調査品目別データ（都道府県庁所在市別ランキング）
(4)　右の表４ように，データが「質的変数」（カテゴリーデータ）と「質的変数」のクロス集計表（分割表）で与えられるとき，
　または，右の表５のように「量的変数」の組が階級分けしてクロス集計のみ与えられ，元データが不明のとき（元データがあるときはピアソンの相関係数でやればよい），
　クラメールの連関係数(クラメールのＶ，独立係数)を利用することができる．
　これは，χ2分布を用いた「独立性の検定」を少し変形したものとなっている．

　※　クロス集計表（分割表）の作り方はこのページ


　右の表O，表Eを用いて３行４列で解説する．
　χ2値は右の表Ｏのような観測値に対して，その周辺和から比例配分した期待度数を表Eのように作成し，
χ2 =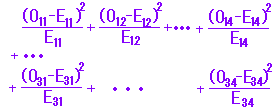
を計算したものであるが，この値は　0≦χ2＜∞　の値をとる．（項目1〜4と項目A〜Cが独立のとき，χ2値は0となる．）
　この値χ2を要素の個数によらず0〜1の値をとるように調整した次の値をクラメールの連関係数（独立係数）という．
　　(0≦C≦1)
（Ｎは度数の総和，ｋはカテゴリｰ数の小さい方：右の例では3．　なお，この連関係数は，質的変数と質的変数の関係なので「負の相関」ということは考えない．）		 表４
性別／態度 支持する 支持しない どちらとも
言えない		 総計
男 19 14 14 47
女 16 25 12 53
総計 35 39 26 100
表５
項目１／項目2 5-10 10-15 15-20 20-25 総計
5-10 0 2 12 15 29
10-15 0 2 16 12 30
15-20 10 10 1 1 22
20-25 10 7 2 0 19
総計 20 21 31 28 100
表O
観測度数　 項目1 項目2 項目3 項目4 計
項目A O11 O12 O13 O14 n1･
項目B O21 O22 O23 O24 n2･
項目C O31 O32 O33 O34 n3･
計 n･1 n･2 n･3 n･4 n
表E
期待度数　 項目1 項目2 項目3 項目4 計
項目A E11 E12 E13 E14 n1･
項目B E21 E22 E23 E24 n2･
項目C E31 E32 E33 E34 n3･
計 n･1 n･2 n･3 n･4 n

■Excelにおける操作■
(1)　　ア)
　　ピアソンの積率相関係数を定義に従って求める方法：（ただし，この方法では２つずつ求めるので，列数が多いと組合わせの数だけ求めることとなり，作業量は多くなる．）

右の表６のように，x1，x2が与えられたとき，これらの平均を各々m，nとすると，
i)　B12に=AVERAGE(B2:B11)，これを12にコピー･貼り付け
 m= 51.6，n=51.9となる．
ii)　Ｄ列に(x1の偏差)=(x1の各値)-(x1の平均)の式を書く．
　D2には =B2-B$12
　これをC11までコピー・貼り付け，E列も同様
iii)　Ｆ列のこれらの積を書き込む
　F2は =D2*E2
iv)　X1の分散を求める：　D13に =SUMSQ(D2:D11)
　　　x2の分散も求める：　E13に=SUMSQ(E2:E11)
　　（※SUMSQ()は２乗の和を求める関数）
v)　x1，x2の共分散を求める：F13に　=SUM(F2:F11)
vi)　x1，x2の相関係数を求める：
　D14に　=F13/SQRT(D13*E13)		 表６
　 A B C D E F
1 生徒番号 x1 x2 (x1-m) (x2-n) (x1-m)(x2-n)
2 No.1 58 44 6.400 -7.900 -50.560
3 No.2 50 41 -1.600 -10.900 17.440
4 No.3 44 41 -7.600 -10.900 82.840
5 No.4 36 48 -15.600 -3.900 60.840
6 No.5 82 88 30.400 36.100 1097.440
7 No.6 33 30 -18.600 -21.900 407.340
8 No.7 75 80 23.400 28.100 657.540
9 No.8 50 44 -1.600 -7.900 12.640
10 No.9 48 51 -3.600 -0.900 3.240
11 No.10 40 52 -11.600 0.100 -1.160
12 平均 51.6 51.9 　 　 　
13 　 　 　 2312.400 2950.900 2287.600
14 　 　 　 0.876 　 　
(1)　　イ)
　　ピアソンの積率相関係数をExcelの分析ツールを利用して求める方法：
　右の表７において，国語〜英語までの５教科の相関係数を一度に求めるには：
i)　メニュー→ツール→分析ツール→相関→ＯＫ
ii)　入力元　入力範囲　
　　先頭行のラベルも含めてB1：F11を範囲とする．
　　データ方向　列
　　ラベル　チェック　→　ＯＫ

iii)　右の表８のように出力される．（小数点以下の桁数はもっと多い．）

　例えば，数学と理科の得点の相関係数は0.876と読む．
　（自分自身との相関係数は1となっている．）

　※　相関係数行列が必要なときは，「コピーして，編集→（どこか作業範囲に）形式を選択して貼り付け→行と列を入れ替える
　さらに，対角成分のみ取り除いてから
編集→形式を選択して貼り付け→値，加算」　とすればできる．		 表７
　 A B C D E F
1 生徒番号 国語 社会 数学 理科 英語
2 No.1 55 70 58 44 50
3 No.2 53 79 50 41 47
4 No.3 71 73 44 41 78
5 No.4 73 75 36 48 70
6 No.5 67 76 82 88 56
7 No.6 53 68 33 30 69
8 No.7 74 76 75 80 82
9 No.8 50 68 50 44 42
10 No.9 67 72 48 51 69
11 No.10 58 78 40 52 61
表８
　 国語 社会 数学 理科 英語
国語 1.000 　 　 　 　
社会 0.364 1.000 　 　 　
数学 0.283 0.260 1.000 　 　
理科 0.543 0.456 0.876 1.000 　
英語 0.786 0.115 -0.065 0.181 1.000


(2)
　右の表９のように質的変数（カテゴリーデータ）と量的変数（数値）の組で与えられる変数間の相関比を求めるには：

ア)　定義に従って計算するとき
　まず，質的変数をキーにしてソートし（表10），各カテゴリーごとに列に並べると表11のようになる．

i)　(群内変動)=Σ(各値-各群の平均値)2を求める．
　群内平均
　　A14に=AVERAGE(A2:A12)
　　これをコピーし，B14：C14に貼り付け
　全体平均
　　A16に=AVERAGE(A2:C12)
　偏差
　　E2に　=A2-A$14
　　これをコピーし，G12まで貼り付け
　群内変動
　　A群：E13に　=SUMSQ(E2:E12)
　　これをコピーし，G13まで貼り付け
　　H13に　=SUM(E13:G13) =55.1となる．

ii)　（群間変動）=Σ(群平均-全体平均)2　（ただし，各々の群の標本数を掛けるのを忘れないことが重要）
　　E14に　=COUNT(A2:A12)*(A14-$A$16)^2
　　これをコピーし，G14まで貼り付け
　　H14に=SUM(E14:G14) = 47.5となる．

iii)　（全変動）=(群内変動)+(群間変動)
　　H15に　=SUM(H13:H14) = 102.6となる．
　　（※　Σ（各値-全体平均）2と等しくなる）

jv)　（相関比）＝（群間平均）／（全体平均）
　　H16に =P14/P15 =0.463となる．

イ)　分析ツールを利用するとき
メニュー→ツール→分析ツール→分散分析：一元配置
で，表11の表を（表10ではない）入力範囲として指定すると，表12のように出力されるが，この表から
（相関比）=（群間平均）／（全体平均）
を計算すればよい．		 表９　釣れた鮎の体長と河川の関係
標本 河川 体長
No.01 A川 23.1
No.02 B川 24.7
No.03 A川 24.6
No.04 C川 20.2
No.05 A川 24.5
･･･ ･･･ ･･･
表10
標本 河川 体長
No.01 A川 23.1
No.03 A川 24.6
No.05 A川 24.5
･･･ ･･･ ･･･
No.12 B川 22.3
No.14 B川 21.0
No.15 B川 21.2
・・・ ･･･ ･･･
No.18 C川 22.4
No.20 C川 22.5
No.21 C川 22.6
･･･ ･･･ ･･･
表11
　 A B C D E F G H
1 A川 B川 C川 　 A偏差 B偏差 C偏差 　
2 23.1 24.7 20.2 　 -1.3 2.9 -1.3 　
3 24.6 20.8 18.5 　 0.2 -1.0 -3.0 　
4 24.5 22.3 24.0 　 0.1 0.5 2.5 　
5 26.1 21.0 20.5 　 1.7 -0.8 -1.0 　
6 22.5 21.2 22.4 　 -1.9 -0.6 0.9 　
7 22.6 20.8 22.5 　 -1.8 -1.0 1.0 　
8 24.5 　 22.6 　 0.1 　 1.1 　
9 26.7 　 21.0 　 2.3 　 -0.5 　
10 25.5 　 　 　 1.1 　 　 　
11 22.6 　 　 　 -1.8 　 　 　
12 25.4 　 　 　 1.0 　 　 和
13 平均 　 　 群内
変動		 22.2 11.7 21.2 55.1
14 24.4 21.8 21.5 群間
変動		 26.4 6.3 14.8 47.5
15 全体 　 　 　 　 　 全変動 102.6
16 22.8 　 　 　 　 　 相関比 0.463
表12
分散分析表 　 　 　 　 　 　
変動要因 変動 自由度 分散 観測された分散比 P-値 F　境界値
グループ間 47.51 2 23.75 9.49 0.00 3.44
グループ内 55.08 22 2.50 　 　 　
　 　 　 　 　 　 　
合計 102.59 24 　 　 　 　


(3)
　右の表13のような順位表から２つの順位の相関を調べたいとき．（右の例は，魚介類の消費量と肉類の消費量の相関を調べようとしたもの：魚をよく食べる都市は肉は少ないのではないかとの仮説を立てて検証してみる．）

　ア）　スピアマンの順位相関係数ρを次の定義式で計算する方法
　　(nは対の数)

i)　順位の差を求める．D2に =B2-C2
　　この式をコピーしてD50まで貼り付け．
ii)　Σ(順位差)2 を求める．
　D51に =SUMSQ(D2:D50)
iii)　ρの定義式に当てはめる：
　D52に =1-6*D51/(49^3-49)
※　相関係数は0.20となり，相関はほとんど見られないが，魚が多いと肉が少ないのでなく，弱い正の相関となる･･･肉も魚もよく食べる都市，肉も魚もあまり食べない都市がある．（右の散布図参照･･･順位相関を散布図にするとき，左と下が数値が小=順位が上位になるので注意）
イ）　分析ツールを用いる方法は，(1)　イ）と同様（順位を数値として扱う．）
 表13　県庁所在都市における１世帯当り消費量(g) の多い順
　 A B C D
1 県庁所在地 魚介類 肉類 差
2 青森市 1 40 -39
3 富山市 2 29 -27
4 北九州市 3 9 -6
5 秋田市 4 38 -34
6 金沢市 5 26 -21
7 鳥取市 6 32 -26
･･･ ･･･ ･･･ ･･･ ･･･
50 那覇市 49 44 5
51 　 　 平方和 15612
52 　 　 相関係数 0.20
※　データの出所：総務省統計局／平成16〜18年　平均の家計調査品目別データ（都道府県庁所在市別ランキング）


.
(4)
　右の表14のように質問項目Q1とQ2に対する回答についてクラメールの連関係数（独立係数）を求めるには：
i)　表15　のように周辺和を元にしてア〜エとA〜Dが独立（無相関）と仮定した場合の期待度数を計算する．
 B9に　=B$13*$F9/$F$13
　この式をコピーし，E12まで貼り付け．
ii)　表16　のように各セルについて (観測度数 - 期待度数)2/(期待度数)　を計算する：
　B16に　=(B2-B9)^2/B9
　この式をコピーし，E19まで貼り付け．
iii)　χ2値を求める： F20に　=SUM(B16:E19)
iv)　クラメールの連関係数(独立係数)を求める：
　総度数は N= 50，行数と列数の内小さい方は(どちらでも)4だから
　=SQRT(F20/(50*3))　により 0.399 となる．		 表14
　 A B C D E F
1 Q1/Q2 ア イ ウ エ 　
2 A 1 2 3 1 7
3 B 2 7 6 0 15
4 C 2 1 5 3 11
5 D 7 0 2 8 17
6 　 12 10 16 12 50
表15
　 A B C D E F
8 Q1/Q2 ア イ ウ エ
9 A 1.68 1.4 2.24 1.68 7
10 B 3.6 3 4.8 3.6 15
11 C 2.64 2.2 3.52 2.64 11
12 D 4.08 3.4 5.44 4.08 17
13 　 12 10 16 12 50
表16
　 A B C D E
15 Q1/Q2 ア イ ウ エ
16 A 0.28 0.26 0.26 0.28
17 B 0.71 5.33 0.30 3.60
18 C 0.16 0.65 0.62 0.05
19 D 2.09 3.40 2.18 3.77

確率統計のメニューに戻る 高校数学のメニューに戻る
■［個別の頁からの質問に対する回答］[相関分析について／16.12.20］
大変わかりやすい説明でした。 最後のクラメールの計算についてわからない点があります。手元の教科書ではクロス表の縦計、横計に1つでも「0」がある場合、独立係数は計算できません、とあります。これはそれぞれ表14で言うと「ア」や「A」と答えた人の合計値を差し示し、「B2:E5」の黄色の範囲にある個別の回答者数は「0」であっても構わないということでしょうか？また2×2のクロス集計ではよくイエーツの補正が紹介されていますが、それ以上のクロス表については記載が見つかりません。このような場合補正方法はないのでしょうか？それともマス数が多く数値が十分あるため、補正しなくとも相関性について十分な吟味をすることができる、という考えがなされているのでしょうか？このような細かい疑問点についても書かれていると個人的に大変うれしいです。
＝＞［作者］：連絡ありがとう．縦または横の合計が０の場合，期待度数の計算で分母が０になるのでできないと思います．しかし個別の度数が０であることは問題ありません．
カイ２乗検定で２×２のクロス表の場合だけはカテゴリーの併合を行ってしまうと表がなくなってしまうのに対して，マス数が大きな表ではどのマスの期待度数も４より大きくなるようにカテゴリーの併合を行うことができるので問題がないと考えます．