|
■ 解説 「速さ」「時間」「距離(道のり)」の間には次の関係があります。 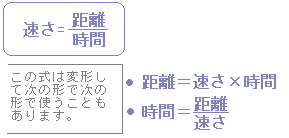 例  |
| ※高度な考察： 単位は，計算の足跡を残しています。 例えば，速さの単位がm/秒であるとき，その量は距離(m)を時間(秒)で割ったものであることを表わしています。 |
|
■ 解説 「速さ」「時間」「距離(道のり)」の間には次の関係があります。 例 |
| ※高度な考察： 単位は，計算の足跡を残しています。 例えば，速さの単位がm/秒であるとき，その量は距離(m)を時間(秒)で割ったものであることを表わしています。 |
|
■問題 次の各問について，正しいものを選びなさい。
問題1 時速 5 (km) の速さで x (時間)歩いたときに進む距離 (km)
|
（距離）=（速さ）×（時間）だから，5×x=5x
|
|
問題2 5 (km) の道を x (時間)で歩いたときの平均の速さ(km/時) |
|
（速さ）=（距離）÷（時間）だから，5÷x=
|
|
問題3 x (km) の道を時速 5 (km) で歩くのに要する時間(時間) |
|
（時間）=（距離）÷（速さ）だから，x÷5=
|
|
問題4 50 (km) の道を時速 15 (km) の自転車で x (時間)行ってから残りを歩くとき，歩く距離 (km)
|
|
（距離）=（速さ）×（時間）だから，自転車で行った距離は15×x=15x
残りの距離は50−15x |
問題5 ある道を往復するのに行きは時速 x (km) の自転車を使い，帰りは時速 5 (km) で歩くものとする。行きに自転車で 2 (時間)かかったとき，帰りに要する時間(時間)
|
|
（距離）=（速さ）×（時間）だから，行きの距離は2×x=2x
これと等しい帰りの距離を時速 5 (km) で歩くに要する時間を，（時間）=（距離）÷（速さ）で求めると 2x÷5= |
問題6 秒速 a (m) の列車が b (秒)走ったとき進む距離(m)
|
|
（距離）=（速さ）×（時間）だから，a×b=ab
|
問題7 a (m) の道のりを秒速 b (m) で進むのに要する時間(秒)
|
|
（時間）=（距離）÷（速さ）だから，a÷b=
|
問題8 a (m) の道のりを b (秒)で進んだときの速さ(m/秒)
|
|
（速さ）=（距離）÷（時間）だから，a÷b=
|
問題9 時速 a (km) で 2 (時間)歩き，さらに時速 b (km) の自転車で 3 (時間)走ったときの全体の道のり(km)
|
|
（距離）=（速さ）×（時間）だから，歩いた距離は2a，自転車で走った距離は3b
全体の距離は2a+3b |
問題10 50 (km) の道のりを時速 a (km) の自転車で b (時間)進んだとき，残りの道のり(km)
|
|
（距離）=（速さ）×（時間）だから，自転車で進んだ距離はab(km)
残りの距離は50−ab(km) |
 ...（携帯版）メニューに戻る...（PC版）メニューに戻る |