|
○1 y=acosxのaの値は,「中腹から山頂までの山の高さ」を表しています.(縦方向に引き延ばす倍率になります.) 次の図はy=2cosxのグラフを表しています. y=−1cosxのようにaが負の値のときは,上下が逆になります. y=−2cosxのときは,上下が逆で2倍に引き延ばしたものになります。  ○2 y=cosbxのbの値は,横方向に縮める倍率を表しています. 次の図はy=cos2xのグラフを表しています. 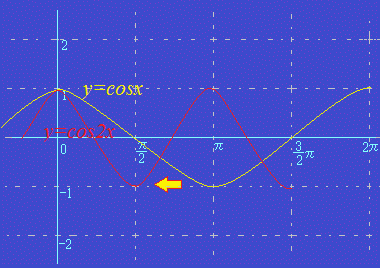
y=cos2xのときに,横方向がになり,
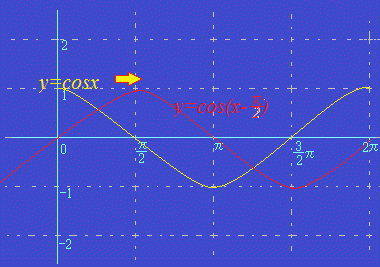
y=cosのときに,横方向に2倍になります. ※この部分は,間違いやすいので注意してください. ※0≦x≦πの間だけで,0≦2x≦2πになるので,cos2xはcos0からcos2πまで一周すると考えるとよいでしょう.  |