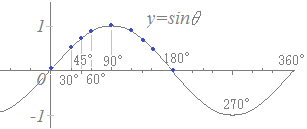
|
【例題1】
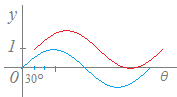
y=sin(2θ+90°)のグラフはy=sin2θのグラフをどのように平行移動したものか.
(解答)
y=sin2(θ+45°)と変形する.
θ軸の正の向きに−45°だけ平行移動したもの…(答)
(左に45°平行移動したもの)
※+90°となっているからと言って90°と答えてはいけない.
※変形して+45°となるからと言って+45°と答えてはいけない.
【例題2】
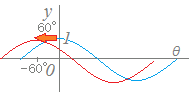
y=cos(3θ−90°)のグラフはy=cos3θのグラフをどのように平行移動したものか.
(解答)
y=cos3(θ−30°)と変形する.
θ軸の正の向きに30°だけ平行移動したもの…(答)
(右に30°平行移動したもの)
※−90°となっているからと言って−90°と答えてはいけない.
※変形して−30°となるからと言って−30°と答えてはいけない.
【例題3】
y=tan(3θ+60°)−2のグラフはy=tan3θのグラフをどのように平行移動したものか.
(解答)
y=cos3(θ+20°)−2と変形する.
θ軸の正の向きに−20°,y軸の正の向きに−2平行移動したもの…(答)
(左に20°,下に2だけ平行移動したもの)
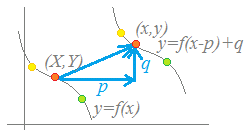
※y軸方向の移動量はy=f(x−p)+qのqをそのまま読めばよい.
yは何もズルくない!!
→ y−q=f(x−p)の形で考えると
θ軸方向にp,y軸方向にqになりお互い様なのだ
次の各問題に答えてください.(解答は下の選択肢から正しいものをクリック)
【問題1】
y=sin(2θ+120°)のグラフはy=sin2θのグラフをどのように平行移動したものか.
y=sin2(θ+60°)と変形する.
θ軸の正の向きに−60°だけ平行移動したもの…(答)
【問題2】
y=sin(3θ−120°)のグラフはy=sin3θのグラフをどのように平行移動したものか.
y=sin3(θ−40°)と変形する.
θ軸の正の向きに40°だけ平行移動したもの…(答)
【問題3】
&chf=bg,s,ffffdd) \( y=\cos (\dfrac{1}{2}\theta +60^{\circ}) \) \( y=\cos (\dfrac{1}{2}\theta +60^{\circ}) \)のグラフは  \( y=\cos \dfrac{1}{2}\theta \) \( y=\cos \dfrac{1}{2}\theta \)のグラフをどのように平行移動したものか.
&chco=aa4422) \( y=\cos \dfrac{1}{2}(\theta + 120^{\circ}) \) \( y=\cos \dfrac{1}{2}(\theta + 120^{\circ}) \)と変形する.
θ軸の正の向きに −120°だけ平行移動したもの…(答)
※2でくくるときは係数を2で割る.同様にして  \( \frac{1}{2} \) \( \frac{1}{2} \)でくくるときは係数を  \( \frac{1}{2} \) \( \frac{1}{2} \)で割る.すなわち2を掛ける.(展開したときに元の60°に戻ればよい)
【問題4】
&chf=bg,s,ffffdd) \( y=\cos (\dfrac{1}{3}\theta -60^{\circ}) \) \( y=\cos (\dfrac{1}{3}\theta -60^{\circ}) \)のグラフは  \( y=\cos \dfrac{1}{3}\theta \) \( y=\cos \dfrac{1}{3}\theta \)のグラフをどのように平行移動したものか.
&chco=aa4422) \( y=\cos \dfrac{1}{3}(\theta-180^{\circ}) \) \( y=\cos \dfrac{1}{3}(\theta-180^{\circ}) \)と変形する.
θ軸の正の向きに 180°だけ平行移動したもの…(答)
※3でくくるときは係数を3で割る.同様にして  \( \dfrac{1}{3} \) \( \dfrac{1}{3} \)でくくるときは係数を  \( \dfrac{1}{3} \) \( \dfrac{1}{3} \)で割る.すなわち3を掛ける.(展開したときに元の−60°に戻ればよい)
【問題5】
y=sin(3θ−90°)−1のグラフはy=sin3θのグラフをどのように平行移動したものか.
y=sin3(θ−30°)−1と変形する.
θ軸方向に30°,y軸方向に−1だけ平行移動したもの…(答)
|
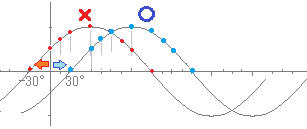
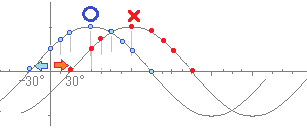
 【例1】
【例1】