|
10進法で書かれた小数
10進法で書かれた小数12.345は1×10+2+3×+4×+5× を表します.
a,b,c,d,eが0,1,2,3,...,8,9の数字であるとき,10進法で書かれた小数abc.deは
a×102+b×10+c+d×+e× を表します. ※ 小数第n位の数は,の係数になっています.
2進法で書かれた小数
a,b,c,d,eが0,1の数字であるとき,2進法で書かれた小数abc.de(2)は
a×22+b×2+c+d×+e× を表します. ※ 小数第n位の数は,の係数になっています.
○ 10進法で書かれた小数を2進法で表すには,次のように考えると簡単です.
(1) 2進法で書かれた数は,2倍すると左に1桁ずつシフトします.(1桁ずつずれるだけ・・・2進法で2倍するのはものすごく簡単!) a×22+b×2+c+d×+e× 2倍する a×23+b×22+c×2+d+e× 2倍する a×24+b×23+c×22+d×2+e 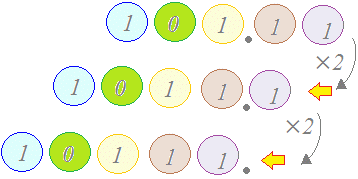
(2) そこで,10進法で書かれた数を2進法で表すには,まず,整数部分と小数部分に分けます.
1) 整数部分は,今まで通りに2進法で表します. 2) 小数部分だけを[1]「2倍して」,[2]「頭を読み取り」,[3]「頭を取り除きます」 (これを繰り返します) 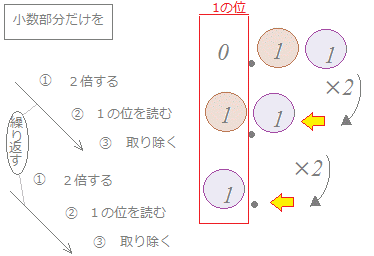 |
|
【例1】
(解説)2進法で表された小数10.11(2)を10進法の分数で表してください. 10.11(2)=1×2+0+1×+1× =2++=
【例2】
(解説)2進法で表された小数11.1(2)を10進法の小数で表してください. 11.1(2)=1×2+1+1× =2+1+==3.5
【例3】
(解説)10進法で表された小数5.75を2進法の小数で表してください. (整数部分) 5=1×22+0×2+1=101(2) (小数部分)
[1]2倍すると
(全体で)101.11(2) …(答)0.75×2=1.5 ←[2]頭の数字は1 [3]1を取り除くと 0.5 [1]2倍すると 0.5×2=1 ←[2]頭の数字は1 小数部分は0.11(2)
【例4】
(解説)10進法で表された小数13.625を2進法の小数で表してください. (整数部分) 13=1×23+1×22+0×2+1=1101(2) (小数部分)
[1]2倍すると
(全体で)1101.101(2) …(答)0.625×2=1.25 ←[2]頭の数字は1 [3]1を取り除くと 0.25 [1]2倍すると 0.25×2=0.5 ←[2]頭の数字は0 [3]0だから取り除く必要はない 0.5 [1]2倍すると 0.5×2=1 ←[2]頭の数字は1 [もうないので終り] 小数部分は0.101(2) |
|
11.101(2)=1×2+1+1×+0×+1×
=2+1++= →4
1011.011(2)=1×23+0×22+1×2+1+0×+1×+1×
=8+0+2+1++==11.375 →1
|
|
(整数部分)
6=1×22+1×2+0=110(2) (小数部分)
[1]2倍すると
(全体で)110.0101(2) …(答)0.3125×2=0.625 ←[2]頭の数字は0 [3] 0だから取り除いても取り除かなくても同じ 0.625 [1]2倍すると 0.625×2=1.25 ←[2]頭の数字は1 [3] 1を取り除くと 0.25 [1]2倍すると 0.25×2=0.5 ←[2]頭の数字は0 [3] 0だから取り除いても取り除かなくても同じ 0.5 [1]2倍すると 0.5×2=1 ←[2]頭の数字は1 [もうないので終り] 小数部分は0.0101(2) →2
|
|
【参考:Excelを使った検算】
○Excelには2進数の「正の整数」を10進数の正の整数に変換する関数 =BIN2DEC() がありますが,この関数のままでは2進数の「小数」を10進数の小数に変換することはできません. そこで,11.101を10進数に直すには,下図の流れに沿って
(1) 初めに8倍して「正の整数」に直す.(2進数を3桁繰り上げるには8倍するとよい)
という手順で,2進数の「小数」を10進数の小数に変換できます.→【問題2】の答の検算ができます(2) 次に,これを10進数に変換する. (3) 得られた10進数を8で割る. 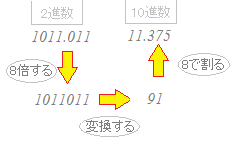 ※ただし,この関数 =BIN2DEC(**) は,引数(**)の値の範囲が≦11111111(2)=511となっているようです.引数がこれよりも大きいと負の数が返されます. |
|
○Excelには10進数の「正の整数」を2進数の正の整数に変換する関数 =DEC2BIN() があります.【例3】のように10進数の「小数」を2進数の小数に変換するには,左欄の逆の手順のように見えますが,割り算を簡単に行うには2,4,8,..倍して2,4,8,..で割るのがよいようです.
(1) 初めに2n倍して「正の整数」に直す.(2,4,8,..とやってみて整数になればよい)
という手順で,10進数の「小数」を2進数の小数に変換できます.(2) 次に,これを2進数に変換する. (3) 得られた2進数を2nで割る. ※ただし,この関数 =DEC2BIN(**) は,引数(**)の値の範囲が**≦511=11111111(2)となっているようですので,引数の範囲を超えてしまうときは無理です. ※また,2n倍で整数にならないときは無理です. 【例3】の場合
(1) 5.75×4=23で整数になる.
【例4】の場合(2) DEC2BIN(23)=10111 により,2進数になる. (3) 4で割るから,2桁下げて101.11が答
(1) 13.625×8=109で整数になる.
【問題3】の場合(2) DEC2BIN(109)=1101101 により,2進数になる. (3) 8で割るから,3桁下げて1101.101が答
(1) 6.3125×16=101で整数になる.
(2) DEC2BIN(101)=1100101 により,2進数になる. (3) 16で割るから,4桁下げて110.0101が答 |
|
3進法で書かれた小数
a,b,c,d,eが0,1,2の数字であるとき,3進法で書かれた小数abc.de(3)は
a×32+b×3+c+d×+e× を表します. ※ 小数第n位の数は,の係数になっています.
○ 10進法で書かれた小数を3進法で表すには,次のように考えると簡単です.
(1) 3進法で書かれた数は,3倍すると左に1桁ずつシフトします. a×32+b×3+c+d×+e× 3倍する a×33+b×32+c×3+d+e× 3倍する a×34+b×33+c×32+d×3+e (2) そこで,10進法で書かれた数を3進法で表すには,まず,整数部分と小数部分に分けます. 1) 整数部分は,今まで通りに3進法で表します. 2) 小数部分だけを[1]「3倍して」,[2]「頭を読み取り」,[3]「頭を取り除きます」 (これを繰り返します) ⇒ 右の【例7】
21.22(3)=2×3+1+2×+2×
=6+1++= →4
1.21(3)=1+2×+1×
=1++= =1.7···(循環小数) →4
|
|
【例5】
(解説)3進法で表された小数2.01(3)を10進法の分数で表してください. 2.01(3)=2+0×+1× =2+=
【例6】
(解説)3進法で表された小数10.12(3)を10進法の小数で表してください. 10.12(3)=1×3+0+1×+2× =3++= =3.555···(循環小数)
【例7】
(解説)10進法で表された小数5.7を3進法の小数で表してください. (整数部分) 5=1×3+2=12(3) (小数部分)
[1] 3倍すると
=== 初めの問題に戻っているので≪繰り返しになる≫ ===0.7×3=2.1 ←[2]頭の数字は2 [3] 2を取り除くと 0.1 [1] 3倍すると 0.1×3=0.3 ←[2]頭の数字は0 [3] 0だから取り除いても取り除かなくても同じ 0.3 [1] 3倍すると 0.3×3=0.9 ←[2]頭の数字は0 [3] 0だから取り除いても取り除かなくても同じ 0.9 [1] 3倍すると 0.9×3=2.7 ←[2]頭の数字は2 [3] 2を取り除くと 0.7 小数部分は0.2002 2002 ···(3)(循環小数) (全体で)12.2002 2002 2002 ···(3)(循環小数)
【問題6】
10進法で表された小数3.5を3進法の小数で表してください. 12.1···(3)(循環小数) 23.2···(3)(循環小数) 310.1···(3)(循環小数) 410.3···(3)(循環小数) 解説
(整数部分)
※3, 6, 7, 9 など2, 5以外の因数を持つnを底とするn進数では,10進数と有限小数⇔循環小数が入れ替わることがあります.
3=1×3+0=10(3) (小数部分)
[1] 3倍すると
全体で10.1···(3)0.5×3=1.5 ←[2]頭の数字は1 [3] 1を取り除くと 0.5 ≪繰り返しになるから≫ 小数部分は0.111···(3)(循環小数) →3
|
|
8進法で書かれた小数
a,b,c,d,eが0,1,2,...,6,7の数字であるとき,8進法で書かれた小数abc.de(8)は
a×82+b×8+c+d×+e× を表します. ※ 小数第n位の数は,の係数になっています.
○ 10進法で書かれた小数を8進法で表すには,次のように考えると簡単です.
(1) 8進法で書かれた数は,8倍すると左に1桁ずつシフトします. a×82+b×8+c+d×+e× 8倍する a×83+b×82+c×8+d+e× 8倍する a×84+b×83+c×82+d×8+e (2) そこで,10進法で書かれた数を8進法で表すには,まず,整数部分と小数部分に分けます. 1) 整数部分は,今まで通りに8進法で表します. 2) 小数部分だけを[1]「8倍して」,[2]「頭を読み取り」,[3]「頭を取り除きます」 (これを繰り返します) ⇒ 右の【例】 |
|
【例8】
(解説)8進法で表された小数7.01(8)を10進法の分数で表してください. 7.01(8)=7+0×+8× =7+=
【例9】
(解説)8進法で表された小数13.7(8)を10進法の小数で表してください. 13.7(8)=1×8+3+7× =8+3+= =11.875
【例10】
(解説)10進法で表された小数12.5を8進法の小数で表してください. (整数部分) 12=1×8+4=14(8) (小数部分)
[1] 8倍すると
小数部分は0.4(8)
(全体で)14.4(8)
0.5×8=4 ←[2]頭の数字は4 [終り] |
|
13.4(8)=1×8+3+4×
=8+3+= →2
3.1(8)=3+1×==3.125 →1
|
|
(整数部分)
21=2×8+5=25(8) (小数部分)
[1] 8倍すると
全体で25.24(8)0.3125×8=2.5 ←[2]頭の数字は2 [3] 2を取り除くと 0.5 [1] 8倍すると 0.5×8=4 ←[2]頭の数字は4 [終り] 小数部分は0.24(8) →3
|
|
【参考:Excelを使った検算】
○Excelには8進数の「正の整数」を10進数の正の整数に変換する関数 =OCT2DEC() がありますが,この関数のままでは8進数の「小数」を10進数の小数に変換することはできません. そこで,3.1を10進数に直すには,
(1) 初めに8倍して「正の整数」に直す.(8進数を1桁繰り上げるには8倍するとよい)
という手順で,8進数の「小数」を10進数の小数に変換できます.→【問題8】の答の検算ができます(2) 次に,これを10進数に変換する. (3) 得られた10進数を8で割る. ○【問題7】のように分数の答が必要なときは,結果が得られてから,Excelの書式設定として書式→セル→分数とすれば分母が3桁までの分数に対応できます. ※ただし,この関数 =OCT2DEC(**) は,引数(**)の値の範囲が**<263168辺りになっているようですので,引数の範囲を超えてしまうときは無理です. |
|
○Excelには10進数の「正の整数」を8進数の正の整数に変換する関数 =DEC2OCT() があります.【例8】のように10進数の「小数」を8進数の小数に変換するには,左欄の逆の手順のように見えますが,割り算を簡単に行うには8, 64, 512..倍して8, 64, 512,..で割るのがよいようです.
(1) 初めに8n倍して「正の整数」に直す.(8, 64, ..とやってみて整数になればよい)
という手順で,10進数の「小数」を8進数の小数に変換できます.(2) 次に,これを8進数に変換する. (3) 得られた8進数を8nで割る.(小数点を動かすだけ) ※ただし,この関数 =DEC2OCT(**) は,引数(**)の値の範囲が**<536870912=229となっているようですので,引数の範囲を超えてしまうときは無理です. ※また,8n倍で整数にならないときは無理です. 【問題9】の場合
(1) 21.3125×64=1364で整数になる.
(2) DEC2OCT(1364)=2524 により,8進数になる. (3) 64で割るから,2桁下げて25.24が答 |
|
16進法で書かれた小数
x,y,z,s,tが0,1,2,...,8,9,A,B,C,D,E,Fの数字であるとき,16進法で書かれた小数xyz.st(16)は
x×162+y×16+z+s×+t× を表します. ただし,Aは10,Bは11,...,Fは15を1文字で表したものとします. ※ 小数第n位の数は,の係数になっています.
○ 10進法で書かれた小数を16進法で表すには,次のように考えると簡単です.
(1) 16進法で書かれた数は,16倍すると左に1桁ずつシフトします. x×162+y×16+z+s×+t× 16倍する x×163+y×162+z×16+s+t× 16倍する x×164+y×163+z×162+s×16+t (2) そこで,10進法で書かれた数を16進法で表すには,まず,整数部分と小数部分に分けます. 1) 整数部分は,今まで通りに16進法で表します. 2) 小数部分だけを[1]「16倍して」,[2]「頭を読み取り」,[3]「頭を取り除きます」 (これを繰り返します) ⇒ 右の【例】 |
|
【例11】
(解説)16進法で表された小数0.1A(16)を10進法の分数で表してください. 0.1A(16)=1×+10× ==
【例12】
(解説)16進法で表された小数12.3(16)を10進法の小数で表してください. 12.3(16)=1×16+2+3× =16+2+= =18.1875
【例13】
(解説)10進法で表された小数32.6875を16進法の小数で表してください. (整数部分) 32=2×16+0=20(16) (小数部分)
[1] 16倍すると
小数部分は0.B(16)
(全体で)20.B(16)
0.6875×16=11 ←[2]頭の数字はB [終り] |
|
3.C(16)=3+12×
=3+= →4
A.8(16)=10+8×=10+==10.5 →2
|
|
(整数部分)
11=B(16) (小数部分)
[1] 16倍すると
全体でB.4(16)0.25×16=4 ←[2]頭の数字は4 [終り] 小数部分は0.4(16) →3
|
|
【参考:Excelを使った検算】
○Excelには16進数の「正の整数」を10進数の正の整数に変換する関数 =HEX2DEC() がありますが,この関数のままでは16進数の「小数」を10進数の小数に変換することはできません. そこで,【問題11】においてA.8を10進数に直すには,
(1) 初めに16倍して「正の整数」に直す.→A8 (16進数を1桁繰り上げるには16倍するとよい
という手順で,16進数の「小数」を10進数の小数に変換できます.→【問題11】の答の検算ができます(2) 次に,これを10進数に変換する.):HEX2DEC("A8")=168 ダブルクォートなしでは,セル番地を参照してしまうので注意 (3) 得られた10進数を16で割る.(=168/16=10.5) ○【問題10】のように分数の答が必要なときは,結果が得られてから,Excelの書式設定として書式→セル→分数とすれば分母が3桁までの分数に対応できます. ※ただし,この関数 =HEX2DEC(**) は,引数(**)の値の範囲が**<231=4294967296あたりになっているようですので,引数の範囲を超えてしまうときは無理です. |
|
○Excelには10進数の「正の整数」を16進数の正の整数に変換する関数 =DECHEX() [Dec To Hex の短縮形]があります.
【例13】のように10進数の「小数」を16進数の小数に変換するには,
(1) 初めに16n倍して「正の整数」に直す.(16, 256, ..とやってみて整数になればよい)
という手順で,10進数の「小数」を16進数の小数に変換できます.(2) 次に,これを16進数に変換する. (3) 得られた16進数を16nで割る.(小数点を動かすだけ) ※ただし,この関数 =DEC2HEX(**) は,引数(**)の値の範囲が**<536870912=229となっているようですので,引数の範囲を超えてしまうときは無理です. ※また,16n倍で整数にならないときは無理です. 【問題12】の場合
(1) 11.25×16=180で整数になる.
(2) DEC2HEX(180)=B4 により,16進数になる. (3) 16で割るから,1桁下げてB.4が答 |