■組分け …《解説》
「順列」「組合せ」は場合の数の数え方，確率の基本として最重要な内容ですが，この頁で扱う「組分け」というのは，組合せに並ぶような位置を占めていません．どちらかというと組合せの応用問題の１つの形に付けられた名前です
【例１】
■基本
９人の人をＡの部屋に４人，Ｂの部屋に３人，Ｃの部屋に２人入れる方法は，9Ｃ4・5Ｃ3・2Ｃ2通り＝1260通りです.
（解説）
■部屋に名前（区別）がある場合--これが基本
全体ＣＡの人数・残りＣＢの人数・さらに残りＣＣの人数
したがって，９人の人を４人，３人，２人の３組に分ける方法は，
9Ｃ4・5Ｃ3・2Ｃ2通り＝1260通りです.
４人の組はＡにしか入れず，３人の組はＢにしか入れず，２人の組はＣにしか入れません.だから，部屋を決める場合と同じになります.
（同様にして）
９人の人をＡの部屋に３人，Ｂの部屋に３人，Ｃの部屋に３人入れる方法は，
9Ｃ3・6Ｃ3・3Ｃ3通り＝1680通りになります.
■単に組に分けるのは，部屋に区別がない場合に対応します
９人の人を３人，３人，３人の３組に分ける方法は，部屋に区別がある場合÷３！です.
３組に分ける方法をx通りとおき，まず組分けをしてから部屋に入れるとすると，x通りの各々について部屋に入れる方法が3!通りあります.
だから，
x＝部屋に区別がある場合（基本）÷3!通り
となります.
⇒ 誰と同じ組になるかということだけに関心がある場合，例えば次の分け方は全部同じ１つの分け方です．
だから，「１つの組分け」に対して「Ａ，Ｂ，Ｃの３つの部屋に入る方法」は3!=6倍あります．
A{1,2,3}, B{4,5,6},
C{7,8,9}
A{1,2,3}, C{4,5,6},
B{7,8,9}
B{1,2,3}, A{4,5,6},
C{7,8,9}
B{1,2,3}, C{4,5,6},
A{7,8,9}
C{1,2,3}, A{4,5,6},
B{7,8,9}
C{1,2,3}, B{4,5,6},
A{7,8,9}
【例２】
■基本 （部屋に区別がある場合）
９人の人をＡの部屋に５人，Ｂの部屋に２人，Ｃの部屋に２人の３組に分ける方法
Ａの部屋に入る５人を選ぶ方法が9Ｃ5=126通り
その各々について，残り４人からＢの部屋に入る２人を選ぶ方法が4Ｃ2=6通り
その各々について，残り２人は自動的にＣの部屋に決まるから１通り
結局，126×6×1=756通り
■応用 （部屋に区別がない場合）
９人の人を５人，２人，２人の３組に分ける方法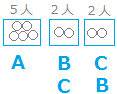
このような組に分ける方法が x通りあるとして，上記の「基本=部屋の区別がある場合」との関係を調べる．
各々の組わけに対して，５人の組は必ずＡの部屋に入る．
次に，２人の組はＢの部屋に入るかＣの部屋に入るか 2!通りある．
だから，「基本=部屋の区別がある場合」は x×2!通り
x×2!=756
x=378
（参考）
部屋に区別がある次の２通りの入り方は，組分けとしては同じものです.
A{1,2,3,4,5}, B{6,7},
C{8,9}
A{1,2,3,4,5}, C{6,7},
B{8,9}
(Ａの部屋とはメンバ入れ替えできません.）
※部屋に区別がある場合 ÷２！と覚えてしまってもよい.
《組分けの要点》
Aの人数= p，Bの人数= q，Cの人数= r，合計= nとするとき
基本は
nCp×n−pCq×n−p−qCr
p+q+r=n → n−p−q=rだから３個目の式は
n−p−qCr=rCr=1
になる．
（Cの部屋に入れる方法は，残った人に自動的に決まってしまう）
組に名前がなく， ３組の人数が同じときは， 基本÷ ３！通り
組に名前がなく， ２組の人数が同じときは， 基本÷ ２！通り
【例３】
８人の人を次の組に分ける方法は各々何通りあるか
(1) ４人，４人の２組に分ける場合
 …（答）
(2) ３人，３人，２人の３組に分ける場合
 …（答）
(3) ２人，２人，２人，２人の４組に分ける場合
 …（答）
(4) ５人，２人，１人の３組に分ける場合
 …（答）
※(4)の問題は，同じ人数の組がないので，部屋に名前が付いている場合とまったく同じ結果になります．すなわち，Aの部屋に５人，Bの部屋に２人，Cの部屋に１人入れる方法と同じです．
|
...�域声蟶ｯ迚茨ｼ峨Γ繝九Η繝ｼ縺ｫ謌ｻ繧�