組合せ

{A, B}　{A, C}　{B, C}

※要素の順序を区別しない組は「中かっこ」{ 　}を使って表すのが普通です．「中かっこ」{ 　}は，その中に書かれている要素の順序を区別せず，何が入っているかだけを問題にし，どの順に書かれているかを問題にしていないので {A, B}　は　{B, A}　と同じです．
○　だから，「組合せ」を数えるときに {A, B}を数えたら，もう{B, A}は数えません．
{A, B}を数えてから，さらに{B, A}も数えたら，同じものを２回数えていることになります．

日常生活に登場する例で言えば，Aチーム対Bチームの試合が済んだときに，「いやまだ，Bチーム対Aチームの試合は済んでいない」などと考える人はいません．試合の相手は「組合せ」で決まるので，書き方の順序を区別せずに数えます．

○　同様にして，{A, C}の組を数えたら，もう{C, A}の組を数える必要はありません．
○　同様にして，{B, C}の組を数えたら，もう{C, B}の組を数える必要はありません．

⇒このようにして，「異なる3個の文字 {A, B, C} から，異なる2個の文字を選ぶ組合せ」は，初めに書いた3通りあることになります．

一般に「異なるn個のものから，異なるr個のものを選ぶ組合せ」の総数はn C rで表されます．
上記の結果は，
3C2=3
と書かれます．

ところで，上の解説では，

「異なる3個の文字 {A, B, C} から，異なる2個の文字を選ぶ組合せ」の総数

を１つずつ全部調べて数えましたが，

「異なる3個の文字 {A, B, C} から，異なる2個の文字を選ぶ順列」の総数

の方は，次のように簡単に計算できます．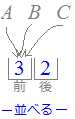

　前の箱に入れる方法の総数は，A,B,C の３通り
　その各々について，後の箱には前に使ったもの以外の２通り
したがって，3×２＝6通り
これを順列の記号を使って表わすと，
3P2=6
と書かれます．

このように「順列の総数 nPr」は，積の法則で簡単に求められるので，「組合せの総数nCr」を「順列の総数」から逆算する公式を作れば計算が楽になります．

組合せ{A, B} ←→ 順列ABとBAが対応する
組合せ{A, C} ←→ 順列ACとCAが対応する
組合せ{B, C} ←→ 順列BCとCBが対応する

2個並べる順列にするときは，2個の要素からなる１つの組合せ×２!の並べ方があるので
3P2=3C2×2!
つまり
$_3 C _2=\frac{_3 P _2}{2!}$ $(3=\frac{6}{2})$
で求められることになります．

から3個とって並べる方法

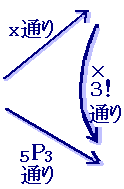
3個選ぶ方法の例

上の例を並べる方法

□　記号
　異なるｎ個のものから，異なるｒ個のものを選ぶ組合せの総数を_ｎＣ_ｒで表します.上の例は，５個のものから３個選ぶ組合せの総数となっているので，
$_5 C _3=\frac{_5 P _3}{3!}$
となります.

《要点》
　一般に，異なるｎ個のものから異なるｒ個のものを選ぶ方法 $_n C _r$ をxとおくと
$x\times r!=_n P _r$
となるので
$x=\frac{_n P _r}{r!}$
となります．

《公式》
$_n C _r=\frac{_n P _r}{r!}$
$=\frac{n!}{(n-r)!r!}$

異なるｎ個のもの｛1,2,3, ... ,n ｝から，０個取ってくる（何も取ってこない）組合せは

空集合∅＝｛　｝が１種類だけある．

異なるｎ個のもの｛1,2,3, ... ,n ｝から，ｎ個取ってくる（全部取ってくる）組合せは

全部入っている集合｛1,2,3, ... ,n ｝が１種類だけある．

ということに対応しています．

（ルール：左の式を一つクリックし，続けて答をクリックしたとき，合っていれば消えます．
･･･間違ったときは，ヒントを読む場合も読まない場合もやり直すボタンを押せば再開できます．

$_4 C _0=\frac{4!}{4!0!}=1$

$_6 C _2=\frac{6!}{4!2!}=15$

$_7 C _6=\frac{7!}{1!6!}=7$

$_8 C _4=\frac{8!}{4!4!}=70$

$_9 C _2=\frac{9!}{7!2!}=36$

$_7 C _3=\frac{7!}{4!3!}=35$

$_5 C _2=\frac{5!}{3!2!}=10$

$_8 C _1=\frac{8!}{7!1!}=8$

$_6 C _5=\frac{6!}{1!5!}=6$

$_{10} C _5=\frac{10!}{5!5!}=252$

とてもわかりやすくて問題もスラスラ解けました！これからも使わせてもらいます！
＝＞［作者］：連絡ありがとう．

赤玉3個、白玉3個入った袋（赤玉、白玉はそれぞれ区別がつかない）から2個取り出す組み合わせについて質問したいです。組み合わせの定義から6C2だと思う一方、この6C2の意味が6P2という順列を重複分の2!で割っていると考えると赤玉3個と白玉3個をそれぞれ区別して考えていることになると思うのですが、どうして赤玉、白玉を区別して考えていいのでしょうか。もしくは、根本的に考え方が間違っていたら訂正してもらいたいです。お願いします。
＝＞［作者］：連絡ありがとう．まず初めに組合せの公式の前提を確かめておきますと

（相）異なるｎ個のものから，（相）異なるｒ個のものを取り出して作れる組合せの総数はnCr…(1)
ご質問のように（赤玉、白玉はそれぞれ区別がつかない）場合は，この公式の前提を満たしていませんので別の数え方になります．
また，異なるｒ個の代わりに，同じものを何回も取り出してくるような場合も別の数え方になります．

ところで，場合の数（順列，組合せなど）と確率を続けて習うときに，場合の数では「ものに区別がない場合」も登場しますが，高校の確率では通常「ものが区別できる場合」しか扱いません．
ここから先は，学習指導要領や教科書・参考書にはっきりと書いたものがなくて筆者独自の考えですが，これは扱っているものの性質によります．すなわち，巨視的な（人の目に見えるレベルの大きさの）ものは「どんなによく似ていても」区別できるものとして計算しなければなりません．･･･日本の造幣局が作った10円硬貨の新品が３個あるような場合でも，確率の計算をするときは必ず別物として数えなければなりません（そうしないと現実と合わない）．これに対して，ミクロの世界では，光の粒子を数えるときに全く同じものがあるとして成り立つ確率があります．
このように実際の世界では，ものが区別できるかどうかはそのものの性質によります．数学では初めに約束を決めておいてから，どちらの場合も取り扱いますが，その結果は初めの約束によって変わることになります．

さて，元の問題に戻りますと，赤玉3個、白玉3個入った袋（赤玉、白玉はそれぞれ区別がつかない）から2個取り出す組み合わせは，赤赤，赤白，白白の３通りでしょう．（組合せだから白赤は別に数え上げないでしょう）．…(2)
･･･はじめに（赤玉、白玉はそれぞれ区別がつかない）と書いてあるからです．
間違ってはいけないのは，確率の問題をやっているときにはこの計算は使えないということです．すなわち，大きさ形重さが全く同じで区別のつかない赤玉3個、白玉3個から２個取り出すとき，赤玉２個が出る確率は
$p=\frac{_3C_2}{_6C_2}=\frac{1}{5}$
でしょう．間違っても
$p=\frac{1}{3}$
と答えてはいけません．なぜなら，高校の数学に登場するのは，人の目に見える程度の大きさのものだからです．

果物の図がかなりわかりやすい。このサイト見たからks分からないがいつもより数学の点数高かった
＝＞［作者］：連絡ありがとう．連絡をもらったらその頁を見るようにしていますが，ふと見ると，プログラムミスで正解した後に次の選択ができなくなっていましたので訂正しました．