組合せ
《解説》
■　並べ方を区別するのが「順列」で，並べ方を区別しないのが「組合せ」です.
■　異なる５個のくだものから，異なる３個のくだものを選ぶ（選ぶだけで並べない）組合せは，次のように，順列から逆算すると分かります.

から3個とって並べる方法
3個選ぶ方法の例



上の例を並べる方法
　　　　　
　　　　　
　　　　　

 
　

■　３個選んで並べる方法は，5P3＝５・４・３通り

■　他方，この操作を2段階に分けて，まず３個選ぶ方法が，求めるべきｘ通り
　その各々について，３個のものの並べ方は３！通り
　したがって，３個選んで並べる方法はｘ・３！通り
■　以上の２つは等しいはずだから，ｘ・３！＝5P3
　ゆえに，ｘ＝5P3／３！通り
□　記号
　異なるｎ個のものから，異なるｒ個のものを選ぶ組合せの総数をｎＣｒで表します.上の例は，５個のものから３個選ぶ組合せの総数となっているので，5Ｃ3＝5P3/３！となります.

《要点》
　一般に，異なるｎ個のものから異なるｒ個のものを選ぶ方法は，
ｎＣｒをｘとおくと，
ｘ・ｒ！＝ｎＰｒとなるので，
ｘ＝ｎＰｒ／ｒ！となります.
 《公式》
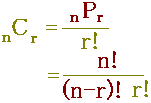■　例
　異なる4個のものから，異なる2個のものを選ぶ組合せの総数は，４Ｃ２＝4！／(2!2!)＝6通り・・・(答)
■　重要な例
　どんなｎ（＞1）の値についても，ｎＣ０＝1，ｎＣｎ＝1が成り立ちます.（理由：　ｎＣ０＝ｎ！／(ｎ！０！)＝1　また　ｎＣｎ＝ｎ！／(０！ｎ！)＝1　）


《問題》　左の値に等しいものを，右から選びなさい．
（ルール：左の式を一つクリックし，続けて答をクリックしたとき，合っていれば消えます．間違えば「♪〜ふりだしに戻る〜♪」．）




















 
 

←メニューに戻る　↑問題の順序を変えて，もう一度する