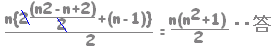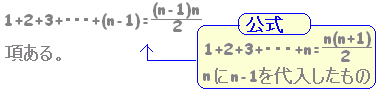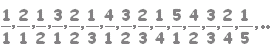【問題5】
数列
 \( \displaystyle \frac{1}{1}\hspace{0px},\hspace{0px}\frac{1}{2}\hspace{0px},\hspace{0px}\frac{2}{2} \) \( \displaystyle \frac{1}{1}\hspace{0px},\hspace{0px}\frac{1}{2}\hspace{0px},\hspace{0px}\frac{2}{2} \) \( \displaystyle ,\hspace{0px}\frac{1}{3}\hspace{0px},\hspace{0px}\frac{2}{3}\hspace{0px},\hspace{0px}\frac{3}{3}\hspace{0px},\hspace{0px}\cdots, \) \( \displaystyle ,\hspace{0px}\frac{1}{3}\hspace{0px},\hspace{0px}\frac{2}{3}\hspace{0px},\hspace{0px}\frac{3}{3}\hspace{0px},\hspace{0px}\cdots, \) \( \displaystyle \hspace{0px}\frac{1}{n}\hspace{0px},\hspace{0px}\frac{2}{n}\hspace{0px},\hspace{0px}\cdots\hspace{0px},\hspace{0px}\frac{n-1}{n}\hspace{0px},\hspace{0px}\frac{n}{n},\hspace{0px}\cdots \) \( \displaystyle \hspace{0px}\frac{1}{n}\hspace{0px},\hspace{0px}\frac{2}{n}\hspace{0px},\hspace{0px}\cdots\hspace{0px},\hspace{0px}\frac{n-1}{n}\hspace{0px},\hspace{0px}\frac{n}{n},\hspace{0px}\cdots \)
を次のような群に分ける.
 \( \displaystyle \frac{1}{1}\mid\frac{1}{2},\frac{2}{2} \) \( \displaystyle \frac{1}{1}\mid\frac{1}{2},\frac{2}{2} \) \( \displaystyle \mid\frac{1}{3},\frac{2}{3},\frac{3}{3}\mid\cdots \) \( \displaystyle \mid\frac{1}{3},\frac{2}{3},\frac{3}{3}\mid\cdots \) \( \displaystyle \mid\frac{1}{n},\frac{2}{n},\cdots,\frac{n-1}{n},\frac{n}{n}\mid\cdots \)
第1群第2群第3群第n群 \( \displaystyle \mid\frac{1}{n},\frac{2}{n},\cdots,\frac{n-1}{n},\frac{n}{n}\mid\cdots \)
第1群第2群第3群第n群
(1) 第28群に入るすべての項の和を求めよ.
(2) 第 n群の最初の数が第何項かを求めよ.
(3) 第2016項を求めよ.
(2016年度滋賀大入試問題)
解説を読む
解説を隠す
(1) 第28群の項は,分母が28で分子は1から28まであるから,その和は
 \( \displaystyle \frac{1}{28}\times\frac{28\times 29}{2}=\frac{29}{2} \) \( \displaystyle \frac{1}{28}\times\frac{28\times 29}{2}=\frac{29}{2} \)
(2) 第 n−1群の末尾までには
n}{2}&chco=660000) \( \displaystyle \frac{(n-1)n}{2} \)項あるから \( \displaystyle \frac{(n-1)n}{2} \)項あるから
第 n群の最初の数は
第 \( \displaystyle \frac{n^2-n+ 2}{2} \)項 \( \displaystyle \frac{n^2-n+ 2}{2} \)項
(3) 第 n群の末尾までには, }{2}&chco=660000) \( \displaystyle S_n=\frac{n(n+1)}{2} \) \( \displaystyle S_n=\frac{n(n+1)}{2} \)項ある.
※2016年度の入試問題だから,受験生に束の間のジョークとして第2016項と言ってみた?
これで笑える人は,余裕あるな〜♪
 \( \displaystyle S_{63}=\frac{63\times 64}{2}=2016 \) \( \displaystyle S_{63}=\frac{63\times 64}{2}=2016 \)
であるから,初めから数えて2016項は,第63群の最後の項.
 \( \displaystyle \frac{63}{63} \)
…(答) \( \displaystyle \frac{63}{63} \)
…(答)
|