■　回答集計と各ページの分析
***　【回答集計と分析・高校】　***
数I/ 数A/ 数II/ 数B/ 数III/ 数C/
［測定条件と信頼性］
■中学２年■　== 式の計算1 ==
■ページ名 「多項式の和差」
../math/siki01.htm
■主な内容 　多項式において同類項をまとめて簡単にするもの．かっこをはずす操作を含む．
■要約・解説 ８行「最初の問題に着手するまでの時間」は19秒でこの解説はチラリと見た程度．
■この集計の作成年月日：2009.10.23　■集計期間2009.05.05〜2009.10.21　■期間中のこのペ−ジに対するアンケート回答数/読まれた回数：177件/6504件=1.9%（時間に関する集計は極端値を除く）
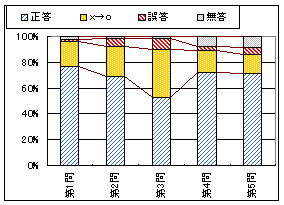
グラフ1

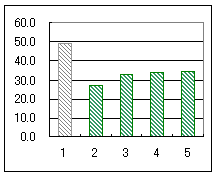
グラフ2

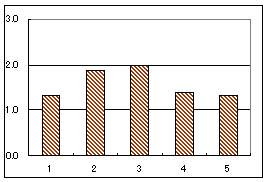
グラフ3
■小問数
5題

■ヒント
なし

■入力方式
空欄書き込み

■問題の見え方
一度に全部見える形になっている		 回答者の内訳は中2が60%，卒業生が23%
１題当たりの所要時間は32秒．
　左のグラフ１は問題ごとの正答，誤答，無答の割合（正誤は最初の採点）で，黄色で示したものは初め誤答で再試行の結果正答に変った割合を表わす．
　グラフ2は横軸が問題番号，縦軸は直前の操作以降その問題の採点までの経過時間（秒）を表わす．ただし，第1問は初めからの時間．
　グラフ3は問題ごとの試行回数を表わす．（ただし，同一問題を16回以上試行した答案については16回と見なす．）
表1は各問題の得点と残りの問題の合計得点との相関係数（I-R相関係数）で，第1問，第3問が0.2未満となり，これらの結果に学力以外の要因が混入している可能性がある．
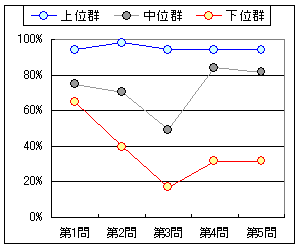
　また，グラフ４は合計得点によって回答者を上位群，下位群（各27%），中位群（残り）に分けたときの問題別正答率である．
　これによれば，第4問，第5問における中位群の正答率は「やさしい問題」における自然な値を示しているが，第1問における中位群の正答率が不自然な位置にある．
　第1問は先頭の問題としての戸惑いからイレギュラーな結果となることがある．第2問，第3問では，空欄の数やその前にマイナスがあるかどうかなど入力方式の違いによる戸惑いが誤答の要因となることが考えられる．
主な誤答
第1問：7x11y←演算記号の＋を書いていない
第2問：-2a+9b, -2a-9b←かっこの外し方
第3問：4, 8 , 8←4 が違う
学習開始時において平均正答率は60%台で，多くの回答者はこの頁の内容を処理できる．
この頁の学習により，正答率は68.6%から90.8%へ変化し，ここで扱った項目に関して22.3%の成績アップが見込まれる．
表１
I-R
相関係数		 第1問 第2問 第3問 第4問 第5問
0.07 0.22 0.19 0.31 0.36
グラフ4

■ページ名 「かっこをはずす」
../math/moji003.htm
■主な内容 　等式の変形の基本として，かっこをはずすもの
■要約・解説 なし「最初の問題に着手するまでの時間」は1.1秒．やり方は直ちに理解できたと考えられる．
■この集計の作成年月日：2009.10.17　■集計期間200.05.06〜2009.10.10　■期間中のこのペ−ジに対するアンケート回答数/読まれた回数：61件/2830件=2.2%（時間に関する平均は極端値を除く）
グラフ1

グラフ2
■小問数
10題

■ヒント
なし

■入力方式
マウス選択
（多対多）

■問題の見え方
一度に全部見える形になっている		 回答者の内訳は，中2が43%，卒業生が31%
１題当たりの所要時間は5.9秒．
※　問題の順序はランダムで１つの画面に表示されているものは元の番号と同じではない．
　元の番号は，次の通り．
第1問 -(2x-7)
第2問 3(2x-3)
第3問 -2(x+3)
第4問 3(2x+5)
第5問 -3(2x-5)
第6問 -2(x-6)
第7問 2(3x-2)
第8問 -3(2x+3)
第9問 -2(x-7)
第10問 2(x-7)
　左のグラフ１は問題ごとの正答，誤答，無答の割合（正誤は最初の採点）で，黄色で示したものは初め誤答で再試行の結果正答に変った割合を表わす．
　グラフ2は横軸が問題番号，縦軸は直前の操作以降その問題の採点までの経過時間（秒）を表わす．ただし，第1問は初めからの時間．
　グラフ3は問題ごとの試行回数を表わす．（ただし，同一問題を16回以上試行した答案については16回と見なす．）
どの問題の正答率も概ね80%以上でよくできている．正答率の凹凸は誤算の範囲であると考えられる．
　第5問のような -○(△x-□)の形は，所要時間が約2倍になっている．
　学習開始時において平均正答率は80%台で，この頁の問題は回答者にとって「非常にやさしい」部類に入る．
この頁の学習により，正答率は87.0%から97.4%へ変化し，ここで扱った項目に関して10.3%の成績アップが見込まれる．
グラフ3

■ページ名 「式の加法減法（かっこをはずす2）」
../math/moji004.htm
■主な内容 　等式の変形の基本として，かっこをはずすもの
■要約・解説 なし「最初の問題に着手するまでの時間」はほぼ0秒．
■この集計の作成年月日：2009.10.23　■集計期間2009.05.05〜2009.10.18　■期間中のこのペ−ジに対するアンケート回答数/読まれた回数：32件/2337件=1.4%（時間については極端値を除く）
グラフ1

グラフ2

グラフ3
■小問数
8題

■ヒント
なし

■入力方式
マウス選択
（多対多）

■問題の見え方
一度に全部見える形になっている		 回答者の内訳は，中1が16%，中2が47%，中3が9%，卒業生が19%
１題当たりの所要時間は16秒．
　左のグラフ１は問題ごとの正答，誤答，無答の割合（正誤は最初の採点）で，黄色で示したものは初め誤答で再試行の結果正答に変った割合を表わす．
　グラフ2は横軸が問題番号，縦軸は直前の操作以降その問題の採点までの経過時間（秒）を表わす．ただし，第1問のみは推定．
　グラフ3は問題ごとの試行回数を表わす．（ただし，同一問題を16回以上試行した答案については16回と見なす．）
※　問題は順不同で表示され，画面に表示されているものは元の番号と同じではない．
　元の番号は，たとえば次の通り．
第5問 4(a-b)-2(a-3b)
第6問 3(x+3y)-5(x-2y)
第7問 2(5x+y)-3(x-2y)
第8問 5(2a+3b)-2(a+3b)
よく似た問題であり，問題間で正答率の差異は少ない．
　表1は各問題の得点と残りの問題の合計得点との相関係数（I-R相関係数）で，どの問題も r > 0.5 となり，回答者から見ても同質の問題であることが示される．
　グラフ4は合計得点によって回答者を上位群，下位群（各27%），中位群（残り）に分けたときの問題別正答率である．これによれば，どの問題でも中位群は上位群と近くやさしい問題であったことが分かる．また識別力が非常に高く，ほぼ全問正答となる上位群+中位群と大部分の問題で誤答・無答となる下位群にはっきりと分かれる．
学習開始時において平均正答率は80%台で，ほとんどの回答者はこの頁の問題ができる．
この頁の学習により，正答率は80.9%から93.8%へ変化し，ここで扱った項目に関して12.9%の成績アップが見込まれる．
表１
I-R
相関係数		 第1問 第2問 第3問 第4問 第5問 第6問 第7問 第8問
0.80 0.75 0.56 0.75 0.82 0.73 0.88 0.63
グラフ4

■ページ名 「かっこでくくる」
../math/moji002.htm
■主な内容 　等式の変形の基本として，かっこでくくるもの（高校数学で重要となるｘ2の係数でくくる変形を中心に扱う）
■要約・解説 なし「最初の問題に着手するまでの時間」はほぼ0秒．
■この集計の作成年月日：2009.10.23　■集計期間2009.06.25〜2009.10.17　■期間中のこのペ−ジに対するアンケート回答数/読まれた回数：18件/861件=2.1%
グラフ1

グラフ2

グラフ3

表１
I-R
相関係数　		 第1問 第2問 第3問 第4問 第5問 第6問 第7問 第8問 第9問 第10問
0.62 0.62 0.46 0.80 0.47 0.80 0.38 0.40 -0.01 0.22
■小問数
10題

■ヒント
なし

■入力方式
マウス選択
（多対多）

■問題の見え方
一度に全部見える形になっている		 回答者の内訳は，中1が33%，中2が17%，中3が0%，卒業生が44%
１題当たりの所要時間は6秒．
　左のグラフ１は問題ごとの正答，誤答，無答の割合（正誤は最初の採点）で，黄色で示したものは初め誤答で再試行の結果正答に変った割合を表わす．
　グラフ2は横軸が問題番号，縦軸は直前の操作以降その問題の採点までの経過時間（秒）を表わす．ただし，第1問は初めからの時間．
　グラフ3は問題ごとの試行回数を表わす．（ただし，同一問題を16回以上試行した答案については16回と見なす．）
※　問題は順不同で表示され，画面に表示されているものは元の番号と同じではない．
　元の番号は，たとえば次の通り．
第3問 -x2-6x
第6問 -2x2+6x
第8問 3x2-6x
第9問 -3x2-6x
第10問 -3x2+6x
表1は各問題の得点と残りの問題の合計得点との相関係数（I-R相関係数）で，ほとんどの問題で整合性が認められるが，第9問が異常になっている．
　グラフ4は合計得点によって回答者を上位群，下位群（各27%），中位群（残り）に分けたときの問題別正答率である．これによれば第9問で中位群が上位群を上回る逆転が生じている．
　以上２つのデータから，第9問は学力による正誤以外にマグレによる正誤が発生しやすいと考えられる．（原因は分からない）
　通常ならばこの問題を差し替えるべきであるが，偶然が重なったものかどうか確かめる必要がありしばらくこのまま使う．
学習開始時において平均正答率は80%台で，ほとんどの回答者はこの頁の問題ができる．
この頁の学習により，正答率は81.1%から95.6%へ変化し，ここで扱った項目に関して14.4%の成績アップが見込まれる．
グラフ4

■ページ名 「文字式の計算」
../math2/kakko1.htm
■主な内容 　x,y ２文字を含む式のかっこをはずすもの
■要約・解説 なし「最初の問題に着手するまでの時間」は2.8秒．
■この集計の作成年月日：2009.10.24　■集計期間2009.05.03〜2009.10.20　■期間中のこのペ−ジに対するアンケート回答数/読まれた回数： 55件/1850件=3.0%
グラフ1


グラフ2

グラフ3

表1
I-R
相関		 第1問 第2問 第3問 第4問 第5問 第6問 第7問 第8問 第9問 第10問
0.71 0.73 0.78 0.81 0.76 0.60 0.77 0.76 0.72 0.75
グラフ4
■小問数
10題

■ヒント
なし

■入力方式
マウス選択
（多対多）

■問題の見え方
一度に全部見える形になっている		 解答者の内訳は，中1が31%，中2が33%，中3が0%，卒業生が20%
１題当たりの所要時間は18秒
平均滞在時間は6分5秒
　左のグラフ１は問題ごとの正答，誤答，無答の割合（正誤は最初の採点）で，黄色で示したものは初め誤答で再試行の結果正答に変った割合を表わす．下のグラフは，正答率の通常の定義に従って解答者を分母とした割合で示したもの．
　グラフ2は，横軸が問題番号，縦軸は直前の操作以降その問題の採点までの経過時間（秒）を表わす．ただし，第1問は初めからの時間．
　グラフ3は問題ごとの試行回数を表わす．（ただし，同一問題を16回以上試行した答案については16回と見なす．）
画面上，問題と選択肢はランダムに表示されるが，左の集計は元の問題番号についてのものである．
　また，画面の設定上「ふりだしに戻った」場合にも初回の正誤は引き継がれる．
信頼性・識別力について
表1は各問題の得点と残りの問題の合計得点との相関係数（I-R相関係数）で，いずれも非常に高く，整合性が認められる．
　グラフ4は合計得点によって回答者を上位群，下位群（各27%），中位群（残り）に分けたときの問題別正答率を示す．
　これによれば，どの問題も識別力が高く，第5問，第6問，第8問において中位群が上位群に接近していることからこれらの問題はやさしいと受け止められたことが分かる．
誤答の要因について
　表1は問題の形と無答を除く誤答率の一覧で，これによって問題の形と誤答率の相関を求めたものが表2である．表2によれば，「かっこ内のマイナスの個数」は誤答にあまり影響しておらず「かっこ外のマイナスの個数」「マイナスの総数」との相関が高いことが分かる．
　誤答の要因として「かっこ外のマイナスの個数」「マイナスの総数」の２つを想定して重重回帰分析を行うと，誤答の63%が説明でき，ここにない形の問題，例えば
　　　　-2(3x-y)-3(x+2y)
の誤答率は27%と予想される．
学習開始時において平均正答率は60%台で，多くの回答者はこの頁の問題を処理できる．
この頁の学習により，正答率は69.8%から77.6%へ変化し，ここで扱った項目に関して7.8%の成績アップが見込まれる．
表2
　 第1問 第2問 第3問 第4問 第5問 第6問 第7問 第8問 第9問 第10問
かっこ外
のマイナス		 1 1 0 1 0 1 1 1 1 2
かっこ中
のマイナス		 0 2 2 2 2 0 1 2 2 3
マイナス計 1 3 2 3 2 1 2 3 3 5
誤答率 22% 16% 12% 24% 12% 12% 24% 21% 24% 28%
表3
誤答率
との相関		 外のマイナス 中のマイナス マイナス計
0.77 0.28 0.60

■ページ名 「文字の計算」
../math/moji001.htm
■主な内容 　文字式を計算して簡単にするもの
■要約・解説 なし「最初の問題に着手するまでの時間」は1.9秒．
■この集計の作成年月日：2009.10.27　■集計期間2009.06.17〜2009.10.20　■期間中のこのペ−ジに対するアンケート回答数/読まれた回数： 60件/1891件=3.2%
グラフ1

グラフ2

グラフ3

表1
　 第1問 第2問 第3問 第4問 第5問 第6問 第7問 第8問 第9問 第10問
文字数 2 1 2 2 2 2 1 1 1 1
かっこ外のマイナス 0 0 1 0 1 0 0 0 0 0
誤答率 33% 18% 38% 23% 33% 25% 32% 32% 22% 18%
表2
誤答率
との相関		 文字数 かっこ外のマイナス
0.47 0.62
■小問数
10題

■ヒント
なし

■入力方式
マウス選択
（多対多）

■問題の見え方
一度に全部見える形になっている		 解答者の内訳は，中1が65%，中2が22%，中3が2%，卒業生が10%
１題当たりの所要時間は8秒
平均滞在時間は8分33秒
　左のグラフ１は問題ごとの正答，誤答，無答の割合（正誤は最初の採点）で，黄色で示したものは初め誤答で再試行の結果正答に変った割合を表わす．下のグラフは，正答率の通常の定義に従って解答者を分母とした割合で示したもの．
　グラフ2は，横軸が問題番号，縦軸は直前の操作以降その問題の採点までの経過時間（秒）を表わす．ただし，第1問は初めからの時間．
　グラフ3は問題ごとの試行回数を表わす．（ただし，同一問題を16回以上試行した答案については16回と見なす．）
画面上，問題と選択肢はランダムに表示されるが，左の集計は元の問題番号についてのものである．
誤答の要因について
　表1は問題の形と（無答を含む）誤答率の一覧で，これによって問題の形と誤答率の相関を求めたものが表2である．表2によれば，「文字数」「かっこ外のマイナス」のいずれも誤答に影響していると考えられる．
（ただし，さらに重回帰分析を行うとこれら２つの要因で説明できる誤答は誤答全体の42%となり，それ以外の偶然的な要因も大きい･･･簡単な選択問題であるから）
信頼性・識別力について
表3は各問題の得点と残りの問題の合計得点との相関係数（I-R相関係数）で，いずれも非常に高く，整合性が認められる．
　グラフ4は合計得点によって回答者を上位群，中位群，下位群（各33%）に分けたときの各群の問題別正答率を示す．
　これによれば，どの問題も識別力が高く，第2問，第4問，第6問，第9問，第10問において中位群が上位群に接近していることからこれらの問題はやさしいと受け止められたことが分かる．
学習開始時において平均正答率は70%台で，多くの回答者はこの頁の問題を処理できる．
この頁の学習により，正答率は72.5%から87.3%へ変化し，ここで扱った項目に関して14.8%の成績アップが見込まれる．
表3
I-R
相関		 第1問 第2問 第3問 第4問 第5問 第6問 第7問 第8問 第9問 第10問
0.63 0.56 0.52 0.67 0.68 0.89 0.73 0.56 0.77 0.59
グラフ4

○===メニューに戻る