分母に根号のない形

【分母に根号がない形とは】

$\frac{1}{\sqrt{2}}$ を $\frac{\sqrt{2}}{2}$ に書き直したり， $\sqrt{\frac{3}{2}}$ を $\frac{\sqrt{6}}{2}$ に書き直えることを「分母に根号がない形」にするといいます．

（解説）

　 $\frac{1}{\sqrt{2}}$ よりは， $\frac{\sqrt{2}}{2}$ の方が便利な事があります．
　【例１】　この数字のだいたいの大きさを求めるために， $\sqrt{2}=1.41421356\cdots$ を使って割り算をしようと考えた場合，

$1.4\overline{)1.0}\rightarrow 14\overline{)10}$
$1.41\overline{)1.00}\rightarrow 141\overline{)100}$
$1.414\overline{)1.000}\rightarrow 1414\overline{)1000}$
のように「小数点を移動」して割り算を始めようとしても， $1.41421356\cdots$ が無限小数になっているので，1000倍しても10000倍しても計算が始められません．
$1.41421356\cdots \overline{)1.000\cdots}\rightarrow ??$

　これに対して $\frac{\sqrt{2}}{2}$ の形を使えば
$2\overline{)1.41421356\cdots }\rightarrow 0.7071\cdots}$
のように前から順に必要な桁数だけ求めることができます．

　【例２】　文字式で $2x + \frac{3}{x}$ のような式は文字の部分が同じとは言えないので，係数をまとめて簡単にすることができません．

これと同様に
$2\sqrt{2} + \frac{3}{\sqrt{2}}$
のような形をしていると， $\sqrt{2}$ の係数をまとめて簡単にすることができませんが，
$2\sqrt{2} + \frac{3}{2}\sqrt{2}$
の形になっていると
$(2 + \frac{3}{2})\sqrt{2}=\frac{7}{2}\sqrt{2}$
と簡単にすることができます．

※このように，さまざまな計算の中に $\sqrt{2}$ のような根号があるときは，分母に根号がない形に変形した方が計算しやすいことがあります．特に，足し算や引き算の中に根号が含まれているときは，分母に根号がない形が使いやすくなります．
※分母に根号がない形に変形すると，分子に根号が登場するのが普通ですが，「分子に」根号があるのは「横に」根号があるのと同じで，よい形なのです．
$\frac{\sqrt{2}}{2}\rightarrow\frac{1}{2}\sqrt{2}$
$\frac{2\sqrt{5}}{3}\rightarrow\frac{2}{3}\sqrt{5}$

「分母に根号がない形」あるいは「分母に根号を含まない形」に変形することを，高校では「分母の有理化」といいますが，この用語は中学校の教科書には出ていないようです．（高校でもう一度習います）．
$\sqrt{2}$ のような根号の付いている数を無理数といい，整数や整数の比で書かれる分数は有理数と呼ばれます．そこで，この頁で述べている内容は，分母を無理数から有理数に変えることなので「分母の有理化」とも呼ばれます．

次の項目

【例】
(1)　 $\frac{1}{\sqrt{2}}$ (2)　 $\frac{1}{2\sqrt{3}}$ (3)　 $\frac{3}{\sqrt{20}}$ (4)　 $\sqrt{\frac{4}{5}}$

(1) $\frac{1}{\sqrt{2}}$ のように分母に根号のある式を正しく変形して，分母に根号のない形にするには「分母と同じものを」分母と分子の両方に掛けます．

$\frac{1}{\sqrt{2}}=\frac{1\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}=\frac{\sqrt{2}}{2}$ …（答）

○中学校で習う「根号」は２乗すればその中に書かれた数を表すようになっています．
≪例≫ $(\sqrt{2})^2=2$ ， $(\sqrt{3})^2=3$ ， $(\sqrt{5})^2=5$

　そこで，「分母に書かれた根号と同じ数を掛けると根号がはずれる」というのが，分母から根号を取り除くための基本的な考え方です．

　だから，要点は簡単で，分母に $\sqrt{2}$ があれば $\sqrt{2}$ を掛ける，分母に $\sqrt{3}$ があれば $\sqrt{3}$ を掛ける，分母に $\sqrt{5}$ があれば $\sqrt{5}$ を掛けるとなります．

○しかし，分母だけに勝手に $\sqrt{2}$ などを掛けると，分数の値が変わってしまって，等しい変形にはなりませんので，分母と分子に同じ数を掛けなければなりません．
　この変形は，小学校以来，通分や約分のときに学んで来た変形です．
$\frac{1}{\sqrt{2}}=\frac{1\times a}{\sqrt{2}\times a}$ （← $a=\sqrt{2}$ とする）
$\frac{1}{\sqrt{3}}=\frac{1\times a}{\sqrt{3}\times a}$ （← $a=\sqrt{3}$ とする）

○分母を根号のない形にするためには，分子にも根号を掛けなければなりません．そうすると分子が根号のある形になります．これは仕方のないことです．
　分母をきれいにするためには，分子がボロボロになってもよい．「分母を助けるために分子には泣いてもらう」と割り切ること．両方によい顔をしようなどと中途半端に気を使うと間違ってしまう．

(2) $\frac{1}{2\sqrt{3}}$ のように分母が「根号のない数」と「根号のある数」の積になっている場合

▲次の答案は間違いではないが，このように書くと「この子は勉強をしていない」とばれてしまうので，できれば避けた方がよい．
$\frac{1}{2\sqrt{3}}=\frac{1\times 2\sqrt{3}}{2\sqrt{3}\times 2\sqrt{3}}=\frac{2\sqrt{3}}{12}=\frac{\sqrt{3}}{6}$

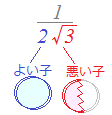⇒「初めに」分母と分子に２も一緒に掛けてしまって，「最後に」２で約分するのなら，無駄な作業を２回行っていることになります．初めから２は掛けないようにすべきです．

$2$ はよい子なので，そのままで使えます．片方（本当は半分ではなくルートだが言いにくいので通俗的に）しかなくて悪い子は $\sqrt{3}$ だけです．
だから，下に書いた答案のように，片方しかない $\sqrt{3}$ だけをもう一枚付けて $3$ の１枚にするのです．

◎お薦めの答案
$\frac{1}{2\sqrt{3}}=\frac{1\times \sqrt{3}}{2\sqrt{3}\times \sqrt{3}}=\frac{\sqrt{3}}{6}$ …（答）

(3) $\frac{3}{\sqrt{20}}$ のように分母の根号が簡単になる場合は，初めに根号を簡単にしてから，次に分母の処理をします．

$\frac{3}{\sqrt{20}}=\frac{3}{2\sqrt{5}}=\frac{3\times \sqrt{5}}{2\sqrt{5}\times \sqrt{5}}=\frac{3\sqrt{5}}{10}$ …（答）

(4) $\sqrt{\frac{4}{5}}$ のように根号の中が分数になっているときは，次の公式を使って変形してから考えます．

${\sqrt{\frac{a}{b}}}=\frac{\sqrt{a}}{\sqrt{b}}$ （ただし $a,b\gt 0$ ）

$\sqrt{\frac{4}{5}}=\frac{\sqrt{4}}{\sqrt{5}}=\frac{2}{\sqrt{5}}=\frac{2\times \sqrt{5}}{\sqrt{5}\times \sqrt{5}}=\frac{2\sqrt{5}}{5}$

【例】…（これよりも下の解説は中学生には難しい･･･できなくてもよい．今，何をしてるのか確かめるために流し読みする程度）
(*1)　 $\frac{1}{\sqrt{3} + \sqrt{2}}$ (*2)　 $\frac{1}{5 - \sqrt{3}}$

　(*1)～(*2)の形の問題は，中学校の教科書では登場しません．これらは高校１年生で習うはずです．
　そもそも，１つの根号で書かれた $\sqrt{2}$ ， $\sqrt{3}$ のような数は２乗すれば整数や（整数の）分数になりますが，２つの根号の和で書かれた数は２乗しても整数や（整数の）分数にはなりません．

$(\sqrt{2})^2=2$ ←２乗は整数　○
$(\sqrt{3})^2=3$ ←２乗は整数　○
$(\sqrt{3}+ \sqrt{2})^2=3 + 2\sqrt{6} + 2=5 + 2\sqrt{6}$ ←２乗しても根号が残る　×
$(5 - \sqrt{3})^2=25 - 10\sqrt{3} + 3=28 - 10\sqrt{3}$ ←２乗しても根号が残る　×

だから，分母が根号の和や差（整数と根号の和や差も）になっているときは，「分母と同じ数」を掛けても根号ははずれません．このような場合には次の展開公式で $a$ も $b$ も２乗になることを利用します． $a^2,b^2$ だけが登場して $ab$ が登場しない公式はこれだけです．

$(a+ b)(a-b)=a^2-b^2$

(*1) 分母が根号の和になっていれば，根号の差を掛ける
$\frac{1}{\sqrt{3} + \sqrt{2}}=\frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2})(\sqrt{3} - \sqrt{2})}=\frac{\sqrt{3} - \sqrt{2}}{3-2}=\sqrt{3} - \sqrt{2}$

(*2) 分母が根号の差になっていれば，根号の和を掛ける
$\frac{1}{5 - \sqrt{3}}=\frac{5 + \sqrt{3}}{(5 - \sqrt{3})(5 + \sqrt{3})}=\frac{5 + \sqrt{3}}{25-3}=\frac{5 + \sqrt{3}}{22}$

(*) ３つ以上の和や差になっているときは，何回かに分けて行う
$\frac{1}{ \sqrt{2}+ \sqrt{3} - \sqrt{5}}=\frac{ (\sqrt{2}+ \sqrt{3}) + \sqrt{5} }{\lbrac (\sqrt{2}+\sqrt{3}) - \sqrt{5} \rbrac \lbrac (\sqrt{2}+ \sqrt{3}) + \sqrt{5} \rbrac }$
$=\frac{ (\sqrt{2}+ \sqrt{3}) + \sqrt{5} }{5 + 2\sqrt{6} -5}=\frac{ \sqrt{2}+ \sqrt{3} + \sqrt{5} }{2\sqrt{6}}$
$=\frac{ (\sqrt{2}+ \sqrt{3}) + \sqrt{5} }{5 + 2\sqrt{6} -5}=\frac{ (\sqrt{2}+ \sqrt{3} + \sqrt{5})\sqrt{6} }{12}}$
$=\frac{ 2\sqrt{3}+ 3\sqrt{2} + \sqrt{30} }{12}}$
（こんな問題を中学生向けに出すことはない）

(*) 分母に「整数や分数で表せない数」（高校ではこれを無理数という）がある場合でも，平方根で書ける数でなければ２乗しても整数や分数にはなりません．例えば，円周率 $\pi$ や高校で習う３乗根 $\sqrt[3]{2}$ （３乗したら２になる数字）などが含まれている場合には，この頁で扱った方法では分母を整数や分数に直すことはできません．

次の項目

次の各式を分母に根号のない形にしてください．和や差になっているものは，できるだけ簡単にしてください．

	問題	答	計算
(1)	$\frac{1}{\sqrt{3}}$	$\frac{\sqrt{3}}{3}$	[？]
(2)	$\frac{5}{\sqrt{2}}$	$\frac{5\sqrt{2}}{2}$	[？]
(3)	$\frac{3}{\sqrt{6}}$	$\frac{\sqrt{6}}{2}$	[？]

(4)	$\frac{7}{2\sqrt{3}}$	$\frac{7\sqrt{3}}{6}$	[？]
(5)	$\frac{5}{\sqrt{12}}$	$\frac{5\sqrt{3}}{6}$	[？]
(6)	$\frac{\sqrt{5}}{\sqrt{18}}$	$\frac{\sqrt{10}}{6}$	[？]

(7)	$\sqrt{\frac{3}{2}}$	$\frac{\sqrt{6}}{2}$	[？]
(8)	$\sqrt{\frac{15}{18}}$	$\frac{\sqrt{30}}{6}$	[？]
(9)	$6\sqrt{\frac{4}{54}}$	$\frac{2\sqrt{6}}{3}$	[？]

(10)	$\sqrt{3} + \frac{2}{\sqrt{3}}$	$\frac{5}{3}\sqrt{3}$	[？]
(11)	$\sqrt{18} + \frac{2}{\sqrt{50}}$	$\frac{16}{5}\sqrt{2}$	[？]
(12)	$\sqrt{\frac{1}{27}} - \sqrt{\frac{2}{{24}}$	$-\frac{\sqrt{3}}{18}$	[？]

次の項目

【問題】
　分母に根号のない形にしてください．
　はじめに左欄の問題を選び，続いて右欄の展開式を選んでください．やり直すときは，右欄を連打するのでなく，左欄の問題を選び直すことから始めてください．

$\frac{3}{\sqrt{2}}$ HELP

$\frac{\sqrt{3}}{\sqrt{2}}$ HELP

$\frac{2}{3\sqrt{2}}$ HELP

$\sqrt{\frac{2}{3}}$ HELP

$\frac{2}{\sqrt{27}}$ HELP

$\frac{3}{\sqrt{12}}$ HELP

$\frac{\sqrt{2}}{2}$ $\frac{3\sqrt{2}}{2}$ $\frac{\sqrt{2}}{3}$ $\frac{2\sqrt{2}}{3}$

$\frac{\sqrt{2}}{6}$ $\frac{\sqrt{2}}{9}$ $\frac{2\sqrt{2}}{9}$

$\frac{\sqrt{3}}{2}$ $\frac{3\sqrt{3}}{2}$ $\frac{\sqrt{3}}{3}$ 　 $\frac{2\sqrt{3}}{3}$

$\frac{\sqrt{3}}{6}$ $\frac{\sqrt{3}}{9}$ $\frac{2\sqrt{3}}{9}$

$\frac{\sqrt{6}}{2}$ $\frac{3\sqrt{6}}{2}$ $\frac{\sqrt{6}}{3}$ 　 $\frac{2\sqrt{6}}{3}$

$\frac{\sqrt{6}}{6}$ $\frac{\sqrt{6}}{9}$ $\frac{2\sqrt{6}}{9}$

次の項目

HELP
$\frac{\sqrt{2}}{3}+ \frac{1}{\sqrt{2}}$

HELP
$\sqrt{24}-\frac{6}{\sqrt{54}}$

HELP
$\sqrt{\frac{1}{12}}-\sqrt{\frac{1}{8}}+ \sqrt{\frac{1}{27}}$

HELP
$\sqrt{\frac{3}{32}}+ \sqrt{\frac{16}{24}} -\sqrt{\frac{5}{72}}$

HELP
$\sqrt{18}+ \frac{3}{\sqrt{12}}-\frac{4}{\sqrt{50}}$

$\frac{5\sqrt{2}}{3}$ $\frac{5\sqrt{2}}{6}$ $\frac{5\sqrt{3}}{3}$

$\frac{5\sqrt{3}}{6}$ $\frac{5\sqrt{6}}{3}$ $\frac{5\sqrt{6}}{6}$

$\frac{\sqrt{2}}{5}+ \frac{\sqrt{3}}{2}$ $\frac{3\sqrt{2}}{2}+ \frac{2\sqrt{3}}{3}$

$\frac{13\sqrt{2}}{5}+ \frac{\sqrt{3}}{2}$ $\frac{5\sqrt{3}}{6}- \frac{\sqrt{2}}{2}$

$\frac{11\sqrt{2}}{15}- \frac{\sqrt{3}}{2}$ $\frac{5\sqrt{3}}{18}- \frac{\sqrt{2}}{4}$

$\frac{11\sqrt{6}}{24}- \frac{\sqrt{10}}{12}$ $\frac{\sqrt{6}}{11}- \frac{\sqrt{10}}{12}$

*** END ***

(1)
$\frac{1}{\sqrt{3}}=\frac{1\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}=\frac{\sqrt{3}}{3}$

(2)
$\frac{5}{\sqrt{2}}=\frac{5\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}=\frac{5\sqrt{2}}{2}$

(3)
$\frac{3}{\sqrt{6}}=\frac{3\times \sqrt{6}}{\sqrt{6}\times \sqrt{6}}=\frac{3\sqrt{6}}{6}=\frac{\sqrt{6}}{2}$

［←戻る］

(4)
$\frac{7}{2\sqrt{3}}=\frac{7\times \sqrt{3}}{2\sqrt{3}\times \sqrt{3}}=\frac{7\sqrt{3}}{6}$

(5)

$\sqrt{12}=\sqrt{2^2\times 3}=2\sqrt{3}$ だから

$\frac{5}{\sqrt{12}}=\frac{5}{2\sqrt{3}}=\frac{5\times \sqrt{3}}{2\sqrt{3}\times \sqrt{3}}=\frac{5\sqrt{3}}{6}$

(6)

$\sqrt{18}=\sqrt{3^2\times 2}=3\sqrt{2}$ だから

$\frac{\sqrt{5}}{\sqrt{18}}=\frac{\sqrt{5}}{3\sqrt{2}}=\frac{\sqrt{5}\times \sqrt{2}}{3\sqrt{2}\times \sqrt{2}}=\frac{\sqrt{10}}{6}$

［←戻る］

(7)

$\sqrt{\frac{3}{2}}$ を変形するには，初めに，次の公式を使って２つの根号に分けます．

${\sqrt{\frac{a}{b}}}=\frac{\sqrt{a}}{\sqrt{b}}$ （ただし $a,b\gt 0$ ）

$\sqrt{\frac{3}{2}}=\frac{\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{3}\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}=\frac{\sqrt{6}}{2}$

(8)
$\sqrt{\frac{15}{18}}$
初めに，根号の中を約分して簡単にしておきます．
$\frac{15}{18}=\frac{5}{6}$
次に，分母と分子の２つの根号に分けます．

← ${\sqrt{\frac{a}{b}}}=\frac{\sqrt{a}}{\sqrt{b}}$

$\sqrt{\frac{5}{6}}=\frac{\sqrt{5}}{\sqrt{6}}$
$=\frac{\sqrt{5} \times \sqrt{6}}{\sqrt{6} \times \sqrt{6}}=\frac{\sqrt{30}}{6}$

(9)
$6\sqrt{\frac{4}{54}}$
初めに，根号の中を約分して簡単にしておきます．
$\frac{4}{54}=\frac{2}{27}$
次に，分母と分子の２つの根号に分けます．
$6\sqrt{\frac{2}{27}}=6\frac{\sqrt{2}}{\sqrt{27}}$
$=6\frac{\sqrt{2}}{3\sqrt{3}}=6\frac{\sqrt{2}\times \sqrt{3}}{3\sqrt{3} \times \sqrt{3}}=\frac{6\sqrt{6}}{9}=\frac{2\sqrt{6}}{3}$

［←戻る］

(10)
$\sqrt{3} + \frac{2}{\sqrt{3}}$

第２項を「分母に根号がない形」に直して
$x\sqrt{3} + y\sqrt{3}=(x + y)\sqrt{3}$
の形に持ち込む方向で変形していきます．

$\sqrt{3} + \frac{2}{\sqrt{3}}=\sqrt{3} + \frac{2\times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}$

← （上に掛けてある）ということは（横に掛けてある）というのと全く同じ

$=\sqrt{3} + \frac{2\sqrt{3}}{3}$
$=\sqrt{3} + \frac{2}{3}\sqrt{3}$
$=(1 + \frac{2}{3})\sqrt{3}$
$=\frac{5}{3}\sqrt{3}$

次のように分子に集めてもよい．
$\sqrt{3} + \frac{2\sqrt{3}}{3}=\frac{3\sqrt{3} + 2\sqrt{3}}{3}=\frac{5\sqrt{3}}{2}$

(11)
$\sqrt{18} + \frac{2}{\sqrt{50}}$
初めに，根号の中を簡単にしておきます．

$\sqrt{18}=\sqrt{3^2\times 2}=3\sqrt{2}$
$\sqrt{50}=\sqrt{5^2\times 2}=5\sqrt{2}$

$3\sqrt{2} + \frac{2}{5\sqrt{2}}$
次に，第２項を分母に根号のない形に直します．
$3\sqrt{2} + \frac{2\times \sqrt{2}}{5\sqrt{2}\times \sqrt{2}}=3\sqrt{2} + \frac{2\times \sqrt{2}}{10}$
$=3\sqrt{2} + \frac{\sqrt{2}}{5}=3\sqrt{2} + \frac{1}{5}\sqrt{2}=(3 + \frac{1}{5})\sqrt{2}$
$=\frac{16}{5}\sqrt{2}$
次のように分子に集めてもよい
$3\sqrt{2} + \frac{\sqrt{2}}{5}=\frac{15\sqrt{2} + \sqrt{2}}{5}=\frac{16\sqrt{2}}{5}$

(12)
$\sqrt{\frac{1}{27}} - \sqrt{\frac{2}{24}}$
第１項は，根号２つの分数に分けます．第２項は分数を約分しておきます．

$\sqrt{1}=1$ なので分子は１になります

$\frac{1}{\sqrt{27}} - \sqrt{\frac{1}{12}}$
さらに第２項を根号２つの分数に分けます．
$\frac{1}{\sqrt{27}} - \frac{1}{\sqrt{12}}$

以下の手順は，前の問題と同様です．
　ただし，分数が幾つもあるときの≪進め方≫は，次のように考えます．

▲「通分すると複雑になる」
◎「１つずつ分母を書き替える」

$\frac{1}{3\sqrt{3}} - \frac{1}{2\sqrt{3}}=\frac{1\times \sqrt{3}}{3\sqrt{3}\times \sqrt{3}} - \frac{1\times \sqrt{3}}{2\sqrt{3}\times \sqrt{3}}=\frac{\sqrt{3}}{9} - \frac{\sqrt{3}}{6}$
$=\frac{1}{9}\sqrt{3} - \frac{1}{6}\sqrt{3}=(\frac{1}{9} - \frac{1}{6})\sqrt{3}=(\frac{2}{18} - \frac{3}{18})\sqrt{3}$
$=- \frac{1}{18}\sqrt{3}$

次のように分子に集めてもよい
$\frac{\sqrt{3}}{9} - \frac{\sqrt{3}}{6}=\frac{2\sqrt{3}-3\sqrt{3}}{18}=-\frac{\sqrt{3}}{18}$
［←戻る］

(13)
$(2x + 1)(2x + 3)$

文字は $(2x)$
２数の和は $(1) + (3)=$ $4$
２数の積は $(1) \times (3)=$ $3$

$(2x + 1)(2x + 3)=$ $(2x)^2 +$ $4$ $(2x)+$ $3$
$=4x^2 + 8x + 3$

文字が $(2x)$ と考えるのが納得できない場合は， $2x=A$ とおいて
$(A + 1)(A + 3)$
を展開して
$A^2 + 4A + 3$
から，元の $x$ に戻すとよい
$(2x)^2 + 4(2x) + 3$
$=4x^2 + 8x + 3$

(14)
$(2x + \frac{1}{3})(2x - \frac{1}{4})$

文字は $(2x)$
２数の和は $(\frac{1}{3}) + (-\frac{1}{4})=(\frac{4}{12}) + (-\frac{3}{12})=$ $\frac{1}{12}$
２数の積は $(\frac{1}{3}) \times ( - \frac{1}{4})=$ $-\frac{1}{12}$

$(2x + \frac{1}{3})(2x - \frac{1}{4})=$ $(2x)^2 +$ $\frac{1}{12}$ $\times (2x)$ $-\frac{1}{12}$
$=4x^2 + \frac{x}{6} - \frac{1}{12}$

文字が $(2x)$ と考えるのが納得できない場合は， $2x=A$ とおいて
$(A + \frac{1}{3})(A - \frac{1}{4})$
を展開して
$A^2 + \frac{1}{12}A - \frac{1}{12}$
から，元の $x$ に戻すとよい
$(2x)^2 + \frac{1}{12}\times (2x) - \frac{1}{12}$
$=4x^2 + \frac{x}{6} - \frac{1}{12}$

(15)
$(3x - a)(3x + 4a)$

文字は $(3x)$
$a$ は数字と同じ係数と「みなす」
２数の和は $(-a) + (4a)=$ $3a$
２数の積は $(-a) \times (4a)=$ $-4a^2$

$(3x - a)(3x + 4a)=$ $(3x)^2 +$ $3a$ $\times (3x)$ $-4a^2$
$=9x^2 + 9ax - 4a^2$

文字が $(3x)$ と考えるのが納得できない場合は， $3x=A$ とおいて
$(A - a)(A + 4a)$
を展開して
$A^2 + 3aA - 4a^2$
から，元の $x$ に戻すとよい
$(3x)^2 + 3a\times (3x) - 4a^2$
$=9x^2 + 9ax - 4a^2$

［←戻る］