■ √の付いている式は,文字式と同じように,掛けたり展開したりできます.
例(a+b)2=a2+2ab+b2 と同様にして
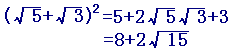 のように変形できます. のように変形できます.
【問題】
次の数を変形して,なるべく簡単にすると下のどの値になりますか.(√がない形にするか,または,√の中をなるべく簡単な整数にしなさい.)
[第1問 / 全10問]

次の問題を出す 途中経過を見る
=2 %2B \sqrt{2}) \( \displaystyle \sqrt{2}(\sqrt{2} +1)=2 +\sqrt{2} \) \( \displaystyle \sqrt{2}(\sqrt{2} +1)=2 +\sqrt{2} \)
=\sqrt{2}\sqrt{6} %2B \sqrt{2}\sqrt{3}=\sqrt{12} %2B \sqrt{6}) \( \displaystyle \sqrt{2}(\sqrt{6}+ \sqrt{3})=\sqrt{2}\sqrt{6} + \sqrt{2}\sqrt{3}=\sqrt{12} + \sqrt{6} \) \( \displaystyle \sqrt{2}(\sqrt{6}+ \sqrt{3})=\sqrt{2}\sqrt{6} + \sqrt{2}\sqrt{3}=\sqrt{12} + \sqrt{6} \)
 \( \displaystyle =\sqrt{2^2\times 3}+ \sqrt{6}=2\sqrt{3}+ \sqrt{6} \) \( \displaystyle =\sqrt{2^2\times 3}+ \sqrt{6}=2\sqrt{3}+ \sqrt{6} \)
^2=(\sqrt{2})^2 %2B 2\sqrt{2}\sqrt{3}%2B (\sqrt{3})^2) \( \displaystyle (\sqrt{2} + \sqrt{3})^2=(\sqrt{2})^2 + 2\sqrt{2}\sqrt{3}+ (\sqrt{3})^2 \) \( \displaystyle (\sqrt{2} + \sqrt{3})^2=(\sqrt{2})^2 + 2\sqrt{2}\sqrt{3}+ (\sqrt{3})^2 \)
 \( \displaystyle =2 + 2\sqrt{6} + 3=5 + 2\sqrt{6} \) \( \displaystyle =2 + 2\sqrt{6} + 3=5 + 2\sqrt{6} \)
^2=(\sqrt{5})^2 -2\sqrt{5}\sqrt{3}%2B (\sqrt{3})^2) \( \displaystyle (\sqrt{5} - \sqrt{3})^2=(\sqrt{5})^2 -2\sqrt{5}\sqrt{3}+ (\sqrt{3})^2 \) \( \displaystyle (\sqrt{5} - \sqrt{3})^2=(\sqrt{5})^2 -2\sqrt{5}\sqrt{3}+ (\sqrt{3})^2 \)
 \( \displaystyle =5 -2\sqrt{15}%2B 3=8-2\sqrt{15} \) \( \displaystyle =5 -2\sqrt{15}%2B 3=8-2\sqrt{15} \)
^2=2^2 - 2\times 2 \times \sqrt{3} %2B (\sqrt{3})^2) \( \displaystyle (2 - \sqrt{3})^2=2^2 - 2\times 2 \times \sqrt{3} + (\sqrt{3})^2 \) \( \displaystyle (2 - \sqrt{3})^2=2^2 - 2\times 2 \times \sqrt{3} + (\sqrt{3})^2 \)
 \( \displaystyle =4 - 4\sqrt{3} +3=7-4\sqrt{3} \) \( \displaystyle =4 - 4\sqrt{3} +3=7-4\sqrt{3} \)
^2=(\sqrt{3})^2 %2B 2\times \sqrt{3}\times 1%2B 1^2) \( \displaystyle (\sqrt{3} + 1)^2=(\sqrt{3})^2 + 2\times \sqrt{3}\times 1+ 1^2 \) \( \displaystyle (\sqrt{3} + 1)^2=(\sqrt{3})^2 + 2\times \sqrt{3}\times 1+ 1^2 \)
 \( \displaystyle =3 +2\sqrt{3} +1=4 +2\sqrt{3} \) \( \displaystyle =3 +2\sqrt{3} +1=4 +2\sqrt{3} \)
(\sqrt{5}%2B \sqrt{3})=(\sqrt{5})^2-(\sqrt{3})^2) \( \displaystyle (\sqrt{5}-\sqrt{3})(\sqrt{5}+ \sqrt{3})=(\sqrt{5})^2-(\sqrt{3})^2 \) \( \displaystyle (\sqrt{5}-\sqrt{3})(\sqrt{5}+ \sqrt{3})=(\sqrt{5})^2-(\sqrt{3})^2 \)
 \( \displaystyle =5-3=2 \) \( \displaystyle =5-3=2 \)
(2%2B \sqrt{3})=2^2-(\sqrt{3})^2) \( \displaystyle (2-\sqrt{3})(2+ \sqrt{3})=2^2-(\sqrt{3})^2 \) \( \displaystyle (2-\sqrt{3})(2+ \sqrt{3})=2^2-(\sqrt{3})^2 \)
 \( \displaystyle =4-3=1 \) \( \displaystyle =4-3=1 \)
(\sqrt{2}%2B 3)=2\sqrt{2}\times \sqrt{2}%2B 2\sqrt{2}\times 3%2B \sqrt{2}%2B 3) \( \displaystyle (2\sqrt{2}+ 1)(\sqrt{2}+ 3)=2\sqrt{2}\times \sqrt{2}+ 2\sqrt{2}\times 3+ \sqrt{2}+ 3 \) \( \displaystyle (2\sqrt{2}+ 1)(\sqrt{2}+ 3)=2\sqrt{2}\times \sqrt{2}+ 2\sqrt{2}\times 3+ \sqrt{2}+ 3 \)
 \( \displaystyle =4+ 6\sqrt{2}+ \sqrt{2}+ 3=7+ 7\sqrt{2} \) \( \displaystyle =4+ 6\sqrt{2}+ \sqrt{2}+ 3=7+ 7\sqrt{2} \)
(\sqrt{2}- \sqrt{3})) \( \displaystyle (\sqrt{2}+ 2\sqrt{3})(\sqrt{2}- \sqrt{3}) \) \( \displaystyle (\sqrt{2}+ 2\sqrt{3})(\sqrt{2}- \sqrt{3}) \)
^2 -\sqrt{2}\times \sqrt{3}%2B 2\sqrt{3}\times \sqrt{2}- 2\sqrt{3}\times \sqrt{3}) \( \displaystyle =(\sqrt{2})^2 -\sqrt{2}\times \sqrt{3}+ 2\sqrt{3}\times \sqrt{2}- 2\sqrt{3}\times \sqrt{3} \) \( \displaystyle =(\sqrt{2})^2 -\sqrt{2}\times \sqrt{3}+ 2\sqrt{3}\times \sqrt{2}- 2\sqrt{3}\times \sqrt{3} \)
 \( \displaystyle =2- \sqrt{6}+ 2\sqrt{6}-6=-4+ \sqrt{6} \) \( \displaystyle =2- \sqrt{6}+ 2\sqrt{6}-6=-4+ \sqrt{6} \)
→解説を隠す←
|
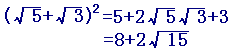 のように変形できます.
のように変形できます.


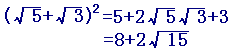 のように変形できます.
のように変形できます.

