|
■Excelを使った一元配置の分散分析,多重比較…例題・問題
○ この頁では,多くの学生のパソコン環境で利用しやすいと考えられるExcelを使った分散分析とフリーソフトRコマンダーを用いた分散分析+多重比較を扱う.
◇◇Excelによる◇◇
RとRコマンダーのインストール方法については【→この頁参照】
【1元配置の分散分析】(要約)1要因の分散分析ともいう
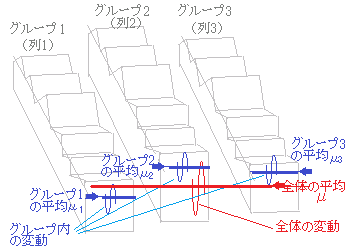
(1) 3つのグループから成るデータは一般に全体平均のまわりにバラついている.そのバラつきは,右図1にように各グループの平均値が違うことによるもの(グループ間の変動,列の効果)と,各グループの平均値からも各々のデータごとにずれているもの(グループ内の変動)に分けて考えることができる.
○ 2つの母集団の平均値に有意差があるかどうかはt検定で調べることができるが,3つ以上の母集団について平均値に有意差があるかどうかを調べには分散分析を使う.
○ 結果に影響を及ぼす様々な要因のうちで,他の要因は変えずに1つの要因の違いだけに着目して,その平均値に有意差があるかどうか調べるものを「一元配置法」(1因子の分散分析)という. すなわち,分散分析においては,全体の変動(各々の値と全体の平均との差の2乗の総和)をグループ内の変動(各々の値とそのグループの平均との差の2乗の和)とグループ間の変動に分けて,グループ間の分散とグループ内の分散の比がある比率よりも大きければ,この変動はグループ間の平均の差異によって生じたもの(列の効果)とみなす. (2) 右図1のような3つのグループの母集団平均に有意差があるかどうかを調べる分散分析においては,帰無仮説は
すべての平均が等しいこと:μ1=μ2=μ3
対立仮説は,その否定,すなわち
μ1≠μ2またはμ1≠μ3またはμ2≠μ3
とする.
上記のような帰無仮説,対立仮説の関係から,分散分析においては少なくとも1つのグループの母集団平均に他のグループの母集団平均と有意差があるか否かを判断する. (3) 例えば3つのグループについて2グループずつt検定を行うことと,3グループまとめて分散分析を行うこととは同じではない.すなわち,3つのグループについて2グループずつ有意水準5%のt検定を行うと,少なくとも1組に有意差が認められる確率は,3組とも有意差がないことの余事象だから
【例1】・・・対応のない一元配置
次の表1は異なる3つのグループA1,A2,A3について行った測定結果とする.これら3つのグループの母集団平均には有意差があるかどうか調べたい.
データはExcelワークシート上の左上端にあるものとする.(このデータを転記するには,上記のデータを画面上でドラッグ→右クリック→コピー→Excel上で左上端のセルに単純に貼り付けるとよい.ただし列見出し,行見出しの分が多いので削除する必要がある.) ■Excelでの操作方法 Excel2010, Exel2007での操作 ・データ→データ分析 Exel2002での操作 ・ツール→分析ツール →分散分析:一元配置→OK ・入力範囲:A1:C6(上記の桃色の欄も含める)(グループA2,A3には空欄がある[データ件数が異なる]のはかまわない.ただし,空欄に「欠席」,「余白」,スペース文字などの文字データがあると分散分析を適用できない.)
・データ方向:列 ・先頭行をラベルとして使用:上記のように入力範囲にラベルA1〜A3を含めた場合は,チェックを付ける ・α:有意水準を小数で指定する(デフォルトで0.05が入る) ・出力先:ブックやシートが幾つもできると複雑になるので,同じワークシートの右側の欄に出力するようにするには,[出力先]を選び空欄にE1などと書きこむ |
図1
※(参考)t検定と分散分析の関係
通常,2グループからなる1組の母集団平均の有意差検定はt検定で行い,3グループ以上あるときは分散分析で行うが,分散分析は2グループに対しても行うことができる.そのときは,両側検定となり(t値は得られないが)t検定と同じp値が得られる.(表1,表2参照) 2グループに対する分散分析において有意差が認められる場合は,以後の多重比較という問題はなくなり,当該2グループの平均に有意差があることになる. 表ア・・・表1のうちの1組(A1,A2)のデータに対するt検定の結果の出力
表イ・・・表アと同じ1組のデータに対する分散分析の結果の出力
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
→次のような出力結果が得られる. (ここに平均値の一覧表が入る) ↑
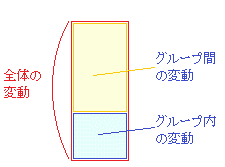
■Excelによる分散分析表の出力の見方 ○変動の下端行にある合計の欄 4.009 は,図1で赤で示した全体の変動,図2の全体の変動に対応している.
表1の12個のデータの全体の平均はm=10.01で,全体の変動は
○グループ内の変動 1.822 は,図1で青で示したもの,図2の青枠に対応している.
(9.5−m)2+(9.7−m)2+(10.1−m)2+··· ···+(10.2−m)2=4.009となる.
A1の5個のデータの平均はm1=9.68で,A1のグループ内の変動は
○グループ間の変動は「全体の変動」−「グループ内の変動」で求める.
(9.5−m1)2+(9.7−m1)2+(10.1−m1)2+···+(9.3−m1)2 A2の4個のデータの平均はm2=9.88で,A2のグループ内の変動は (10.1−m2)2+(10.5−m2)2+(9.6−m2)2+(9.3−m2)2 A3の3個のデータの平均はm3=10.73で,A3のグループ内の変動は (11.3−m3)2+(10.7−m3)2+(10.2−m3)2 これらの和,すなわちグループ内の変動は 1.822 となる.
4.009−1.822=2.187 となる.
○自由度は平均を使うたびに1つ減ると考えて(ある平均になるような元の変数の決め方からその確率を計算していくので,変数の個数から平均の分(1)だけ自由に決められる変数の数が減る)
※ (m1−m)2×5+(m2−m)2×4+(m3−m)2×3 としても同じ
グループが3個あるからグループ間の自由度は2
○変動を自由度で割ったものが分散の不偏推定値(不偏分散)
A1は標本数が5個ありその平均を使うから自由度は4,A2は標本数が4個ありその平均を使うから自由度は3,A3は標本数が3個ありその平均を使うから自由度は2.以上によりグループ内の自由度は4+3+2=9 合計で11
グループ間の変動÷グループ間の自由度=グループ間の分散 2.187÷2=1.094
○以上の結果,「観測された分散比」を「グループ間の分散」÷「グループ内の分散」によって求める
グループ内の変動÷グループ内の自由度=グループ内の分散 1.822÷9=0.202
1.094÷0.202=5.401
○F境界値は,分母の自由度=9,分子の自由度=2のときのF分布における5%点を読み取ったものであるが,コンピュータ処理においては自動的に計算される.
Excelワークシート関数を用いて =FINV(0.05, 分子自由度, 分母自由度) として計算したものと同じ
○P-値は,帰無仮説において上記のF比となる確率を求めたものであるが,コンピュータ処理においては自動的に計算される.
Excelワークシート関数を用いて =FDIST(求めた分散比, 分子自由度, 分母自由度) として計算したものと同じ
◎最終的に,「観測された分散比」が「F境界値より」も大きければ帰無仮説が棄却され,有意差が認められる.
5.401>4.256 だから有意差あり
(または,P-値が0.05よりも小さければ帰無仮説が棄却され,有意差が認められる.p=0.029<0.05だから有意差あり.通常, p<.05 と書く) |
■統計の参考書で一般に用いられる書き方1,書き方2
■用語・記号 ○変動, SS・・・平方和(sum of square)ともいう ○グループ・・・要因,条件,群,列,(水準)ともいう ○誤差, wc・・・グループ内,群内(within cell) ○自由度・・・dfとも書く(degree of freedom) ○分散, MS・・・平均平方(mean square)ともいう ○観測された分散比・・・F比,単にFとも書く ○P-値・・・p値,有意確率ともいう |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
【問題1】
次の表2は3つのグループからそれぞれ8人を選んで,ある運動能力を測定した結果とする.これら3つのグループにおいてこの運動能力の平均に有意差があるかどうかExcelの分析ツールを使って分散分析で示してください.
データを転記するには,画面上でドラッグ→反転表示→右クリック→コピーしてから,Excel上で貼り付けるとよい.
次の空欄を埋めてください.小数第4位を四捨五入して小数第3位まで答えてください. |
一元配置の分散分析で次のように出力されるので,0.018と答える.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
◇◇Rコマンダーによる◇◇
■多重比較
分散分析で有意差が認められた場合に,どの2グループ間の母集団平均に有意差があるのかの判断は,分散分析だけではわからない.具体的にどのグループ間に有意差があるのかを調べる方法は多重比較と呼ばれる.
○すべての組合せについてt検定を行うことと多重比較は異なる. ○分散分析(3個以上同時)と多重比較(2個ずつ)とは原理的に異なる処理が行われるので,分散分析で有意差があっても多重比較でおこなうと有意な組が1つもない場合,逆に分散分析では有意差がないのに多重比較を行うと有意な対があるような事が起こる.(「心理統計学の基礎」有斐閣アルマ/南風原朝和著 p.284) そこで通常は,分散分析において有意差があった場合だけ多重比較を行う(事後検定). ○Excelの組み込みの関数や分析ツールによって多重比較を行うことはできないので,ここではRコマンダーによって行う方法を述べる. フリーソフト:Rコマンダーで採用されている多重比較法はチューキー法である.(J.W.Tukey:アメリカの統計学者) |
※多重比較法には,チューキー法,シェッフェ法,LSD法,ライアン法など多くの方法があるが各々一長一短(有意差のないものでもあると判断し易い傾向のあるもの,逆に,有意差のないものをあると判断し易い傾向など)があることが知られており,参考書やソフトによって採用している方法が分かれている.(定説・多数説的なものが絞れない.) |
||||||||||||||||||||||||||||||||||||||||||
|
(1) Rコマンダーで一元配置(1要因の)分散分析・多重比較を行うためのデータの形
右の表3のような形のデータにおいてグループA1,A2,A3の母集団平均の有意差検定を行いたいとき,Rコマンダーで分散分析・多重比較を行うにはExcel上で表4のようなデータの形に直しておいてこれをRコマンダーから読み込むようにする.(グループ名は数値データではなく文字データとする.)
(2) Rコマンダーを起動するExcel2010, Excel2007での操作 (Excelの内部から)アドイン→RExcel→Start R Excel2002での操作 (Excelの内部から)RExcel→Start R →RExcel→RCommander:with separate menus (3) Excel上で右の表2に示した範囲をコピーする. (4) Rコマンダーのメニューから
データ→データのインポート:テキストファイルまたはクリップボード,URLから...
(5) 一元配置の分散分析を行い,同時に多重比較の結果も表示されるようにする→右図3のようにクリップボードを選択(3)でメモリに入れた内容をインポートする フィールドの区切り記号としてタブを選択 表2のように「列見出し」のないデータをコピーしているから「ファイル内に変数名あり」のチェックをはずす. (変数名がないので出力のときV1, V2という変数名が付けられる.) →OK (出力ウィンドウに Dataset <- read.table("clipboard", header=TRUE, sep="\t", na.strings="NA", + dec=".", strip.white=TRUE)などと表示される) (このとき,データがうまくインポートできているかどうかはRコマンダーのメニューで[データセットを表示]というボタンをクリックすると分かる)
(Rコマンダーのメニューから)統計量:平均:一元配置分散分析
(6) 出力ウィンドウに
→このとき右図4のように「2組ずつの平均の比較(多重比較)」にチェックを付ける→OK
> summary(AnovaModel.2)
Df Sum Sq Mean Sq F value Pr(>F)
V1 2 2.1870 1.09350 5.401 0.02877 *
Residuals 9 1.8222 0.20246
---
Signif.codes: 0 '***'0.001'**'0.01'*'0.05'.'0.1' '1
のように出力があり*が有意水準5%の有意差があること(* p<.05)を表している.同時に,右図5のようなグラフが別ウィンドウに表示される. 95%信頼区間が (-------・------) という形で表示されるがこのとき,それぞれ
A2 - A1 = 0
という仮説の信頼区間を表しているので,この信頼区間の中に0が含まれていなければその仮説は棄却されることになる.A3 - A1 = 0 A3 - A2 = 0 右図5ではA3−A1=0は信頼度95%の信頼区間に入っていないから帰無仮説が棄却され,これらの母集団平均には有意差があることがわかる. 以上により,3つのグループの母集団平均について分散分析を行うと有意水準5%で有意差が認められ,チューキー法による多重比較によりA1-A3の間に有意差があることがわかる. |

図3 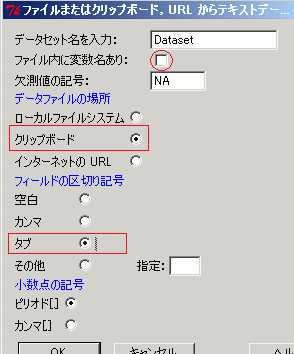 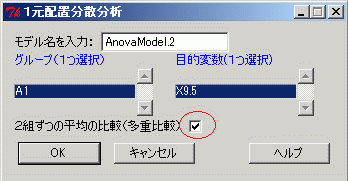 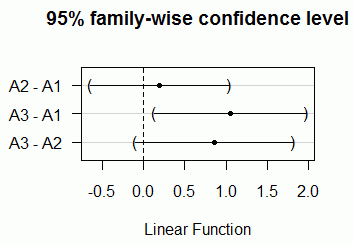 |
|
【問題2】
右の表5は上記の表2と同じデータをRコマンダーで使うためにデータの形を書き換えたものとする.これら3つのグループにおいてこの運動能力の平均に有意差があるかどうかRコマンダーを使って多重比較してください.
データを転記するには,画面上でドラッグ→反転表示→右クリック→コピーしてから,Excel上で貼り付けるとよい.
正しいものを番号で答えてください. 1 有意差のある組はない 2 有意差があるのはグループ1⇔2だけ 3 有意差があるのはグループ1⇔3だけ 4 有意差があるのはグループ2⇔3だけ 5 有意差があるのはグループ1⇔2, 1⇔3の2組 6 有意差があるのはグループ1⇔2, 2⇔3の2組 7 有意差があるのはグループ1⇔3, 2⇔3の2組 8 3組とも有意差がある
次のグラフが出力される.
 |
表5
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
【問題3】
右の表6は3学級の生徒の数学の得点とする.これら3つの学級について数学の平均得点に有意差があるかどうかRコマンダーを使って分散分析と多重比較をしてください.
データを転記するには,画面上でドラッグ→反転表示→右クリック→コピーしてから,Excel上で貼り付けるとよい.
p値は小数第4位を四捨五入して小数第3位まで,多重比較の結果は番号で答えてください. |
表6
はじめにExcel上でデータの形を上の表5のように作り変え,次にクリップボードからデータをインポートする.
一元配置の分散分析で多重比較にもチェックを付けておくと,次の表が出力される.
Df Sum Sq Mean Sq F value Pr(>F)
V1 2 709.48 354.74 5.0326 0.01586 *
Residuals 22 1550.76 70.49
(*が付いている)p=0.016<.05 だから有意差あり.
別ウィンドウに次のグラフが表示される.  |