|
■ 立体の体積(円柱,角柱,円錐,角錐の体積) [解説] 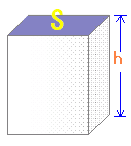
○【角柱,円柱の体積】 ■ 底面積が (底面積×高さ) 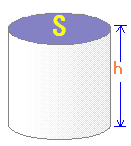
■ 特に円柱では,底面の半径をrとすると
※
なお,[重要]小学校の算数や中学高校の理科実験では近似値が好まれますが,中学高校の数学では,特に断り書きがなければ厳密な値で解答します.
中高の数学の答案で,例えば解答が |
|
■ 立体の体積(円柱,角柱,円錐,角錐の体積) [解説] 
○【角柱,円柱の体積】 ■ 底面積が (底面積×高さ) 
■ 特に円柱では,底面の半径をrとすると
※
なお,[重要]小学校の算数や中学高校の理科実験では近似値が好まれますが,中学高校の数学では,特に断り書きがなければ厳密な値で解答します.
中高の数学の答案で,例えば解答が |
|
|
  |
|
|
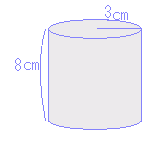  |
|
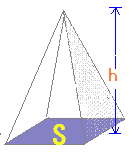
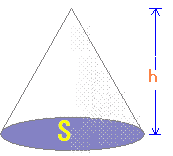
○【角錐,円錐の体積】 ■ 底面積が (底面積×高さ÷3)
なぜ,÷3になるのか?
⇒高校数学の積分を使えば証明できるが,小中学校でもこの公式は登場するので,結果を先取りして「柱の体積÷3」と覚えてしまう方が早い. |
  |
|
|
  |
|
|
  |
|
|
  |
|
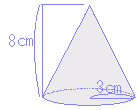
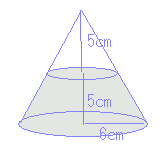
π×62×10÷3=120π(cm3) 上端の円錐の底面の半径(xとおく)は,比例(相似)の関係を使って求めることができる.縦:横x 5:x=10:6 → x=3(cm) 大きな円錐の体積から上端の円錐の体積 π×32×5÷3=15π(cm3) を引くとV=105π(cm3) |
  |
|
|
  |
|
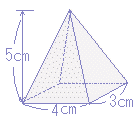
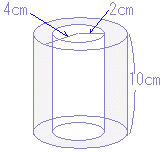
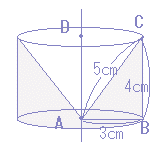
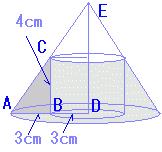
まず,比例(相似)の関係から AB:BC=AD:DE → 3:4=6:DE → DE=8 次に,円錐台の体積:π×6cm2×8÷3=96π(cm3)から上端の円錐の体積π×3cm2×4÷3=12π(cm3)を引いて84π(cm3) 中空の円柱の体積:π×32×4=36π(cm3) したがって,84π−36π=48π(cm3) |
  |
|
円錐の体積と表面積(高校入試問題)
【問題1】…(円錐の体積)
解説を見る
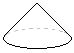 右の図のように,底面の半径が5cmで,高さが6cmの円すいがあります。この円すいの体積は何cm3ですか。ただし,円周率は
右の図のように,底面の半径が5cmで,高さが6cmの円すいがあります。この円すいの体積は何cm3ですか。ただし,円周率は(広島県2018年)
|
【問題2】…(円錐の展開図)
解説を見る
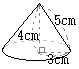 右の図のように,底面の半径が3cm,高さが4cm,母線の長さが5cmの円すい錐がある。
右の図のように,底面の半径が3cm,高さが4cm,母線の長さが5cmの円すい錐がある。次の(1),(2)に答えなさい。 (1) この円錐の体積を求めなさい。ただし,円周率は (2) この円錐の展開図を作図したとき,側面のおうぎ形の形として最も近いものを,次のア〜エの中から1つ選び,その記号をかきなさい。 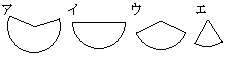 (和歌山県2018年)
(1)
【公式】
底面の半径が (2) 側面のおうぎ形の「弧の長さ」と底面の円の「円周の長さ」が一致する. おうぎ形の中心角を 180°よりも大きい(凹図形になる)→ア…(答) |
|
【問題3】…(体積比)
解説を見る
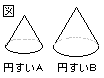 右の図の2つの円すいA,Bは相似で,その相似比は2:3です。円すいAの体積が40cm3のとき,円すいBの体積を求めなさい。
右の図の2つの円すいA,Bは相似で,その相似比は2:3です。円すいAの体積が40cm3のとき,円すいBの体積を求めなさい。
(滋賀県2017年)
ほとんどの受験生は,小学校の段階で次の公式を覚えていて,そのまま使うと思われる.
【公式】
相似比がm:nの2つの図形について 面積比は相似比の2乗比になる→m2:n2 体積比は相似比の3乗比になる→m3:n3
40:VB=23:33=8:27
8VB=40×27=1080 VB=135(cm3)…(答) |
【問題4】…(回転体の体積)
解説を見る
** 中3の三平方の定理を習ってから **
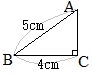 右の図の△ABCを,辺ACを軸として1回転してできる立体の体積を求めなさい。
右の図の△ABCを,辺ACを軸として1回転してできる立体の体積を求めなさい。ただし,円周率は (千葉県2015年)
|
|
【問題5】…(回転体の体積)
解説を見る
** 三平方の定理を使わずに解ける **
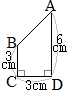 右の図の台形ABCDを,辺ADを軸として1回転してできる立体の体積を求めなさい。(円周率は
右の図の台形ABCDを,辺ADを軸として1回転してできる立体の体積を求めなさい。(円周率は(岐阜県2015年)
|
【問題6】…(回転体の体積)
解説を見る
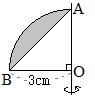 右の図のように,半径3cm,中心角90°のおうぎ形
右の図のように,半径3cm,中心角90°のおうぎ形(福井県2015年)
|
|
【問題7】…(球と円錐の体積)
解説を見る
 右の図のような半径9cmの半球があります。この半球と等しい体積の円すい錐について考えます。円錐の底面の半径が9cmであるとき,円錐の高さは何cmか求めなさい。
右の図のような半径9cmの半球があります。この半球と等しい体積の円すい錐について考えます。円錐の底面の半径が9cmであるとき,円錐の高さは何cmか求めなさい。
(滋賀県2015年)
|
【問題8】…(円錐の体積と表面積)
解説を見る
** 中3の三平方の定理を習ってから **
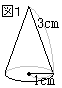 右の図1のように,底面の半径が1cm,母線の長さが3cmの円すいがある。
右の図1のように,底面の半径が1cm,母線の長さが3cmの円すいがある。このとき,次の問いに答えなさい。 ただし,円周率は (1) この円すいの体積を求めなさい。 (2) この円すいの表面積を求めなさい。 (富山県2016年)
(1) 円すいの高さ
円すいの体積は (2) 側面積を求めるためには,展開図のおうぎ形の中心角 底面の円周の長さは 側面のおうぎ形の弧の長さは これらが等しいから 底面積+側面積は |
|
■[個別の頁からの質問に対する回答][立体の体積について/17.3.29]
五角錐が、互角推に…
■[個別の頁からの質問に対する回答][立体の体積について/17.3.28]
=>[作者]:連絡ありがとう.あ〜間違いです.おもしろ漢字変換のネタにされそうなミスでした. ちょっとむずかしかったです
■[個別の頁からの質問に対する回答][立体の体積について/17.3.20]
=>[作者]:連絡ありがとう. 分かりやすいまとめでした❗
■[個別の頁からの質問に対する回答][立体の体積について/17.3.7]
=>[作者]:連絡ありがとう. 6年生の宿題が分からなくて困っていました。
そんな時にこのようなわかりやすいホームページがあったのでよかったです。とても感謝しています。
本当にありがとう…。
=>[作者]:連絡ありがとう. |