|
現在地と前後の項目 *** 楽しく学ぶ ***/今日は何日？/*** 方程式の基本 ***/等式の性質(解説)/解き方.検算(解説)/方程式.弱点克服/方程式.変形の仕方 /移項と割り算(問題)/方程式.解説と練習/問題1/問題2(タイマー付き)/問題3(カード合わせ)/問題4(カード合わせ)/問題5(∞)/ネズミに遊んでもらう/キツツキに遊んでもらう/カエルに遊んでもらう/セミに遊んでもらう/徹底練習/*** 分数の方程式 ***/小数,分数,かっこ/分数係数/分数形の方程式1/分数形の方程式2(答案付∞)/分数形の方程式3/*** 文章題 ***/式の練習 /方程式の文章題1 /方程式の文章題2 /方程式の文章題3/方程式の文章題4(答案付∞)/方程式の文章題（食塩水）/文章題（鶴亀算など）/*** 食塩水など ***/割合（百分率,歩合,分数）/食塩水の濃度1/食塩水の濃度2(答案付∞)/徹底練習.食塩水の濃度/*** 文字係数 ***/ａの値1/ａの値2/ ■方程式の解き方（弱点克服）
x−3=5やx+3=5のような方程式から解を求めるためには，次の「方程式の性質」を使って変形します．
【等式の性質１】
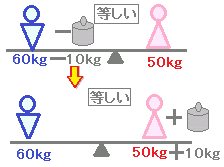
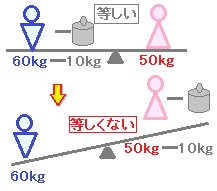
A=BならばA+C=B+C
２つの式AとBが等しいとき，両辺に同じ数Cを足した式も等しい．
［覚え方］⇒両辺に同じ数を足してもよい．
【例１】
x−3=5（もとの方程式：ここではx−3がA,5がB）  x−3+3=5+3（両辺に3を足した） x=5+3（左辺の−3が消えた） x=8（方程式の解） 「両辺に同じ数を足してもよい」という性質をそのまま使うと，上のように３段階の変形で方程式の解が得られますが，慣れてくればこの変形を「移項」という考え方を使って２段階でできます． （解説は右の欄）
|
◎【移項という考え方】
【例１】の途中の変形を見ると
○正しい移項の例x−3=5（もとの方程式） x−3+3=5+3（両辺に3を足した） x=5+3 （もとの方程式の−3を右辺に移動させる（移項する）と 符号が変わる） x=8（方程式の解）
⇒移項するときは符号を変えなければなりません．
「移項するもの」の符号だけを変えること．「足した結果」やそれ以外のものの符号は変えないことが重要．
|
||||||||
|
問題１次の方程式を「移項」という考え方で解くときに，正しい変形を選びなさい．（正解になれば次の変形が表示されます）
(1)x−4=7
|
(2)x−5=−8
|
||||||||
|
(3)x−6=10
|
(4)x−7=−13
|
|
【等式の性質２】
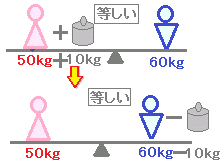
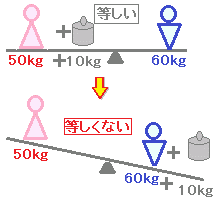
A=BならばA−C=B−C
２つの式AとBが等しいとき，両辺から同じ数Cを引いても等しい．
［覚え方］⇒両辺から同じ数を引いてもよい．
【例２】
x+3=5（もとの方程式：ここではx+3がA,5がB） x+3−3=5−3（両辺から3を引いた） x=5−3（左辺の+3が消えた） x=2（方程式の解） 「両辺から同じ数を引いてもよい」という性質をそのまま使うと，上のように３段階の変形で方程式の解が得られますが，慣れてくればこの変形を「移項」という考え方を使って２段階でできます． （解説は右の欄）
|
◎【移項という考え方】
【例２】の途中の変形を見ると
○正しい移項の例x+3=5（もとの方程式） x+3−3=5−3（両辺から3を引いた） x=5−3 （もとの方程式の+3を右辺に移動させる（移項する）と 符号が変わる） x=2（方程式の解）
⇒移項するときは符号を変えなければなりません．
「移項するもの」の符号だけを変えること．「足した結果」やそれ以外のものの符号は変えないことが重要．
|
||||||||
|
問題２次の方程式を「移項」という考え方で解くときに，正しい変形を選びなさい．
(1)x+8=2
|
(2)x+11=−4
|
||||||||
|
(3)x+1=9
|
(4)x+9=−6
|
|
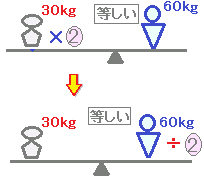
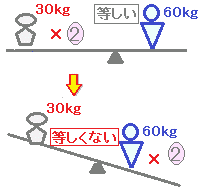
【等式の性質３】
A=BならばA×C=B×C
２つの式AとBが等しいとき，両辺に同じ数Cを掛けても等しい．
［覚え方］⇒両辺に同じ数を掛けてもよい．
【例３-２】
x÷2=3（もとの方程式：ここではx÷2がA,3がB） x÷2×2=3×2（両辺に2を掛けた） x=3×2（左辺の割り算の2が消えた） x=6（方程式の解）
【例３－２】
 x2=3（もとの方程式：ここではx2がA,3がB）x2×2=3×2（両辺に2を掛けた）x=3×2（左辺の分母の2が消えた） x=6（方程式の解） |
◎正しい計算の例
⇒左辺で割り算になっていた2（分母にあった2）は約分で消えて，右辺では掛け算として登場します．
この変形は「移項」とは関係がない．符号は変わらない．
|
||||||||
|
問題３次の方程式について，正しい変形を選びなさい．
(1)x÷3=12
|
(2)
x4=20
|
||||||||
|
(3)
x2=−6
|
(4)−
x3=6
|
|
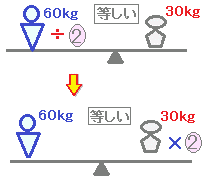
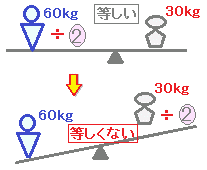
【等式の性質４】
A=Bならば
AC=BC（ただしC≠0）
２つの式AとBが等しいとき，両辺を同じ数Cで割ったものも等しい．
［覚え方］⇒両辺を同じ数で割ってもよい．
【例４】
2x=6（もとの方程式：ここでは2xがA,6がB） 2x2=62（両辺を2で割った）x= 62（左辺の2が約分で消えた）x=3（方程式の解） |
◎正しい計算の例
この変形は「移項」とは関係がない．符号は変わらない．両辺の符号が変わるのは「負の数で割る」という割り算の規則による場合です．
|
||||||||
|
問題４次の方程式について，正しい変形を選びなさい．
(1)3x=12
|
(2)2x=−10
|
||||||||
|
(3)−3x=5
|
(4)−5x=−8
|
|
【まとめの問題】
左右両辺に幾つもの式があるときは，次の手順で解きます．
ax=bの形になれば割り算をしたら答になります．
【例５】
2x−3=5（もとの方程式） 2x=5+3（定数項−3を右辺に移項した） 2x=8（←◎この形を目指す!!） x= 82（両辺を2で割った）
x=4（答）
【例６】
x+4=3x（もとの方程式） x−3x=−4（xの付いている項3xを左辺に移項し，定数項4を右辺に移項した） −2x=−4（←◎この形を目指す!!） x= −4−2（両辺を−2で割った）
x=2（答） |
【例７】
＃＃よくある間違いの例＃＃3x−5=−2x+10（もとの方程式） 3x+2x=10+5（xの付いている項−2xを左辺に移項し，定数項−5を右辺に移項した） 5x=15（←◎この形を目指す!!） x= 155（両辺を5で割った）
x=3（答）
xの付いている項はxを付けたまま移項することが重要
ax=bの形になるまではxとその係数は離れない．  |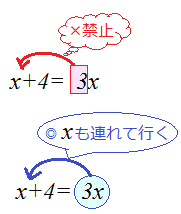
||
|
問題５次の方程式について，正しい変形を選びなさい．
(1)3x−2=16
|
(2)7x=5x+6
|
||
|
(3)5x+7=3x−1
|
(4)−4x+3=−x−12
|
||
|
(5)2x−3=−4x+5
|
(6)8−4x=−x+3
|