|
■母平均の推定・信頼区間(問題練習:正規分布を利用する場合) ○ 基本の復習
【中心極限定理】
○ 母集団が正規分布でないときでも,nが十分大きくなると標本平均の分布は, 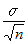 の正規分布 の正規分布○ 概ねn≧30のとき,標本平均の分布は正規分布とみなしてよい.
【母平均の信頼度95%の信頼区間】
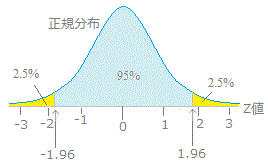
※この区間のことを,母平均μに対する信頼度95%の信頼区間という.nが十分大きいとき,母平均μが −1.96
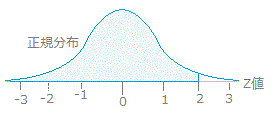
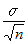 ≦μ≦+1.96 ≦μ≦+1.96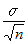 の区間にある確率は95%である. ※母平均の推定と信頼区間の問題については上の式のまま考えてもできるが,後に出てくるt検定,F検定などと統一的に理解するためには,上の式を 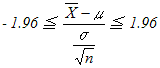 と変形して, と変形して,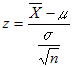 の値が-1.96と1.96の間になるかどうかで考えるとよい.(この値をz値ということがあり,z値の大小によって考えることにするのである.) の値が-1.96と1.96の間になるかどうかで考えるとよい.(この値をz値ということがあり,z値の大小によって考えることにするのである.)
【母標準偏差が未知のとき】
上の性質により,
nが十分大きいとき,母標準偏差σは標本標準偏差sに等しくなることが知られている. (微妙な話になるが避けて通れない話題) 母平均μが標本平均に等しいなどということではないし,母標準偏差σが標本平均の標準偏差 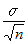 に等しいなどということでもない.nが十分大きいときに,等しいといえるのは母標準偏差σと標本標準偏差sだけ. に等しいなどということでもない.nが十分大きいときに,等しいといえるのは母標準偏差σと標本標準偏差sだけ.
概ねn≧30のとき,母標準偏差σが未知で標本標準偏差sが既知のとき,母平均の95%信頼区間を
−1.96
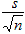 ≦μ≦+1.96 ≦μ≦+1.96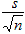 によって求めることができる. |
[記号の約束] 母集団の平均,標準偏差をギリシャ文字μ(ミュー),σ(シグマ)で表し,標本の平均,標準偏差を , sで表す. [おとぎ話による解説] 1人の母親の子供は多様であるが,子供の平均は母親の平均のまわりに集まる.(子供を見れば,親が分かる.) 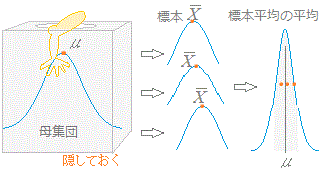
※ 標本平均の標準偏差として利用するもの
(*1)(*2) 母標準偏差σが既知のときはn≧30であると否にかかわらず,σを利用して計算すればよい. (*3) 母標準偏差が未知のとき,n≧30であれば標本の標準偏差sをσの代わりに用いる.母標準偏差が未知でn<30のときは正規分布ではなく後に習うt分布を利用する. |
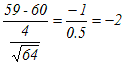
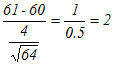
 ※ 正規分布表が手元になくてExcelで行うときは,
※ 正規分布表が手元になくてExcelで行うときは,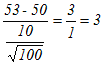
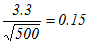
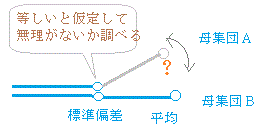 ある学校の中学3年生100人を無作為抽出して数学のテストについて調査したら平均72.5点であった.このテストについて全国の平均点は73.6点,標準偏差は5.8点であった.この中学校3年生の数学の学力は全国平均と比べて格差があるのだろうかという疑問を持ったとする.
ある学校の中学3年生100人を無作為抽出して数学のテストについて調査したら平均72.5点であった.このテストについて全国の平均点は73.6点,標準偏差は5.8点であった.この中学校3年生の数学の学力は全国平均と比べて格差があるのだろうかという疑問を持ったとする.