現在地と前後の項目

正の角・負の角/動径の表わす一般角/三角関数の定義 /(第2象限) /(第3象限) /(第4象限) /(まとめ)/弧度法の単位：ラジアン/三角関数の値(よく使う角度)/sin(π+θ)など/三角方程式　/三角不等式/三角関数のグラフ(sinθの平行移動)/(cosθの平行移動)/sin(θ－α)のグラフ（解説）/(振幅)/(周期)/(周期と振幅)/三角関数のグラフ(総合1)/三角関数のグラフ(総合2)/加法定理，倍角公式，３倍角公式，半角公式/加法定理の練習問題/２倍角公式.半角公式/加法定理の数値計算/積和.和積の公式/練習問題2/練習問題3/練習問題4/合成公式/三角不等式/三角関数（まとめ）/[センター]積和の公式/[センター]合成公式/三角関数公式一覧/三角関数公式プラス/三角形の証明・形状問題/センター試験.三角関数(2015年～)/
== 三角関数の値 ==(まとめ)
■解説
　ここまでに登場した三角関数の性質を要約すると，つぎの各式になる．(1)(2)は今までに登場していないが，右図から分かる．
(図を書けば分かるので，24個も公式を覚える必要はない．ただし，(8)だけは覚えた方がよい．)
　なお，.1tanθnnnn を cotθ と書く．

(1) 　　
　　 sin(360°×n+θ)=sinθ
　　cos(360°×n+θ)= cosθ
　　tan(360°×n+θ)= tanθ
(2)

　　 sin(90°−θ)=cosθ
　　cos(90°−θ)= sinθ
　　tan(90°−θ)= .1tanθnnnn = cotθ
(3)
　　 sin(90°+θ)=cosθ
　　cos(90°+θ)= − sinθ
　　tan(90°+θ)= − .1tanθnnnn = − cotθ
(4)
　　 sin(180°− θ)=sinθ
　　cos(180°− θ)= − cosθ
　　tan(180°− θ)= − tanθ
 (5)
　　 sin(180°+θ)= − sinθ
　　cos(180°+θ)= − cosθ
　　tan(180°+θ)= tanθ
(6)
　　 sin(270°−θ)= − cosθ
　　cos(270°− θ)= − sinθ
　　tan(270°− θ)= .1tanθnnnn = cotθ
(7)
　　 sin(270°+θ)= − cosθ
　　cos(270°+ θ)= sinθ
　　tan(270°+θ)= − .1tanθnnnn = − cotθ
(8)
　　sin( −θ)= − sinθ　（sinθは奇関数）
　　cos( − θ)= cosθ　（cosθは偶関数）
　　tan( − θ)= − tanθ　（tanθは奇関数）



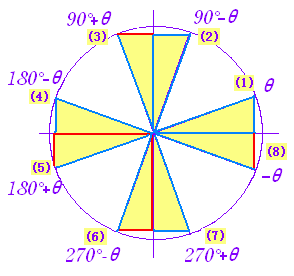(2)～(8)の比率と同じ比率になるものを(1)の図（角度がθの図）で探し，次に符号を考える．
(1) 　　
　　sin(360°×n+θ)=sinθ←/
　　cos(360°×n+θ)= cosθ←/
　　tan(360°×n+θ)= tanθ←/
(1)の場所で何周か回っても，縦横半径は同じになる
(2)
　　sin(90°−θ)=cosθ ←/
(2)の場所の sin は 縦／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．符号は全部正になるからcosθ
　　cos(90°−θ)= sinθ ←/
(2)の場所の cos は 横／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．符号は全部正になるからsinθ
　　tan(90°−θ)= .1tanθnnnn = cotθ ←/

(2)の場所の tan は 縦／横．これと同じ比率になるものを(1)の図（角度がθの図）で探す．縦横が反対になり符号は全部正になるからcotθ
(3)
　　 sin(90°+θ)=cosθ ←/
(3)の場所の sin は 縦／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．符号は全部正になるからcosθ
　　cos(90°+θ)= − sinθ ←/=−/
(3)の場所の cos は 横／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．１つ符号が変わるから−sinθ
　　tan(90°+θ)= − .1tanθnnnn = − cotθ←/ = −/

(3)の場所の tan は 縦／横．これと同じ比率になるものを(1)の図（角度がθの図）で探す．縦横が反対になり１つ符号が変わるから−cotθ
（再掲）
○半径だけは「つねに正」
▼〓縦(y)は上が正（青），下が負（赤）
▼〓横(x)は右が正（青），左が負（赤）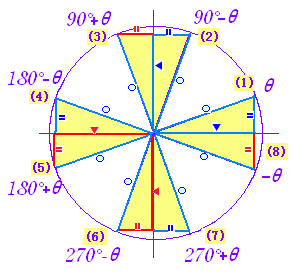
(4)
　　 sin(180°− θ)=sinθ ←/
(4)の場所の sin は 縦／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．符号は正になるからsinθ
　　cos(180°− θ)= − cosθ ←/ = −/
(4)の場所の cos は 横／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．１つ符号が変わるから−cosθ
　　tan(180°− θ)= − tanθ ←/ = −/
(4)の場所の tan は 縦／横．これと同じ比率になるものを(1)の図（角度がθの図）で探す．１つ符号が変わるから−tanθ

(5)
　　 sin(180°+θ)= − sinθ ←/ = −/
(5)の場所の sin は 縦／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．１つ符号が変わるから−sinθ
　　cos(180°+θ)= − cosθ ←/ = −/
(5)の場所の cos は 横／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．１つ符号が変わるから−cosθ
　　tan(180°+θ)= tanθ ←/ = /
(5)の場所の tan は 縦／横．これと同じ比率になるものを(1)の図（角度がθの図）で探す．２回符号が変わって元に戻るからtanθ
（再掲）
○半径だけは「つねに正」
▼〓縦(y)は上が正（青），下が負（赤）
▼〓横(x)は右が正（青），左が負（赤）
(6)
　　 sin(270°−θ)= − cosθ ←/ = −/
(6)の場所の sin は 縦／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．１つ符号が変わるから−cosθ
　　cos(270°− θ)= − sinθ ←/ = −/
(6)の場所の cos は 横／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．１つ符号が変わるから−sinθ
　　tan(270°− θ)= .1tanθnnnn = cotθ ←/ = /

(6)の場所の tan は 縦／横．これと同じ比率になるものを(1)の図（角度がθの図）で探す．縦横が反対になって符号が２回変わるからcotθ
(7)
　　 sin(270°+θ)= − cosθ ←/ = −/
(7)の場所の sin は 縦／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．１つ符号が変わるから−cosθ
　　cos(270°+ θ)= sinθ ←/
(7)の場所の cos は 横／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．符号は正だからsinθ
　　tan(270°+θ)= − .1tanθnnnn = − cotθ ←/ = − /

(7)の場所の tan は 縦／横．これと同じ比率になるものを(1)の図（角度がθの図）で探す．縦横が反対になって符号が１つ変わるから−cotθ
（再掲）
○半径だけは「つねに正」
▼〓縦(y)は上が正（青），下が負（赤）
▼〓横(x)は右が正（青），左が負（赤）
 (8)
　　sin( −θ)= − sinθ ←/ = −/
(8)の場所の sin は 縦／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．１つ符号が変わるから−sinθ
※f(−θ)=−f(θ)が成り立つ関数は奇関数と呼ばれる．sinθは奇関数
単に −がかっこの外に出るだけに見えるので，この公式を間違う生徒はめったにいない．

　　cos( − θ)= cosθ ←/
(8)の場所の cos は 横／半径．これと同じ比率になるものを(1)の図（角度がθの図）で探す．符号は正だからcosθ
※f(−θ)=f(θ)が成り立つ関数は偶関数と呼ばれる．cosθは偶関数
通常の展開式と同じように −がかっこの外に出るはずだと考えてしまう錯覚から，この公式を間違う生徒は多い！！．

≪要注意≫
　× → cos(−θ)= −cosθ
　○ → cos(−θ)= cosθ

　　tan( − θ)= − tanθ ←/ = −/
(8)の場所の tan は 縦／横．これと同じ比率になるものを(1)の図（角度がθの図）で探す．１つ符号が変わるから−tanθ
※f(−θ)=−f(θ)が成り立つ関数は奇関数と呼ばれる．tanθは奇関数
単に −がかっこの外に出るだけに見えるので，この公式を間違う生徒はめったにいない．


例題　次の式を簡単にしなさい．
(1)
sin(θ−180 °)+cos(90 °+θ)
sin(θ−180°)= − sin(180°− θ)= − sinθ
cos(90°+θ)= − sinθ だから
（原式）= − 2sinθ
(2)
sin(−θ)+sin(90°−θ)+sin(180°−θ)+sin(270°−θ)
（原式）= − sinθ+cosθ+sinθ−cosθ=0
(3)
tan(90°−θ)tan(180°+θ)
（原式）= cotθtanθ=1

■問題　次の式に等しいものを右の欄から選べ．
[ 第 1問 / 全8問中 ]
この問題の評価：　　次の問題を出す 		sinθ　　　　 − sinθ
cosθ　　　　 − cosθ
tanθ　　　　 − tanθ
cotθ　　　　 − cotθ
sin( -θ)

[ 第 1問 / 全5問中 ]
この問題の評価：　次の問題を出す　Help 		sinθ 　　− sinθ 　　2sinθ 　　− 2sinθ
cosθ 　　− cosθ 　　2cosθ 　　− 2cosθ
tanθ 　　− tanθ　　2tanθ 　　− 2tanθ
cotθ　　− cotθ 　　2cotθ 　　− 2cotθ
sinθ+cosθ　　　　 sinθ − cosθ
cosθ − sinθ　　　　 − sinθ − cosθ
0　　　 1　　　 − 1　　　 2　　　 − 2
sin(θ −270°)+cos(θ −180°)

（結果を確かめたいときの参考）
n×90°±θの三角関数をθの三角関数に直した結果の一覧表
ただし
.1tanθnnnn を cotθと書く．（コタンジェントθ）
.1sinθnnnn を cosecθと書く．（コセカントθ）
.1cosθnnnn を secθと書く．（セカントθ）
※見慣れない記号cotθ, cosecθ, secθが登場したら「３番目の文字の逆数」考えるとよい．
表A
θsinθcosθtanθ cotθsecθcosecθ
−θ−sinθcosθ−tanθ−cotθsecθ−cosecθ
90°−θcosθsinθcotθtanθcosecθsecθ
90°+θcosθ−sinθ−cotθ−tanθ−cosecθsecθ
180°−θsinθ−cosθ−tanθ−cotθ−secθcosecθ
180°+θ−sinθ−cosθtanθcotθ−secθ−cosecθ
270°−θ−cosθ−sinθcotθtanθ−cosecθ−secθ
270°+θ−cosθsinθ−cotθ−tanθcosecθ−secθ
360°−θ−sinθcosθ−tanθ−cotθsecθ−cosecθ
360°+θsinθcosθtanθ cotθsecθcosecθ
※赤道からスタートしたら三角関数は変わらない．北極，南極からスタートしたら三角関数が変わる．
表B
θsinθcosθtanθ cotθsecθcosecθ
θ−90°−cosθsinθ−cotθ−tanθcosecθ−secθ
θ−180°−sinθ−cosθtanθcotθ−secθ−cosecθ
θ−270°cosθ−sinθ−cotθ−tanθ−cosecθsecθ
θ−360°sinθcosθtanθcotθsecθcosecθ
表Aを先に考えて，次のルールで符号を付けると表Bになる．
sin(B−A)=−sin(A−B)：逆に引くと符号が変わる
cos(B−A)=cos(A−B)：逆に引いても符号は変わらない
tan(B−A)=−tan(A−B)：逆に引くと符号が変わる
cot(B−A)=−cot(A−B)：逆に引くと符号が変わる
sec(B−A)=sec(A−B)：逆に引いても符号は変わらない
cosec(B−A)=−cosec(A−B)：逆に引くと符号が変わる
※θ+90°, θ+180°, θ+270°などの三角関数は90°+θ, 180°+θ, 270°+θの三角関数に同じ
※１回転以上になる角，すなわちθ+450°, θ+540°, θ+630°,..., θ−450°, θ−540°, θ−630°,...などの三角関数はθ+90°, θ+180°, θ+270°,..., θ−90°, θ−180°, θ−270°,...の三角関数に同じ
メニューに戻る
■［個別の頁からの質問に対する回答］[三角関数の性質について／18.7.03］
問題2/5でcos(θ-270)をcos(270-θ)に変形させていますが-cos(270-θ)ではないでしょうか？ ご確認よろしくお願いします。
＝＞［作者］：連絡ありがとう．先頭の解説(8)にありますように，は偶関数，すなわちが成り立ちます．（とは異なり，になっても，符号は変化しません．間違いやすいものです）．
したがって，です．
■［個別の頁からの質問に対する回答］[三角関数の性質(まとめ)について／18.3.3］
cotとはなんですか？
＝＞［作者］：連絡ありがとう．一番最初に書いていますように，のことをで表します．だから，になります．
なお，というものはないのと同様に，というものはありません．のように角度があっての記号です．
■［個別の頁からの質問に対する回答］[三角関数の性質(まとめ)について／18.1.27］
数2三角関数 性質で問題３から 見たことのない計算式が出てきて ヒントもなし、どこを参考にしていいのか分かりません
＝＞［作者］：連絡ありがとう．解説がヒントです．見たこともない計算式とは，心外です．そのページの先頭から図あり式ありで解説している内容を踏まえて計算することになります．（あなたの読み方を見てみると［なぜわかるのかは，詳しく言えない］，問題３あたりまで余り読まずに進んでいます．時々，先頭部分まで振り返っていますが，それは一瞬で5回です．初めの方に重要な解説があるので，その部分を飛ばしてしまうと，理解できません．）
■［個別の頁からの質問に対する回答］[三角関数の性質(まとめ) について／16.12.19］
1/tanx＝cosx？
＝＞［作者］：連絡ありがとう．
（ア）基本公式そのものを質問しているものとして答えます．

が成り立ちますか？という質問だとします．結論から言えば，成り立ちません．
その頁の(6)にある

の右辺はコタンジェントです．

でお互いに分母と分子を入れ換えたもので，の方は授業では習う場合も習わない場合もあります．

（イ）これとは異なり，ある特定の角で1/tanx＝cosxが成り立つことはありますか？という質問である場合

となる場合は

になり，
となる角度では初めの式のが定義されませんので，結局この式が成り立つ角度はないということになります．
■［個別の頁からの質問に対する回答］[三角関数の性質(まとめ) について／16.12.4］
どこの教師よりも教科書よりも分かりやすかったです！ 三角関数(性質？)分からなかったので調べてたら このとんでもないわかりやすい図と説明が出てきて なんか泣きそうになりました笑 本当感激です！ これから頼らせて貰います！ 出会えて良かった、、、、、。！
＝＞［作者］：連絡ありがとう．

■このサイト内のGoogle検索■

△このページの先頭に戻る△
【 アンケート送信 】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．
○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）


質問に対する回答の中学版はこの頁，高校版はこの頁にあります