|
《例題1》 《解説》 グラフで見る P1から階段状に進んで行くと,数列は,
《例題2》 《解説》 グラフで見る 考え方は,例題1のときと同じです.x=2から出発して垂直→水平→垂直→水平→・・・と進みます. このとき,数列は,交点のx座標(y座標と考えても同じ)に収束します. 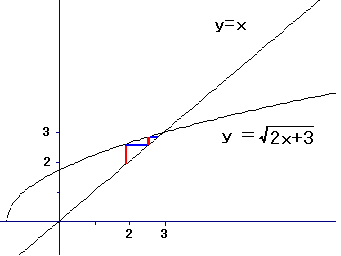 
■読み終わったら→ ここ ←をクリック■ |
|
《例題1》 《解説》 グラフで見る P1から階段状に進んで行くと,数列は,
《例題2》 《解説》 グラフで見る 考え方は,例題1のときと同じです.x=2から出発して垂直→水平→垂直→水平→・・・と進みます. このとき,数列は,交点のx座標(y座標と考えても同じ)に収束します.  
■読み終わったら→ ここ ←をクリック■ |
|
■[個別の頁からの質問に対する回答][はさみうち論法について/17.4.19]
例題の、実際の答案による解説のところで、辺々掛けた後の変形が分かりません。
他の項はどこに行ってしまったのですか?
=>[作者]:連絡ありがとう.中間項は両辺にあるので,約分と同様の仕組みで消えます. 初めの例では … … |