|
このページのバックアップ・ページ
《補集合》
(問題は下にあります.)
(グーグルブロガー版)は,こちら⇒ 《解説》 ■ 全体集合Uのうち,集合Aを取り除いた残りの部分をAの補集合といい 補集合
全体集合U={1,2,3,4,5,6,7,8,9},A={1,2,3,5,7}のとき <例2> Uは実数全体の集合,A={x|x>0}のとき, |
|
このページのバックアップ・ページ
《補集合》
(問題は下にあります.)
(グーグルブロガー版)は,こちら⇒ 《解説》 ■ 全体集合Uのうち,集合Aを取り除いた残りの部分をAの補集合といい 補集合
全体集合U={1,2,3,4,5,6,7,8,9},A={1,2,3,5,7}のとき <例2> Uは実数全体の集合,A={x|x>0}のとき, |
 
(3)
1, 2, 34, 5, 6 7, 8, 9 10
Aの外側とBの外側を合わせたものを考えます.→ 1,2,3,4,5,7,8,9,10
|
 
(4)
1, 2, 34, 5, 6 7, 8, 9 10
まずA
次に 最後にこれらを合わせると → 2,3,4,8,9,10 |
(5)
1, 2, 34, 5, 6 7, 8 |
|
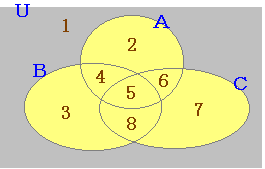
| 《問題2》 次の各式で表される集合は右図のどの部分を表すか.下の選択肢から選んで答えなさい.(1つクリックする) 解説 やり直す | 解説 やり直す |
| 解説 やり直す | 解説 やり直す |
| 《問題3》 次の各式で表される集合は右図のどの部分を表すか.下の選択肢から選んで答えなさい.(1つクリックする) 解説 やり直す | 解説 やり直す |
| 解説 やり直す | 解説 やり直す |
|
≪空集合≫ 〇 要素を1つも持たない集合を空集合(くうしゅうごう)といい,Øで表す. Ø={ }…(1)
任意の集合Aに対して,その要素の個数をn(A)で表す.この記号を使えば,
n(Ø)=0…(2)
〇 空集合は任意の集合Aの部分集合になっていると定める.Ø⊂A…(3)
集合Aに2つの要素a, bが属しているとき,Aの部分集合は
Ø, {a}, {b}, {a, b}
の4個ある.集合Aに3つの要素a, b, cが属しているとき,Aの部分集合は Ø, {a}, {b}, {c},
の8個ある.{a, b}, {a, c}, {b, c}, {a, b, c} 一般に,集合Aにn個の要素が属しているとき,Aの部分集合は2n個ある. 例えば,2つの要素a, bの場合,次の表のように各々「入る」か「入らない」か,2通りずつあり,全体で2×2通り=4通りになる.
|
(3)で述べたように,空集合は任意の集合の部分集合であると定めるから,
例えば,全体集合がU={a, b}でA={a}のとき,A={b}
このとき, Aの部分集合は,Øと{a} Aの部分集合は,Øと{b} このように,空集合はAにもAにも入っている. Ø⊂A
Ø⊂A
したがってA∩A=Ø
※おとぎ話による解説
全体集合Uが空集合でないとき,その1つの部分集合をAとすると,次の関係が成り立つ.
トリ軍団Aとケモノ軍団Aが争っているのに,コウモリ軍団Øは両方に入っている. ただし,コウモリ軍団には実体(要素)は1つもなく,実体がないから両方に入れる. 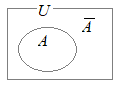 A⋃A=U…(4)
A⋃A=U…(4)A∩A=Ø…(5) A=A…(6) ∅=U…(7) U=∅…(8) |
|
《問題4》 全体集合Uは空集合でないものとし,その部分集合をA, B, C,空集合をØとするとき,次の各式の正誤を述べてください.下の選択肢から選んで答えなさい.(1つクリックする)
解説
やり直す
(3)により,空集合は任意の集合の部分集合であると定めているから,空集合自体の部分集合になる.
もっと一般的に,任意の集合は自分自身の部分集合になっている.A⊂A
したがって,「正」…(答) |
解説 やり直す |
| 解説 やり直す | 解説 やり直す |
| 解説 やり直す | 解説 やり直す |
| 解説 やり直す | 解説 やり直す |
|
■[個別の頁からの質問に対する回答][補集合について/18.4.27]
たびたび申し訳ありません。《問題3》の(4)の解説を拝見しても3行目の①②③④⑤⑦⑧となるには∩ではなく⋃ではないかと思われるのですがいかがでしょうか。
■[個別の頁からの質問に対する回答][補集合について/18.4.27]
=>[作者]:連絡ありがとう.問題を特定できました.確かにそうなりますが,∪が並んでいる問題はあまり良い問題にならず,当初作成したときの意図と変わってしまうので,暫定版を見てもらってから,書き換えるかもしれません. (4)の∩は⋃ではありませんか?
■[個別の頁からの質問に対する回答][補集合について/18.4.15]
=>[作者]:連絡ありがとう.(4)は問題1,2,3の3個あり,どの(4)か不明です. 問題または解説に∩のない問題2を外して,問題1または3としても,その指摘はあり得ないです. 問題も例題も最高でした。
■[個別の頁からの質問に対する回答][補集合について/17.9.28]
=>[作者]:連絡ありがとう. 例題が何問か出されていて良かった。
■[個別の頁からの質問に対する回答][補集合について/17.8.29]
=>[作者]:連絡ありがとう. 答えわかりません
■[個別の頁からの質問に対する回答][補集合について/17.5.18]
=>[作者]:連絡ありがとう.当面,お急ぎの場合は(携帯版には回答があります 例題が最高すぎる
■[個別の頁からの質問に対する回答][補集合について/17.4.23]
=>[作者]:連絡ありがとう.急には意味が分かりませんでしたが,ゆっくり考えて褒めてもらっていると解釈しました. とっても参考になりました。
これからもこのように問題形式になっているととても良いかと思います。後、もう少し問題を増やしたらいいと思います。
■[個別の頁からの質問に対する回答][補集合について/17.3.28]
=>[作者]:連絡ありがとう. わかりやすくて復習程度にでもためになりました
■[個別の頁からの質問に対する回答][補集合について/17.1.15]
=>[作者]:連絡ありがとう. 問題もあってわかりやすかった
■[個別の頁からの質問に対する回答][補集合について/16.11.22]
=>[作者]:連絡ありがとう. 例題つけるの素晴らしい!
=>[作者]:連絡ありがとう. |