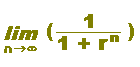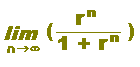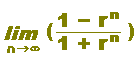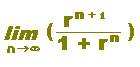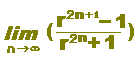|
ЃЎЃ@rn‚М‹ЙЊАЃF
Ѓi—v“_Ѓj
(1)−1<r<1Ѓ@‚М‚Ж‚«ЃC
ЃiЏШ–ѕЃjҐҐҐ•Є‚©‚и‚в‚·‚ўЏ‡‚Й‰рђа
Ѓin ЃЁ Ѓ‡‚М‚Ж‚«rn ЃЁ 0Ѓj‚Ж‚аЏ‘‚ (2)r=1Ѓ@‚М‚Ж‚«ЃC Ѓin ЃЁ Ѓ‡‚М‚Ж‚«rn ЃЁ 1Ѓj‚Ж‚аЏ‘‚ (3)r>1Ѓ@‚М‚Ж‚«ЃC Ѓin ЃЁ Ѓ‡‚М‚Ж‚«rn ЃЁ Ѓ‡Ѓj‚Ж‚аЏ‘‚ (4)rЃ…−1Ѓ@‚М‚Ж‚«ЃC Ѓin ЃЁ Ѓ‡‚М‚Ж‚«rn ‚НђU“® Ѓj‚Ж‚аЏ‘‚ (3)← Ѓ@‚’Ѓ„‚P‚М‚Ж‚«ЃC‚’ЃЃ‚PЃ{‚€Ѓ@Ѓi‚€Ѓ„‚OЃj‚Ж‚Ё‚‚Ж Ѓ@‚’‚ЋЃЃ(‚PЃ{‚€)‚ЋЃЃ‚PЃ{‚Ћ‚€Ѓ{(ђі‚Мђ”)Ѓ„‚PЃ{‚Ћ‚€ЃЁЃ‡ (2)← Ѓ@‚’ЃЃ‚P‚М‚Ж‚«ЃC–ѕ‚з‚©ЃD (1)← Ѓ|‚PЃѓ‚’Ѓѓ‚P‚М‚Ж‚«ЃC
Ѓ@‚µ‚Ѕ‚Є‚Б‚ДЃC‚’‚ЋЃЁ‚O
ЃбЃ‡Ѓ{Ѓ‡ЃCЃ‡Ѓ|Ѓ‡ЃCЃ‡Ѓ~Ѓ‡ЃCЃ‡ЃЂЃ‡‚МЊ`‚Й‚И‚й‚а‚МЃв
Ѓ›1Ѓ@Њ©‚©‚ЇЏгЃuЃ‡Ѓ{Ѓ‡Ѓv‚МЊ`‚Й‚И‚й‚а‚МЃ@ЃЛЃ@’ј‚ї‚ЙЃuЃ‡Ѓv‚Ж“љ‚¦‚з‚к‚й Ѓ›2Ѓ@Њ©‚©‚ЇЏгЃuЃ‡Ѓ~Ѓ‡Ѓv‚МЊ`‚Й‚И‚й‚а‚МЃ@ЃЛЃ@’ј‚ї‚ЙЃuЃ‡Ѓv‚Ж“љ‚¦‚з‚к‚й Ѓ›3Ѓ@Њ©‚©‚ЇЏгЃuЃ‡Ѓ|Ѓ‡Ѓv‚МЊ`‚Й‚И‚й‚а‚МЃ@ЃЛЃ@‚З‚ї‚з‚МЃ‡‚Є‹‚ў‚©‚МЊ€’…‚р‚В‚Ї‚й‚Ѕ‚Я‚ЙЃuЌЕ‘еЌЂ‚Е‚‚‚йЃv Ѓ›4Ѓ@Њ©‚©‚ЇЏгЃuЃ‡ЃЂЃ‡Ѓv‚МЊ`‚Й‚И‚й‚а‚МЃ@ЃЛЃ@‚З‚ї‚з‚МЃ‡‚Є‹‚ў‚©‚МЊ€’…‚р‚В‚Ї‚й‚Ѕ‚Я‚ЙЃu‚»‚к‚ј‚к‚рЌЕ‘еЌЂ‚Е‚‚‚йЃv Ѓ¦Ѓ›3ЃAЃ›4‚МЊ`‚М‹ЙЊА‚НЃiЋАЌЫ‚Й‚Н•s’и‚Й‚И‚й‚Ж‚НЊА‚з‚И‚ў‚ЄЃAЊ©‚©‚Ї‚МЊ`‚©‚зЃj•s’иЊ`‚М‹ЙЊА‚ЖЊД‚О‚к‚йЃB |