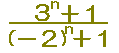rnの極限

← PC用は別頁

== ｒ^ｎの極限 == 《解説》
■　rnの極限： $\lim_{n\rightarrow \infty}r^n$ の値

（要点）

(1)−1<r<1　のとき， $\lim_{n\rightarrow \infty}r^n=0$

（n → ∞のときrn → 0）とも書く

(2)r=1　のとき， $\lim_{n\rightarrow \infty}r^n=1$

（n → ∞のときrn → 1）とも書く

(3)r>1　のとき， $\lim_{n\rightarrow \infty}r^n=\infty$

（n → ∞のときrn → ∞）とも書く

(4)r≦−1　のとき， $\lim_{n\rightarrow \infty}r^n$ は振動する

（n → ∞のときrn は振動）とも書く

（証明）･･･分かりやすい順に解説
(3)←
　ｒ＞１のとき，ｒ＝１＋ｈ　（ｈ＞０）とおくと
　ｒ^ｎ＝(１＋ｈ)^ｎ＝１＋ｎｈ＋(正の数)＞１＋ｎｈ→∞
(2)←
　ｒ＝１のとき，明らか．
(1)←
－１＜ｒ＜１のとき，

　０＜ｒ＜１のとき，

　ｒ＝１÷Ｒとおくと，Ｒ＞１だから(3)よりＲ^ｎ→∞

　したがって，ｒ^ｎ→０

　ｒ＝０のときｒ^ｎ→０は明らか
－１＜ｒ＜０のとき

｜ｒ｜^ｎ→０だからｒ^ｎ→０

(4)←

ｒ＝－１のとき，ｒ^ｎはnが偶数であるか，奇数であるかによって１，－１を振動するから，ｒ^ｎは振動
ｒ＜－１のとき，｜ｒ｜^ｎ→∞で符号はｎの偶数，奇数によって正負の値をとるから，振動

【例題１】
　一般項が次の式で与えられる数列の極限を求めなさい．
$3^n-2^n$

（解答）

○見かけ上 ∞−∞ の形になるものは，「最大項でくくる」と極限を求めやすい．
○最大項でくくると，次のように「どちらの∞が強いかの比較」ができる．

$3^n-2^n=3^n(1-(\frac{2}{3})^n)$
ここで， $3^n\rightarrow \infty$
$(\frac{2}{3})^n\rightarrow 0$ したがって $1-(\frac{2}{3})^n\rightarrow 1$
以上２つの積だから
$3^n-2^n=3^n(1-(\frac{2}{3})^n)\rightarrow \infty$

【例題２】
　一般項が次の式で与えられる数列の極限を求めなさい．
$\frac{2^n+ 1}{3^n-1}$

（解答）

○見かけ上 ∞÷∞ の形になるものは，分母と分子のそれぞれを「最大項でくくる」と極限を求めやすい．
○最大項でくくると，次のように「くくりだしたものの直接比較」ができる．

$\frac{2^n+ 1}{3^n-1}=\frac{2^n(1+ \frac{1}{2^n})}{3^n(1-\frac{1}{3^n})}=(\frac{2}{3})^n\times \frac{1+ \frac{1}{2^n}}{1-\frac{1}{3^n}}$
ここで
$(\frac{2}{3})^n\rightarrow 0$
また $1+ \frac{1}{2^n}\rightarrow 1\hspace{10},\hspace{10}1- \frac{1}{3^n}\rightarrow 1$ により
$\frac{1+ \frac{1}{2^n}}{1-\frac{1}{3^n}}\rightarrow 1$
以上２つの積だから
$(\frac{2}{3})^n\times \frac{1+ \frac{1}{2^n}}{1-\frac{1}{3^n}}\rightarrow 0$

《問題》　一般項が次の式で与えられる数列の極限を求めなさい．（初めはできなくても、「詳細」をよく見て「変形方法を脳裏に刻み込んで」おいて、２回目にできたらよい。）

≪１≫

≪２≫

≪３≫

≪４≫

≪５≫

≪６≫

≪７≫

≪まとめ≫

○1　見かけ上「∞＋∞」の形になるもの　⇒　直ちに「∞」と答えられる
○2　見かけ上「∞×∞」の形になるもの　⇒　直ちに「∞」と答えられる
○3　見かけ上「∞－∞」の形になるもの　⇒　どちらの∞が強いかの決着をつけるために「最大項でくくる」
○4　見かけ上「∞÷∞」の形になるもの　⇒　どちらの∞が強いかの決着をつけるために「それぞれを最大項でくくる」

※○3、○4の形の極限は（実際には不定になるとは限らないが、見かけの形から）不定形の極限と呼ばれる。

［注］直前にPC版から入られた場合は，自動転送でスマホ版に来ていますので，ブラウザの［戻るキー］では戻れません（堂々巡りになる）．下記のリンクを使ってメニューに戻ってください．

...（携帯版）メニューに戻る

...（PC版）メニューに戻る