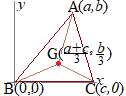
|
�@���̐}�̂Q�_�`(a,b),�a(c,d)�Ԃ̋����`�a�����߂�ɂ́C���p�O�p�`�����C�s�^�S���X�̒藝�i�O�����̒藝�j��p���ĎΕӂ����߂܂��D 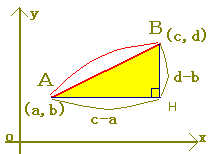 (����)�����|�� (�悱)�����|�� 
��ABH�ɂ��āC
���ɁC���_O(0,0)�Ɠ_A(a,b)�̊Ԃ̋�����
AB2=AH2+BH2 =(c−a)2+(d−b)2 ������ 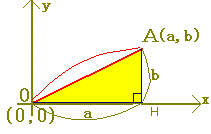 (����)���� (�悱)����
��OAH�ɂ��āC
OA =a2+b2 ������
�s�Q�_�Ԃ̋����̌����t
�Q�_A(a,b),B(c,d)�Ԃ̋�����
���Ȃ��C���̌����́C�ua=c�̂Ƃ��C���Ȃ킿AB���c�ɕ���ŎO�p�`�ɂȂ�Ȃ��Ƃ��v
��ub=d�̂Ƃ��C���Ȃ킿AB�����ɕ���ŎO�p�`�ɂȂ�Ȃ��Ƃ��v�ł����藧���܂��D ���ɁC���_O(0,0)�Ɠ_A(a,b)�̊Ԃ̋����� �y��z |

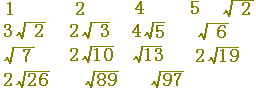
 �c��̒��_
�c��̒��_ �c��̒��_
�c��̒��_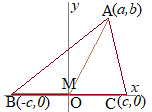
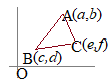 �R�_
�R�_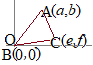 �}�`�S�̂s�ړ����Ă��C�}�`�̂Q�_�Ԃ̋����͕ω����Ȃ�����C�Ⴆ�Γ_
�}�`�S�̂s�ړ����Ă��C�}�`�̂Q�_�Ԃ̋����͕ω����Ȃ�����C�Ⴆ�Γ_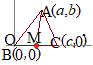 ����ɁC�}�`�S�̂���]�ړ����Ă��C�}�`�̂Q�_�Ԃ̋����͕ω����Ȃ�����C�Ⴆ�Γ_
����ɁC�}�`�S�̂���]�ړ����Ă��C�}�`�̂Q�_�Ԃ̋����͕ω����Ȃ�����C�Ⴆ�Γ_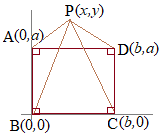
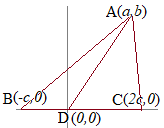 �E�}�̂悤��
�E�}�̂悤��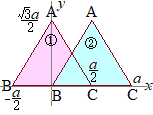 ���O�p�`
���O�p�`