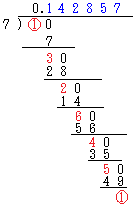
|
4. 循環節が長い分数のパターン
(1) フルに頑張るタイプ
⇒ 分母が で循環節の長さが で循環節の長さが 桁となるもの 桁となるもの
初めに例として示した, などがこれに当たります. などがこれに当たります.
分母が100以下の整数となる既約分数では,分母が次の値nのとき,循環節の長さがn-1桁になります.
これに該当しているのは素数ばかりですが,素数の全部がこれに該当するのでなく,11, 13, 31, 37, ...のように以下の(2)(3)...に登場するものもあります
7, 17, 19, 23, 29, 47, 59, 61, 97の9個
(2) 半分まで頑張るタイプ
⇒ 分母が で循環節の長さが で循環節の長さが 桁となるもの 桁となるもの

⇒1≦r≦12のうち6種類の余り1,10,9,12,3,4で一巡するので循環節の長さは6桁になります.

⇒1≦r≦30のうち15種類の余り1,10,7,8,18,25,2,20,14,16,5,19,4,9,28で一巡するので循環節の長さは15桁になります.
このタイプになる分母は,100以下では,他に次のものがあります.43,67,71,83,89を含めて計7個
(3) 3分の1まで頑張るタイプ
⇒ 分母が で循環節の長さが で循環節の長さが 桁となるもの 桁となるもの
このタイプになる分母は,100以下にはありませんが,1000までなら次のものがあります.
103, 127, 139, 331, 349, 421, 457, 463, 607, 661, 673, 691, 739, 829, 967
(4) 他の素数
4分の1まで頑張るタイプとして53, 173, 277, 317, 397, 769, 773, 797, 809, 853があります.
5分の1まで頑張るタイプとして11,251があります.
6分の1まで頑張るタイプとして79,547,643,751,907,997があります.
(5) 合成数でも(2)のタイプ以上に頑張るものがあります.
100以下の整数について,各々分母が で循環節の長さが で循環節の長さが の何パーセントかを示したもの. の何パーセントかを示したもの.
49=7×787.5%
14=2×753.84%
34=2×1751.51%
38=2×1951.35%
46=2×2351.11%
58=2×2950.87%
94=2×4750.53%
例えば

は,49=7×7であって,1から48までの48種類の余りの内で7,14,21,28,35,42の6種類の余りだけはなく,それ以外の余りで循環節の長さ42桁を実現しています.
また

は,14=2×7であって,1から13までの13種類の余りの内で1,3,5,7,9,11の奇数6種類の余りは登場せず,偶数2,4,6,8,10,12だけの余りで循環節の長さ6桁を実現しています.
(7分の1と比べると,循環節に登場する数字の並びは同じで前に巡回しない部分が増えたものになっています.)


5かけて10で割った等しいが,5を掛けると数字を回したものになるので,それを1桁下げたものになる.

以下同様に,つぎの分数も循環しない1桁が先頭に追加されるだけになる.




|
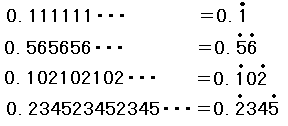
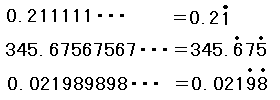
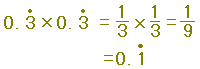 (最後のところで,分数を小数に直すには,割り算によります.)
(最後のところで,分数を小数に直すには,割り算によります.)
 右図に示すように,有理数(整数÷整数の分数)であるか無理数であるかの区別は,有限小数になるか無限小数になるかの区別には関係ありません.
右図に示すように,有理数(整数÷整数の分数)であるか無理数であるかの区別は,有限小数になるか無限小数になるかの区別には関係ありません.