対偶証明法と背理法

== 対偶証明法と背理法 ==
《解説》
**** １　対偶証明法 ****
○　ｐ，ｑ　あるいは　ｐ（ｘ），ｑ（ｘ）が条件であるとき，この条件が成り立つかどうかはｘの値しだいです．

【例】
　条件ｘ＞１をｐ（ｘ）で表わすとき，ｘ＝２ならばｐ（ｘ）は真ですが，ｘ＝０ならばｐ（ｘ）は偽です．

○　このように，条件については（どんなｘについても成り立つ［あるいは成り立たない］ような特別なものを除いて），それ自体の真偽を問うことはまれです－－条件は命題と異なり，真偽が定まるとは限りません．条件を満たすものの集合を考えるだけです．

【ここまでの要約】
　通常，x>1のような文字を含む条件に対しては，それ自体の真偽を問うことはまれで，その条件を満たすものの集合を考えます．
　すなわち，条件には集合を対応させます．

○　これに対して，「すべてのｘにたいして，ｐ（ｘ）が成り立つ」「あるｘについて，ｐ（ｘ）が成り立つ」という主張・判断は，正しいか間違っているかが定まる命題となります．一般に，条件ｐ（ｘ）に対して，「すべてのｘについて」あるいは「あるｘについて」という述語を付けたものは命題になります．

【例】
　すべてのｘについて，ｘ＞１　はｘ＝０，－１などで成立しないので偽の命題です．
【例】
　（文字を実数の範囲で考えるものとするとき）
　すべてのｘについて，ｘ^２＋１＞０　は真の命題です．（どんな実数ｘについても成立するからです．）
　あるｘについて，ｘ^２＋２ｘ＋２＜０　は偽の命題です．（この不等式には解がないからです．）

【ここまでの要約】
　通常，x>1のような文字を含む条件に対しては，それ自体の真偽を問うことはまれですが，

「すべてのxについてx2+1>0が成り立つ」
「あるxについてx2+2x+2<0が成り立つ」

などのように，条件に「すべての」「ある」を付けた主張は真偽の定まる命題になります．

○　ところで，一般に「ｐ（ｘ）→ｑ（ｘ）」は「すべてのｘについて，ｐ（ｘ）→ｑ（ｘ）」が省略されたものと決められています．
　そこで，ｐ（ｘ）→ｑ（ｘ）は命題です．

【ここまでの要約】

「すべてのxについて，p(x)ならばq(x)」

記号で書けば

「すべてのxについて，p(x)→q(x)」

は，単に

「p(x)→q(x)」

と省略的に書かれますので，これは真偽の定まる命題になります．すなわち「p(x)→q(x)」は「すべてのxについて，p(x)→q(x)」が省略されたものとなっているので命題です．

本当に，p(x)を満たすxがすべてq(x)を満たすのならばこの命題は真です．しかし，p(x)を満たすxの中に１つでもq(x)を満たさないものがあれば，この命題は偽になります．
【例】
「x>1→x>0」は真の命題です．
【例】
「x>0→x>1」は偽の命題です．（x=0.5のとき，x>0が成り立つのにx>1が成り立たないからです）

○　条件p(x)を満たすものの全体を集合Pで，条件q(x)を満たすもの全体を集合Qで表わすとき，命題「p(x)→q(x)」は，P⊂Qに対応します．

【ここまでの要約】
「p(x)→q(x)」を集合で考えると「P⊂Q」に対応する
すなわち

P⊂Qのときは「p(x)→q(x)」は真
P⊂Qでないときは「p(x)→q(x)」は偽

【例】

P={ x | x>1 }, Q= { x | x>0 }とするとき，
P⊂Qだから「x>1→x>0」は真
Q⊂Pでないから「x>0→x>1」は偽

■　対偶証明法
　ｐ→ｑが成り立つとき，すなわちＰ⊂Ｑのとき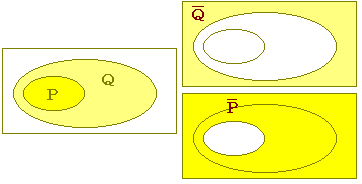，　です．

　逆に，が成り立つとき，すなわち　　のとき，P⊂Q　だから　ｐ→ｑ　です．
一般に，ｐ→ｑ　と　の真偽は一致します．
そこで，ｐ→ｑを証明したいときに，直接示すのが困難な場合，を示せばよいことになります．

＜対偶証明法＞
　を証明することにより，ｐ→ｑを間接的に証明する方法

■　対偶証明法の例

例１
　ｘ＋ｙ＋ｚ≧０のとき，ｘ．ｙ，ｚの少なくとも１つは０以上であることを証明しなさい．

（答案）

［考え方のポイント］
「少なくとも１つは０以上」の否定は，「全部０より小さい」

ｘ，ｙ，ｚ＜０　ならば　ｘ＋ｙ＋ｚ＜０　が成り立つ．
対偶が真であるから，もとの命題も真である．

例２
　ｎが自然数を表わすとき，ｎ^２が奇数ならば，ｎは奇数であることを証明しなさい．

（答案）
ｎ＝２ｋ（偶数）と仮定すると，ｎ^２＝４ｋ^２＝２(２ｋ^２）は偶数になる．
よって対偶により示された．

例３
　既約分数の分母・分子のどちらかは奇数であることを示しなさい。

(答案)

［考え方のポイント］
「少なくとも一方が奇数である」の否定=「両方とも偶数である」

既約分数において，ｍ，ｎともに偶数と仮定すると，分母・分子は２で約分できることになり，既約分数でなくなる。
よって，対偶により示された。　

例４
　ｍ，ｎを自然数とするとき，が既約分数であるならば，も既約分数であることを証明しなさい．

（答案）
ｍ，ｎが互いに素でないと仮定すると，ｍ＝ｋｍ’，ｎ＝ｋｎ’（ｋは２以上の整数）とおける．
このとき，＝　はｋで約分できる．
よって対偶により示された．

　我々の思考は，「個々の要素についての条件」から，「複合的な条件」の成否を判断する方が自然なので，
「複合的な条件」から「個々の要素についての条件」
を証明するような問題は，矢印を付け変えて（=対偶で考えて）
「個々の要素についての条件」の否定→「複合的な条件」の否定
を証明すると分かりやすくなります．

《問題》１　ｘ＋ｙ≧２ならばｘ，ｙのうち少なくとも１つは１以上であることを証明しなさい． (ア，イに入る語句を下の欄から選びなさい．) （答案）ｘ，ｙの［　ア　］ならば［　イ　］となる．よって対偶により示された．
［　ア　］両方とも１以下両方とも１より小さい少なくとも１つは１以下少なくとも１つは１より小さい	［　イ　］ｘ＋ｙ≧２ｘ＋ｙ＞２ｘ＋ｙ≦２ｘ＋ｙ＜２
HELP 「対偶によって示す」のだから，元の命題の対偶を作る．「ｘ＋ｙ≧２」の否定は「ｘ+ｙ＜２」，「ｘ，ｙのうち少なくとも１つは１以上である」の否定は「ｘ，ｙの両方とも１より小さい」次に，矢印の向きを付け変えると「ｘ，ｙの両方とも１より小さい」ならば「ｘ+ｙ＜２」になる．「ｘ＜1かつｙ＜1」ならば「ｘ+ｙ＜２」が成り立つから，これで対偶が示されたことになる．対偶証明法により，元の命題が示されたことになる．
２　整数ｍ，ｎについて，ｍｎが奇数ならば，ｍ，ｎはともに奇数であることを証明しなさい． (ア，イに入る語句を右欄から選びなさい．) （答案）ｍ，ｎの［　ア　］ならば［　イ　］となる．よって対偶により示された．
［　ア　］両方とも奇数両方とも偶数少なくとも一方が奇数少なくとも一方が偶数	［　イ　］ｍｎは奇数ｍｎは偶数
HELP 「対偶によって示す」のだから，元の命題の対偶を作る．「ｍｎは奇数」の否定は「ｍｎは偶数」，「ｍ，ｎはともに奇数」の否定は「ｍ，ｎの少なくとも一方は偶数」次に，矢印の向きを付け変えると「ｍ，ｎの少なくとも一方は偶数」ならば「ｍｎは偶数」になる．「ｍ，ｎの少なくとも一方は偶数」ならば「ｍｎは偶数」は正しいから，これで対偶が示されたことになる．対偶証明法により，元の命題が示されたことになる．
３　ｘ^２＋ｙ^２≦１ならばｘ≦１であることを証明しなさい．　(ア，イに入る語句を右欄から選びなさい．) （答案）ｙ^２≧０だから［　ア　］ならば［　イ　］となる．よって対偶により示された．
［　ア　］ｘ＞１ｘ＜１ｘ≧１ｘ≦１	［　イ　］ｘ^２＋ｙ^２＞１ｘ^２＋ｙ^２＜１ｘ^２＋ｙ^２≧１ｘ^２＋ｙ^２≦１
HELP 「対偶によって示す」のだから，元の命題の対偶を作る．「ｘ^２＋ｙ^２≦１」の否定は「ｘ^２＋ｙ^２＞１」，「ｘ≦１」の否定は「ｘ＞１」次に，矢印の向きを付け変えると「ｘ＞１」ならば「ｘ^２＋ｙ^２＞１」になる．「ｘ＞１」ならば「ｘ^２＞１，ｙ^２≧０したがってｘ^２＋ｙ^２＞１」が成り立つから，対偶が真となる．対偶証明法により，元の命題が示されたことになる．

**** ２　背理法 ****
■　背理法と対偶証明法は別のものです．背理法の一部に対偶証明法を用いることもありますが，そのような場合だけではありません．

■イラストによる背理法の説明(1)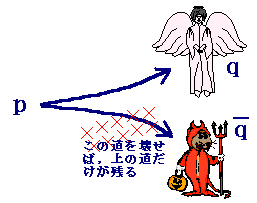

ｑとで世界の全部です． これ以外にはありません
Ｑ∪＝Ｕ（全体集合）

ｐ→ｑを証明したいが，ｑに行くのが困難なとき，
行きたくない方の道に進んでみて，そちらに進めば世界が破滅してしまう（矛盾がある）ことを言う．

（おとぎばなしによる解説）
地獄に行って，地獄を壊してしまうと天国だけが残ります・・・地獄に行かないと天国には行けません．

＃～地獄を見たものにしか，天国なんて分かるはずはないのだ，クソ－負けてたまるか～＃
と自分に言い聞かせると覚えやすい

ｐとを仮定して矛盾を示す．
（ｐも仮定します．）

ｐ

という形でｐとが矛盾という構造でもよい．(一部に対偶証明法を用いる)

ｐ　

→(数学的常識に反すること：1+1=1など)

という構造でもよい．

■イラストによる背理法の説明(2)

P⊂Qとは
P：卵の黄身が
Q：卵の白身の
中にあることだと思えばよい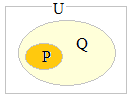

　論理的な関係p⇒q（pならばq）は，集合ではP⊂Qに対応します．
　言い換えれば，集合の関係としてP⊂Qとなっていることを示せば，p⇒qの証明になります．
　この証明は，集合P, Qの関係が一般のゆるい関係，すなわちP独自の部分，Q独自の部分，P, Qの共通部分から成り立っているのではなく，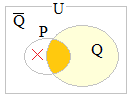

P∩Qが空集合になることを言えばよい．（右図の×印の部分が空集合になることを言う）．
　そうすると「P：卵の黄身」は「Q：卵の白身」の中にある部分だけから成り立っていることになり，P⊂Qが言える．
P∩Qが空集合になること（右図の×の部分には何もないこと）を示すには，「Pであって」かつ「Qである」ものが存在すると仮定すると，矛盾を生じることを示せばよい．
　何かある要素xが，x∈Pかつx∈Qを満たすとすると具合の悪いことが起こることを示せばよい．

＜背理法＞
ｐとを仮定して矛盾を示す方法
※ｐを仮定することが重要．この点が対偶証明法と異なり，結論として

が導ける場合に限られず，他の内容でも数学的に矛盾することが示せたら何でもよいので，自由度が大きい．

■　背理法の例

例１
　自然数ａ，ｂ，ｃについて，ａ^２＋ｂ^２＝ｃ^２が成り立つとき，ａ，ｂ，ｃのうち少なくとも１つは偶数であることを証明しなさい．

（答案）
ａ^２＋ｂ^２＝ｃ^２・・・(1)
ａ，ｂ，ｃは奇数・・・(2)　と仮定する．
(2)よりａ^２＋ｂ^２は奇数＋奇数で偶数となり，ｃ^２は奇数・・・(3)
(3)は(1)と矛盾する．
ゆえに，ａ，ｂ，ｃのうち少なくとも１つは偶数である．

例２
　が無理数であることを用いて，が無理数であることを証明しなさい．

(答案)

＝

（ｍ，ｎは整数）と仮定する．
両辺を２乗すると２＋３＋２＝（）^２

＝

となるが，左辺は無理数，右辺は有理数なので矛盾．
ゆえに，は無理数

例３
　△ＡＢＣにおいて，
ａ＜ｂならば∠Ａ＜∠Ｂ・・・(1)
ａ＝ｂならば∠Ａ＝∠Ｂ・・・(2)
ａ＞ｂならば∠Ａ＞∠Ｂ・・・(3)
が成り立つ．これらを用いて，(1)(2)(3)の逆が成り立つことを証明しなさい．

（答案）
∠Ａ＜∠Ｂのとき，
ａ＝ｂと仮定すると(2)により∠Ａ＝∠Ｂ　これは∠Ａ＜∠Ｂと矛盾する．
ａ＞ｂと仮定すると(3)により∠Ａ＞∠Ｂ　これは∠Ａ＜∠Ｂと矛盾する．
以上により，∠Ａ＜∠Ｂならばａ＜ｂ

(2)(3)の逆も同様にして示される． 背理法の一種の「転換法」と呼ばれる方法です．転換法は(1)(2)・・・の仮定側がすべての場合を尽くしていて，(1)(2)・・・の結論側に共通部分がなければいつでも使えます．

例４
　素数は無限個あることを証明しなさい．

（答案）
素数は有限個だけあると仮定し，これらをp₁,p₂,p₃,p₄,...，ｐ_ｎとおく
p₁・p₂・p₃・p₄･･･ｐ_ｎ＋１はp₁,p₂,p₃,p₄,...，ｐ_ｎのいずれでも割り切れない（１余る）から素数である．
これは矛盾であるから，素数は無限個ある．（ユークリッドの証明）

例５
　は無理数であることを証明しなさい．

（答案）
　

が有理数であると仮定し，これをとおく.　（ここに，ｍ，ｎは整数で互いに素）

(*)のようなことが起こるのは，ｎが２の倍数でｍも２の倍数の場合に限るということが示される．

とすれば，約分できるはずになる．結局，そんな既約分数は存在しえないことになる．

両辺を２乗すると $2=\frac{n^2}{m^2}$ …(*)
２ｍ^２＝ｎ^２
よって，ｎは２の倍数・・・(1)
ｎ＝２ｋとおく
２ｍ^２＝４ｋ^２
ｍ^２＝２ｋ^２
よって，ｍは２の倍数・・・(2)
(1)(2)はｍ，ｎが互いに素という仮定に反し，矛盾．
ゆえに，は無理数

　※この証明を見て，「ｍ，ｎは整数で互いに素」などという根本的には重要でなさそうな仮定と矛盾するということによって証明を行っていることについて，普通の感覚の高校生なら，なんとなく割り切れない印象を持つかもしれない．
　しかし，この証明は昔から有名な証明で，高校生としては，まず「そんな形の矛盾でもよいのか～♪」と感心して，次に「これに味をしめて」「機会があったら真似しよう」と考えるとよい
⇒ころんでもタダでは起きないしたたかさが重要

《問題》１　２１人を４組に分けたとき，どの組かは必ず６人以上になることを証明しなさい． (ア，イ，ウに入る語句を下欄から選びなさい．) （答案）２１人を４組に分けたとする・・・(1) どの組も［　ア　］以下で４組あると仮定する・・・(2) (2)より合計［　イ　］以下となる．・・・(3) (3)は(1)と矛盾するから，［　ウ　］
［　ア　］４人　５人　６人	［　イ　］２０人　２１人２４人　２５人	［　ウ　］全部で３組以下全部で５組以上どこかの組は５人以上すべての組は５人以上どこかの組は６人以上すべての組は６人以上
２　自然数ａ，ｂ，ｃについて，ａ^２＋ｂ^２＝ｃ^２が成り立つとき，ａ，ｂ，ｃのうち少なくとも１つは３の倍数であることを証明しなさい． (ア，イ，ウに入る語句を下欄から選びなさい．) （答案）ａ，ｂ，ｃのいずれも［　ア　］と仮定する．・・・(1) ところで　（３ｋ）^２＝３（３ｋ^２）　（３ｋ＋１）^２＝３（３ｋ^２＋２ｋ）＋１　（３ｋ＋２）^２＝３（３ｋ^２＋４ｋ＋１）＋１だから，(1)のとき　　ｃ^２は［　イ　］　　ａ^２＋ｂ^２は［　ウ　］これらが等しいことは矛盾であるから，ａ，ｂ，ｃのうち少なくとも１つは３の倍数である．
［　ア　］３の倍数である３の倍数でない	［　イ　］３で割ると１余る３で割ると２余る	［　ウ　］３の倍数である３で割ると１余る３で割ると２余る
３　√3が無理数であることを用いて，２＋√3が無理数であることを証明しなさい． (ア，イ，ウに入る語句を下欄から選びなさい．) （答案）２＋√3が［　ア　］であると仮定する．・・・(1) ２＋√3＝ｒ　（ｒは［　ア　］）とおくと √3＝ｒ－２となる．・・・(2) (2)の左辺は［　イ　］，右辺は［　ウ　］これは矛盾であるから，２＋√3は無理数である．
［　ア　］有理数無理数	［　イ　］有理数無理数	［　ウ　］有理数無理数
４　点Ｃを中心とする半径Ｒの円と直線Ｌがあって，点ＣからＬにひいた垂線の長さをｄとするとき，ｄ＜ＲならばＬは円と２点で交わる・・・(1) ｄ＝ＲならばＬは円と１点で接する・・・(2) ｄ＞ＲならばＬは円と共有点を持たない・・・(3) 　これらを用いて，(1)(2)(3)の逆をそれぞれ証明しなさい． (ア，イ，ウに入る語句を下欄から選びなさい．) （答案） *Ｌは円と２点で交わるとき，・・・() ｄ＝ＲならばＬは円と［　ア　］．これは()と矛盾する．* *ｄ＞ＲならばＬは円と［　イ　］．これは()と矛盾する．ゆえに，Ｌが円と２点で交わるとき，［　ウ　］． (2)(3)の逆も同様にして示される．**
［　ア　］２点で交わる１点で接する共有点を持たない	［　イ　］２点で交わる１点で接する共有点を持たない	［　ウ　］ｄ＜Ｒｄ＝Ｒｄ＞Ｒ
５　ｎが２以上の整数であるとき，は無理数となることを証明しなさい． (ア，イ，ウに入る語句を下欄から選びなさい．) （答案）　ｎ＜＜ｎ＋１だから，は［　ア　］ではない．・・・(1) 　が［　イ　］であると仮定すると，・・・(2) (1)(2)より　＝とおくと　（ｐ，ｑは正の整数で互いに素，ｐ≠１）・・・(3) 左辺は［　ウ　］で，右辺は(3)により［　ウ　］でない．これは矛盾であるから，は無理数
［　ア　］整数有理数無理数	［　イ　］整数有理数無理数	［　ウ　］整数有理数無理数

(携帯版)...メニューに戻る

...（PC版）メニューに戻る

■［個別の頁からの質問に対する回答］[対偶証明法と背理法について／18.6.25］

お世話になります。背理法を使って数について考えていますが、行き詰まってしまいました。知恵をお借りできませんでしょうか？任意の有理数をY、任意の無理数をMとする。Y÷Mが有理数なのか無理数なのか、両方ありえるのか考える。 Y÷M=Y/Mであり、これが有理数だと仮定すると、互いに素な自然数a.bを用いてa/bと表せるので、 (Y/M)=(a/b) 両辺にMaをかけると、Yb=Maとなり、左辺は有理数、右辺は無理数なので矛盾する。したがって、Y÷M=有理数という仮定は誤りで、Y÷M=無理数となる。ところで、Y=0のとき、Y÷M=0となり、有理数となってしまう。と、こんな具合に無理数なのか、有理数なのかわかりません。私の解き方、どこがおかしいのかわかりませんか？よろしくお願いいたします。
＝＞［作者］：連絡ありがとう．
「両辺にMaをかけると、Yb=Maとなり」の部分はおかしいですが，ほぼ合っています．ただし，主張の内容をはっきりしなければなりません．
ア） $Y\ne0$ のとき
$\frac{Y}{M}=\frac{a}{b}$
の両辺に $\frac{Mb}{a}$ を掛けると
$\frac{Ya}{b}=M$
左辺は有理数で右辺は無理数だから矛盾．よって元の式は無理数．
イ） $Y=0$ のとき
$\frac{Y}{M}=0$
は有理数.
したがって，有理数になる場合と無理数になる場合がある．
問題が，「任意の有理数をY、任意の無理数をMとするとき，Y÷Mは無理数になる」という命題ならば，イ）が反例となって偽
問題が，「任意の有理数をY、任意の無理数をMとするとき，Y÷Mは有理数になる」という命題ならば，ア）により偽

■［個別の頁からの質問に対する回答］[対偶証明法と背理法について／18.6.23］

証明問題では、背理法とか対偶法といった証明のテクニックだけでは点がとれません。例えば無理数は整数/整数で表せないとか、無理数÷有理数は無理数みたいな、予備知識が必要です。そこで、大学入試の証明問題に必要でよく問われる予備知識をまとめたノートを作り始めたのですが、なかなか必要な予備知識をまとめたサイトが見当たりません。ゲイシャ様のページでそれら予備知識をまとめたページがあるとうれしいです。
＝＞［作者］：連絡ありがとう．「幾つか」は可能ですが「全部」は無理でしょう．

■［個別の頁からの質問に対する回答］[対偶証明法と背理法について／16.11.26］

1対偶証明法の問題1で［ア］の選択肢両方とも1より小さい、少なくとも１つは1以下、少なくとも１つは1より小さいの３つを選んでもエラーになり、404:File Not Found となって結果が表示されません。ゲイシャさんの管理者に問い合わせるようにとのことでしたので、ここに書かせていただきました。僕はiPadでSafariを使ってこのページを開いています。(使っている検索エンジンはGoogleです。)肝心な正解の選択肢でさえ開けませんので(とはいえとても難しい問題というわけではありませんが、、、)どうかご点検をお願いいたします。補足:なぜか唯一両方とも1以下の選択肢だけは反応してバツになります。[イ]の方は問題ありませんでした。
＝＞［作者］：連絡ありがとう．「あ〝～」ビックリ仰天のプログラムミスでしたので，訂正しました．

■［個別の頁からの質問に対する回答］[対偶証明法と背理法について／16.8.23］

背理法例５について。なぜ、n/mが互いに素という仮定をつけていいのかがよく分からないのですが、例えば入試にこれが出てきて問題を解こうとするとき、解答者がn/mに互いに素という条件をつける意図は何なのでしょうか？
＝＞［作者］：連絡ありがとう．整数の比で表された分数は，もし約分できるものなら約分した形で考えることができます．これが「互いに素」という仮定の意味です（約分しない形のまま扱っていたら分母と分子が確定しません．）
たとえば， $\sqrt{2}=\frac{14142}{10000}$ のまま使うと $n=14142,m=10000$ とすることになりますが，こんなことが許されるなら $n=28284,m=20000;\hspace{10}n=42426,m=30000,\cdots$ もすべてできることなり，ｎ，ｍが定まりません．この分数では $\sqrt{2}=\frac{7071}{5000}$ としてｎ，ｍを確定する必要があります．
本音を言えば，高校生なら誰でも知っているように， $\sqrt{2}=\frac{141421}{100000},\frac{1414213}{1000000},\frac{14142135}{10000000}\cdots$ が有限個の桁で等しくなるとしたら，その約分した結果のn/mについて両辺を２乗したら「分母も分子も2の倍数でなければならないことになるのは矛盾である」という理屈です．
そこで質問を振り返ってみると，n/mが互いに素という仮定を付けないと（既約分数でないものでもそのまま使っているとすると）ｎ，ｍが定まらないことになります．