|
���Z���^�[������� �O�p��
�y�Z���^�[���� 2006�N�x�F���w�h�E�`�i�{�����j ��R��z
�@���̐}�̂悤�Ȓ�����ABCD-EFGH�ɂ����āC AE=, AF=8, AH=10 �Ƃ���D �@���̂Ƃ��CFH=�A�C�ł���Ccos��FAH=�ł���D �܂��C�O�p�`AFH�̖ʐς��I�J�ł���D 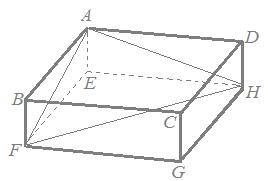
�@���ɁC��AFH�̓����ƕ�AH�̌�_��P�C��FAH�̓����ƕ�FH�̌�_��Q�C����FP�Ɛ���AQ�̌�_��R�Ƃ���D���̂Ƃ��CR�͎O�p�`AFH���N�ł���D����0�`2�̂��������N�ɓ��Ă͂܂���̂���I�ׁD
0�d�S 1�O�S 2���S �@�܂��CAP=�P�ł���C���������āC PF:PR=�R:1 �ƂȂ�D����ɁC�l�ʑ�EAPR�̑̐ς��T�ł���D �m�⑫�����n �@�O�p�`�ɂ����āC
���̊O�ډ~�̒��S���O�S�C
���̓��ډ~�̒��S����S�Ƃ����D �AHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �CHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �EHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �GHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
�IHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �JHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �LHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �NHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �PHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �RHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �THELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �VHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
�y�Z���^�[���� 2007�N�x�F���w�h�E�`�i�{�����j ��R��z
�@��ABC�ɂ����āCAB=2, BC=+1, CA=2�Ƃ���D�܂���ABC�̊O�ډ~�̒��S��O�Ƃ���D (1)�@���̂Ƃ��C��ABC=�A�C���ł���C�O�ډ~O�̔��a�� �ł���D (2)�@�~O�̉~����ɓ_D���C����AC�Ɋւ��ē_B�Ɣ��Α��̌ʂ̏�ɂƂ�D �@��ABD�̖ʐς�S1�C��BCD�̖ʐς�S2�Ƃ���Ƃ� =−1 ……�@ �ł���Ƃ���D��BAD+��BCD=�J�L�N���ł��邩�� CD=AD �ƂȂ�D���̂Ƃ� CD= �ł���D �@����ɁC�Q��AD, BC�̉����̌�_��E�Ƃ��C��ABE�̖ʐς�S3�C��CDE�̖ʐς�S4�Ƃ���D���̂Ƃ� = ……�A �ł���D�@�ƇA��� = ……�A �ƂȂ�D �AHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �CHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �EHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �GHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �IHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �JHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �LHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �NHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
�PHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �RHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �THELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �VHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �XHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �ZHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �\HELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �^HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �`HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �cHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
�y�Z���^�[���� 2008�N�x�F���w�h�E�`�i�{�����j ��R��z
�@��ABC�ɂ����āCAB=7, BC=4, ��ABC=45���Ƃ���D �܂��C��ABC�̊O�ډ~�̒��S��O�Ƃ���D �@���̂Ƃ��CCA=�A�ł���C�O�ډ~O�̔��a�� �ł���D �@�O�ډ~O��̓_A���܂܂Ȃ���BC��ɓ_D��CD=�ł���悤�ɂƂ�D��ADC=�I�J���ł��邩��CAD=x�Ƃ����x�͂Q�������� x2−�Lx−�P�R=0
�����Dx>0�ł��邩��CAD=�T�ƂȂ�D�@�����X�C�Z�C�c�ɂ́C����0�`5�̂������瓖�Ă͂܂���̂�����I�ׁD�������C�������̂��J��Ԃ��I��ł��悢�D 0AC 1AD 2AE 3BA 4CD 5ED �@�_A�ɂ�����O�ډ~O�̐ڐ��ƕ�DC�̉����̌�_��E�Ƃ���D���̂Ƃ��C��CAE=���XE�ł��邩��C��ACE����D�Z�͑����ł���D ������C �@EA=EC �ł���D�܂��CEA2=�c · EC�ł���D���������� �@EA= �ł���C��ACE�̖ʐς��ł���D �AHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �CHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �EHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �GHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �IHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �JHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �LHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �NHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �PHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �RHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
�THELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �VHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �XHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �ZHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �\HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �^HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �`HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �cHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �eHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �gHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �iHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �jHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �kHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �lHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �mHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
�y�Z���^�[���� 2009�N�x�F���w�h�E�`�i�{�����j ��R��z
�@��ABC�ɂ����āCAB=1, BC=, AC=2�Ƃ��C��CAB�̓����ƕ�BC�Ƃ̌�_��D�Ƃ���D �@���̂Ƃ��C��CAB=�A�C�E���ł��� BD= , CD= �ł���D 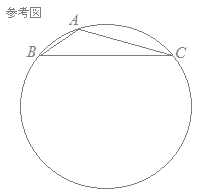 �@AD�̉�������ABC�̊O�ډ~O�Ƃ̌�_�̂���A�ƈقȂ����E�Ƃ���D���̂Ƃ��C��DAB�Ɠ������p�́C����0�`4�̂����P���R�ł���D�������C�P���R�̉̏����͖��Ȃ��D 0��DBE 1��ABD 2��DEC 3��CDE 4��BEC ������CBE=�ł���D�܂��CDE=�ł���D �@���ɁC��BED�̊O�ډ~�̒��S��O’�Ƃ���ƁC O’B= �ł��� tan��EBO’= �ł���D �AHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �CHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �EHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �GHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �IHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
�JHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �LHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �NHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G
�����̖��ł́m�P�n�Ɓm�R�n�̉̏����͖��Ȃ����ƂɂȂ��Ă��܂����C�����ł̓R���s���[�^�ō̓_����s����C�m�P�n<�m�R�n�ƂȂ�悤�ɓ����Ă��������D
�PHELP− ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �RHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �THELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �VHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �XHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �ZHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �\HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �^HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �`HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �cHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
�y�Z���^�[���� 2010�N�x�F���w�h�E�`�i�{�����j ��R��z
�@��ABC��AB=3, BC=4, CA=5�ł��钼�p�O�p�`�Ƃ���D (1) ��ABC�̓��ډ~�̒��S��O�Ƃ��C�~O���R��BC, CA, AB�Ɛڂ���_�����ꂼ��P, Q, R�Ƃ���D���̂Ƃ��COP=OR=�A�ł���D�܂��C QR=�ł���Csin��QPR=�ł���D (2) �~O�Ɛ���AP�Ƃ̌�_�̂���P�ƈقȂ����S�Ƃ���D���̂Ƃ� AP=�ł���CSP=�ł���D �܂��C�_S�����BC���������낵�C������BC�Ƃ̌�_��H�Ƃ���D���̂Ƃ� HP= , SH= �ł���D���������āCtan��BCS=�ł���D (3) �~O��ɓ_T�����RT���~O�̒��a�ƂȂ�悤�ɂƂ�D ���̂Ƃ��Ctan��BCT=�ł���D����āC��RSC=�j�k�� �ł���C��PSC=�l�m���ł���D �AHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �CHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �EHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �GHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �IHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �JHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �LHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �NHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �PHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �RHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
�THELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �VHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �XHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �ZHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �\HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �^HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �`HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �cHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �eHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �gHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �iHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �jHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �kHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �lHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �mHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
�y�Z���^�[���� 2011�N�x�F���w�h�E�`�i�{�����j ��R��z
�@�_O�𒆐S�Ƃ���~O�̉~����ɂS�_A, B, C, D�����̏��ɂ���D�l�p�`ABCD�̕ӂ̒����́C���ꂼ�� AB=, BC=2, CD=, DA=2 �ł���Ƃ���D (1) ��ABC=��, AC=x�Ƃ����ƁC��ABC�ɒ��ڂ��� x2=�A�C−28cos�� �ƂȂ�D�܂��C��ACD�ɒ��ڂ��� x2=15+�E�Gcos�� �ƂȂ�D����āCcos��=, x=�ł���C�~O�̔��a�� �ł���D �@�܂��C�l�p�`ABCD�̖ʐς��R�ł���D (2) �_A�ɂ�����~O�̐ڐ��Ɠ_D�ɂ�����~O�̐ڐ��̌�_��E�Ƃ���ƁC��OAE=�V�X���ł���D�܂��C����OE�ƕ�AD�̌�_��F�Ƃ���ƁC��AFE=�Z�\���ł���C OF · OE=�^ �ł���D �@����ɁC��AD�̉����Ɛ���OC�̉����̌�_��G�Ƃ���D�_E���璼��OG�ɐ��������낵�C����OG�Ƃ̌�_��H�Ƃ���D �@�S�_E, G, �`�͓���~����ɂ���D�`�ɓ��Ă͂܂���̂�����0�`4�����I�ׁD ���������āC OH · OG=�c �ł���D �AHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �CHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �EHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �GHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �IHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
�JHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �LHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �NHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �PHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �RHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �THELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �VHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �XHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �ZHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �\HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �^HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �`HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �cHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
|
�y�Z���^�[���� 2012�N�x�F���w�h�E�`�i�{�����j ��R��z
�@��ABC�ɂ����āCAB=AC=3, BC=2�ł���Ƃ� cos��ABC= , sin��ABC= �ł���C��ABC�̖ʐς��J�C��ABC�̓��ډ~I�̔��a�� �ł���D �@�܂��C�~I�̒��S����_B�܂ł̋������ł���D (1) ��AB��̓_P�ƕ�BC��̓_Q���CBP=BQ ����PQ=�ƂȂ�悤�ɂƂ�D���̂Ƃ��C��PBQ�̊O�� �~O�̒��a���ł���C�~I�Ɖ~O���Z�D�������C�Z �ɂ͎���0�`4���瓖�Ă͂܂���̂���I�ׁD 0�d�Ȃ�i��v����j 1���ڂ��� 2�O�ڂ��� 3�قȂ�Q�_�Ō���� 4���L�_�������Ȃ� (2) �~I��ɓ_E�Ɠ_F���C�R�_C, E, F���꒼����ɂ��̏��ɕ��сC���CCF=�ƂȂ�悤�ɂƂ�D���̂Ƃ� CE= , =�` �ł���D �@����ɁC�~I�ƕ�BC�Ƃ̐ړ_��D�C����BE�Ɛ���DF�Ƃ̌�_��G�C����CG�̉����Ɛ���BF�Ƃ̌�_��M�Ƃ���D ���̂Ƃ��C=�ł���D �AHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �CHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �EHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �GHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �IHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �JHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �LHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |
�NHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �PHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �RHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �THELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �VHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �XHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �ZHELP↓ − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �\HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �^HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �`HELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �cHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G �eHELP − ± 0 1 2 3 4 5 6 7 8 9 A B C D E F G |