【助変数を含むとき】
=\int_{a}^x\mid t-1\mid dt\]) \( \displaystyle f(x)=\int_{a}^x\mid t-1\mid dt \)…(1) \( \displaystyle f(x)=\int_{a}^x\mid t-1\mid dt \)…(1)
の積分記号の中では, xは定数, tが変数
積分記号の外では, xが変数, tは存在しない.
=\int_{a}^b\mid t-x\mid dt\]) \( \displaystyle f(x)=\int_{a}^b\mid t-x\mid dt \)…(2) \( \displaystyle f(x)=\int_{a}^b\mid t-x\mid dt \)…(2)
の積分記号の中では, xは定数, tが変数
積分記号の外では, xが変数, tは存在しない.
tで積分するときは,xは単なる定数として扱い,できあがったxの式をxの関数とします.
【例】
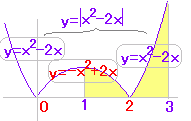
=\int_{0}^x\mid t-1\mid dt\]&chf=bg,s,ffffdd) \( \displaystyle f(x)=\int_{0}^x\mid t-1\mid dt \) \( \displaystyle f(x)=\int_{0}^x\mid t-1\mid dt \)
を xの簡単な式で表してください.
(解答)
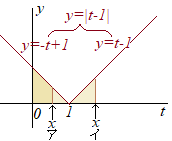 t<1のとき|t−1|=−t+1
t<1のとき|t−1|=−t+1
t≧1のとき|t−1|=t−1
だから
(ア) x<1のとき積分区間0≦t≦xに入るどのtの値に対しても
|t−1|=−t+1
となるから
=\int_{0}^x\mid t-1\mid dt=\int_{0}^x(-t%2B 1)dt\]) \( \displaystyle f(x)=\int_{0}^x\mid t-1\mid dt=\int_{0}^x(-t+1)dt \) \( \displaystyle f(x)=\int_{0}^x\mid t-1\mid dt=\int_{0}^x(-t+1)dt \)
 \( \displaystyle =\left[-\frac{t^2}{2}+ t\right]_0^x=-\frac{x^2}{2}+ x \) \( \displaystyle =\left[-\frac{t^2}{2}+ t\right]_0^x=-\frac{x^2}{2}+ x \)
ここでは0≦xの図で説明したが,実際には積分区間の上端が下端よりも小さくても構わない(上から下を引くだけの計算だから)から,x<0でもよい.
(イ) 1≦xのとき積分区間0≦t≦xは,次の2つの区間に分けられる.
i) 0≦t<1のとき|t−1|=−t+1
ii) 1≦t≦xのとき|t−1|=t−1
=\int_{0}^1(-t%2B 1)dt%2B\int_{1}^x(t-1)dt\]) \( \displaystyle f(x)=\int_{0}^1(-t+ 1)dt+\int_{1}^x(t-1)dt \) \( \displaystyle f(x)=\int_{0}^1(-t+ 1)dt+\int_{1}^x(t-1)dt \)
 \( \displaystyle =\left[-\frac{t^2}{2}+ t\right]_0^1+\left[\frac{t^2}{2}-t\right]_1^x \) \( \displaystyle =\left[-\frac{t^2}{2}+ t\right]_0^1+\left[\frac{t^2}{2}-t\right]_1^x \)
-(\frac{1}{2}-1)) \( \displaystyle =\frac{1}{2}-0+ (\frac{x^2}{2}-x)-(\frac{1}{2}-1) \) \( \displaystyle =\frac{1}{2}-0+ (\frac{x^2}{2}-x)-(\frac{1}{2}-1) \)
 \( \displaystyle =\frac{x^2}{2}-x+ 1 \) \( \displaystyle =\frac{x^2}{2}-x+ 1 \)
|
(2)のように積分変数がtで,それとは異なる文字xとの大小に応じて絶対値記号のはずし方を考えるとき
tで積分するときは,xは単なる定数として扱い,できあがったxの式をxの関数とする事情は(1)と同じですが,xが積分区間の中にある場合には,場合分けして積分することになります.
【例】
=\int_{0}^1\mid t-x\mid dt\]&chf=bg,s,ffffdd) \( \displaystyle f(x)=\int_{0}^1\mid t-x\mid dt \) \( \displaystyle f(x)=\int_{0}^1\mid t-x\mid dt \)
を xの簡単な式で表してください.
(解答)
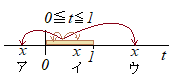 (ア) x<0のとき,積分区間0≦t≦1に含まれるどのtの値もt−x>0を満たすから
(ア) x<0のとき,積分区間0≦t≦1に含まれるどのtの値もt−x>0を満たすから
=\int_{0}^1\mid t-x\mid dt=\int_{0}^1(t-x)dt\]) \( \displaystyle f(x)=\int_{0}^1\mid t-x\mid dt=\int_{0}^1(t-x)dt \) \( \displaystyle f(x)=\int_{0}^1\mid t-x\mid dt=\int_{0}^1(t-x)dt \)
-(0-0)=\frac{1}{2}-x) \( \displaystyle =\left[\frac{t^2}{2}-xt\right]_0^1=(\frac{1}{2}-x)-(0-0)=\frac{1}{2}-x \) \( \displaystyle =\left[\frac{t^2}{2}-xt\right]_0^1=(\frac{1}{2}-x)-(0-0)=\frac{1}{2}-x \)
xは定数だから値が固定されている.
xに先に手を出させてから,tは「後出しジャンケン」をする
(イ) 0≦x<1のとき,積分区間0≦t≦1に含まれるtの値のうち
i) 0≦t<xのとき,t<xだから|t−x|=−t+x
ii) x≦t≦1のとき,t≧xだから|t−x|=t−x
=\int_{0}^1\mid t-x\mid dt=\int_{0}^x(-t%2B x)dt%2B\int_x^1(t-x)dt\]&chs=340x48) \( \displaystyle f(x)\!=\!\int_{0}^1\mid \!t\!-\!x\!\mid\! dt\!=\!\int_{0}^x(\!-\!t+\! x)dt\!+\!\int_x^1(t\!-\!x)dt \) \( \displaystyle f(x)\!=\!\int_{0}^1\mid \!t\!-\!x\!\mid\! dt\!=\!\int_{0}^x(\!-\!t+\! x)dt\!+\!\int_x^1(t\!-\!x)dt \)
 \( \displaystyle =\left[-\frac{t^2}{2}+ xt\right]_0^x+\left[\frac{t^2}{2}-xt\right]_x^1 \) \( \displaystyle =\left[-\frac{t^2}{2}+ xt\right]_0^x+\left[\frac{t^2}{2}-xt\right]_x^1 \)
-(\frac{x^2}{2}-x^2)) \( \displaystyle =-\frac{x^2}{2}+ x^2-0+(\frac{1}{2}-x)-(\frac{x^2}{2}-x^2) \) \( \displaystyle =-\frac{x^2}{2}+ x^2-0+(\frac{1}{2}-x)-(\frac{x^2}{2}-x^2) \)
 \( \displaystyle =x^2-x+\frac{1}{2} \) \( \displaystyle =x^2-x+\frac{1}{2} \)
(ウ) x≧1のとき,積分区間0≦t≦1に含まれるどのtの値もt−x≦0を満たすから
=\int_{0}^1\mid t-x\mid dt=\int_{0}^1(-t%2B x)dt\]) \( \displaystyle f(x)=\int_{0}^1\mid t-x\mid dt=\int_{0}^1(-t+x)dt \) \( \displaystyle f(x)=\int_{0}^1\mid t-x\mid dt=\int_{0}^1(-t+x)dt \)
 \( \displaystyle =\left[-\frac{t^2}{2}+ xt\right]_0^1=-\frac{1}{2}+ x \) \( \displaystyle =\left[-\frac{t^2}{2}+ xt\right]_0^1=-\frac{1}{2}+ x \)
|

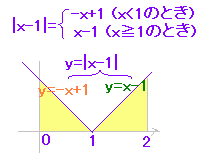


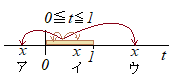 (ア)
(ア)