|
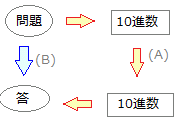
■2進数の演算
○2進数で表された2つの数の和を求めるには
(A)
慣れないうちは
1) 初めに問題を10進数に書き換え 2) 次に10進数で計算して 3) 最後に答を2進数に戻す という方法が考えられます. (B)
慣れてきたら
2進数の演算表を作って,直接計算する こともできます.
【例1】
(解き方A)次の計算をして,結果を2進数で表してください. 1100(2)+1010(2) 1) 初めに問題を10進数に書き換えると 1100(2)=8+4+0+0=12 1010(2)=8+0+2+0=10 2) 次に10進数で計算すると 12+10=22 3) 最後に答を2進数に戻すと 22=1×24+0×23+1×22+1×21+0だから 10110(2) (解き方B)
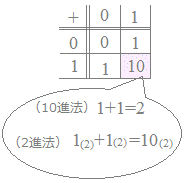
あらかじめ右図2の演算表を作っておきます.
以下(2)は省略重要な箇所はピンクの背景色で示した1箇所だけです. 2進法では数字の0と1しか使わないので,1(2)+1(2)は1つ位が上がって10(2)になります. 1100
+)1010
この問題では,下3桁の計算は繰り上がりがありませんが,最高位の計算で繰り上がりがあります.
|
図1
  |
||
|
(A) 10進数に直して計算する場合
1011(2)=8+0+2+1=11
(B) 2進数で直接計算する場合1101(2)=8+4+0+1=13 13+11=24 24=16+8+0+0+0=11000(2)  →4
|
(A) 10進数に直して計算する場合
10101(2)=16+0+4+0+1=21
(B) 2進数で直接計算する場合(かっこ内は繰り上がってきた数)11111(2)=16+8+4+2+1=31 21+31=52 52=32+16+0+4+0+0=110100(2)
1の位の計算:1+1=10→0を書いて1繰り上げる
以上により,110100(2)2の位の計算:(1)+0+1=10→0を書いて1繰り上げる 4の位の計算:(1)+1+1=11→1を書いて1繰り上げる 8の位の計算:(1)+0+1=10→0を書いて1繰り上げる 16の位の計算:(1)+1+1→1を書いて1繰り上げる 32の位の計算:(1)→1を書く →3
|
|
○2進数で表された2つの数の差,積,商を求めるには
(A)
慣れないうちは
1) 初めに問題を10進数に書き換え 2) 次に10進数で計算して 3) 最後に答を2進数に戻す という方法が考えられます. (B)
慣れてきたら
2進数の演算表を作って,直接計算する こともできます.
【例2】
(解き方A)次の計算をして,結果を2進数で表してください. 1101(2) ×) 1011(2) 1) 初めに問題を10進数に書き換えると 1101(2)=8+4+0+1=13 1011(2)=8+0+2+1=11 2) 次に10進数で計算すると 13×11=143 3) 最後に答を2進数に戻すと 143=1×128+0×64+0×32+0×16+1×8+1×4+1×2+1 だから 10001111(2) (解き方B)
2進数の掛け算は簡単で0を掛けたら何もなしになり,1を掛けたらそのまま同じものになります.(位どりには注意します)
以下(2)は省略1101 ×)1011
11011101 1101 10001111 |

(A) 10進数に直して計算する場合
1001(2)=8+0+0+1=9
(B) 2進数で直接計算する場合11(2)=2+1=3 9×3=27 27=16+8+0+2+1=11011(2) 以下(2)は省略 1011 ×)11
10011001 11011 以上により,11011(2) →2
|
|
【問題4】
次の計算をして,結果を2進数で表してください. 11011(2)×101(2) 110000111(2) 210001011(2) 310010011(2) 410100011(2) 解説
(A) 10進数に直して計算する場合
11011(2)=16+8+0+2+1=27
(B) 2進数で直接計算する場合101(2)=4+0+1=5 27×5=135 135=128+0+0+0+0+4+2+1=10000111(2) 以下(2)は省略 11011 ×)101
1101111011 10000111 以上により,10000111(2) →1
|
(A) 10進数に直して計算する場合
111(2)=7+2+1=7
(B) 2進数で直接計算する場合11(2)=2+1=3 7×3=21 21=16+0+4+0+1=10101(2) 以下(2)は省略 111 ×)11
111111 10101 以上により,10101(2) →2
|
|
【例3】
(解き方B)次の計算をして,結果を2進数で表してください. 101(2) −) 11(2)
以下の問題についても,10進数に直して計算することもできますが,解説はn進数で直接計算する方法だけ書いておきます.
 以下(2)は省略
以下(2)は省略101 −)11
10 |
【例4】
(解き方B)次の計算をして,結果を2進数で表してください. 1100(2) −) 101(2)  1の位を計算するときに,引かれる方が0で引く方が1なので,上の位から借りてきたいのですが,上の位にもないときはさらに上の位から借りてきます.
1の位を計算するときに,引かれる方が0で引く方が1なので,上の位から借りてきたいのですが,上の位にもないときはさらに上の位から借りてきます.まず 100 をくずして 0100 にして,さらに 0110 にします. これで,1の位が引けて1になる. 2の位はそのまま下ろしてくればよい.(1) 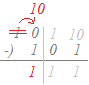 4の位の引き算をするときも,引かれる方が0で引く方が1なので,上の位から借りてくればよい.(今度は1つ上の位の1を借りたらよい).
4の位の引き算をするときも,引かれる方が0で引く方が1なので,上の位から借りてくればよい.(今度は1つ上の位の1を借りたらよい).結果 ⇒ 111(2) |
|
(B) 2進数で直接計算する場合
1の位が足りないので,上の位から借りてくる 1010 −)11
次に2の位も引く方が大きいので,上の位から借りてくる. 01010 −)11
11→2
|
(B) 2進数で直接計算する場合
1の位が足りないので,3つ上の位から順繰りに借りてくる 11000 101000 101100 101110 これで引き算ができます 101110 −)111
10001→2
|
|
【例5】
(解き方B)次の計算をして,結果を2進数で表してください. 101(2) )100011(2)
○ 割り算で,数字を立てるのはむしろ簡単で,入れば1,入らなければ0です.
○ 掛けるときは,割る数の全部に書けます. ○ 割り算の中では,引き算を行います. 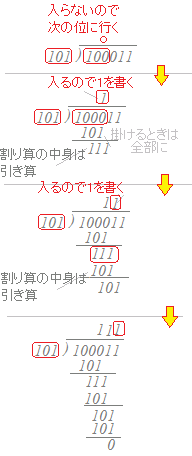 |
(B) 2進数で直接計算する場合(以下,添え字の(2)は略)
10には11は入らないから,その次の位に行く. 101には11が入るから1を立てる. 101−11=10 100←0を下ろしてくる 100には11が入るから1を立てる. 100−11=1 11←1を下ろしてくる 11には11が入るから1を立てる. 11−11=0 結果 ⇒ 111(2) →4
(参考)
Excelで2進数で直接計算する方法は思いつきませんが,10進数経由ならば,次の方法で検算できます. =BIN2DEC(110111)/BIN2DEC(101) によって10進数の結果11が得られるので,これを2進数に直して DEC2BIN(BIN2DEC(110111)/BIN2DEC(101))=1011 となります. 結果 ⇒ 1011(2) →2
|
