【解説】十進法と二進法
十進法とは,0〜9を使って数字を表わし,10になったら位を上げる(10が10個でさらに位を上げる..)書き方です.
二進法とは,0〜1を使って数字を表わし,2になったら位を上げる(2が2個でさらに位を上げる..)書き方です.
例
|
十進法
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
二進法
|
0
|
1
|
10
|
11
|
100
|
101
|
110
|
111
|
1000
|
|
十進法
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
|
二進法
|
1001
|
1010
|
1011
|
1100
|
1101
|
1110
|
1111
|
10000
|
10001
|
十進法による表現と区別するために,十進法以外の表現については,小さなかっこを付けて表わします.
例
10(2)=2 ,100(2)=4, 111(2)=7, 1111(2)=15
各位の数が表わすもの
十進法で表わした123は 1×102+2×10+3
(=100+20+3) です.
2405は 2×103+4×102+0×10+5
(=2000+400+5) です.
(十進法では各位の数が1,10,100,1000,..を何倍するかを表わしています.)
二進法で表わした11(2)は 1×2+1 (=2+1
= 3)です.
101(2)は 1×22+0×2+1
(=4+1
= 5) です.
1111(2)は 1×23+1×22+1×2+1
(=8+4+2+1
= 15) です.
(二進法では各位の数が1,2,4,8,16,32,..を何倍するかを表わしています.
実際には0(ない)と1(ある)だけです.)
【解説】
十進法で表された数を二進法で表すには,次の関係を用いると便利です.
まず
10111(2)=1×24+0×23+1×22+1×2+1
=16+4+2+1
= 23
を例にとって考えます.
23=1×24+0×23+1×22+1×2+1
=2(1×23+0×22+1×2+1)+1
=2(2(1×22+0×2+1)+1)+1
=2(2(2(1×2+0)+1)+1)+1
=2(2(2(2(1)+0)+1)+1)+1
のように変形すると,
1.右端の位の数は23を2で割ったときの余りです
2(2(2(2(1)+0)+1)+1)+1 ・・・・・→ 1
2.このときの商 2(2(2(1)+0)+1)+1
・・・→ 1
をさらに2で割った余りは右から2つ目の位の数です.
3.このときの商 2(2(1)+0)+1
・・・・・・→ 1
をさらに2で割った余りは右から3つ目の位の数です.
4.このときの商 2(1)+0
・・・・・・・・・→ 0
をさらに2で割った余りは右から4つ目の位の数です.
5.このときの商 1
・・・・・・・・・→ 1
をさらに2で割った余りは右から5つ目の位の数です.
右から順
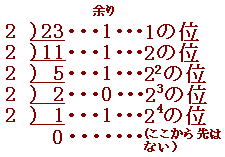 
【 要 点 】
2で割った余りを「右から順」に並べる
|
※ 覚え方としては、「下から順に、左から書く」という解説が多く見られますが、「上から順に右から」というのと同じことになります。
|
