資料の整理／二進法

← PC用は別頁 → 印刷用PDF版は別頁

== 二進法 ==
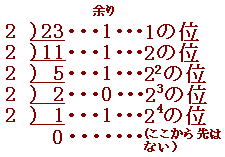
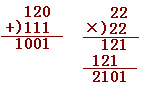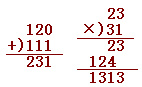■十進法と二進法
○十進法とは，０～９を使って数字を表わし，10になったら位を上げる（10が10個でさらに位を上げる..）書き方です．

○二進法とは，０～１を使って数字を表わし，２になったら位を上げる（２が２個でさらに位を上げる..）書き方です．
【例】

十進法	０	１	２	３	４	５	６	７	８
二進法	0	1	10	11	100	101	110	111	1000

十進法	9	10	11	12	13	14	15	16
二進法	1001	1010	1011	1100	1101	1110	1111	10000

○十進法による表現と区別するために，十進法以外の表現については，小さなかっこを付けて表わします．
【例】

10₍₂₎＝2　，100₍₂₎＝4，　111₍₂₎＝7，　1111₍₂₎＝15

■各位の数が表わすもの
○十進法で表わした数字

123　は　1×10²＋2×10＋3 (=100+20+3)です．
2405　は　2×10³＋4×10²＋0×10＋5(=2000+400+5)　です．

　　（十進法では各位の数が1,10,100,1000,..を何倍するかを表わしています．）

○二進法で表わした数字

11₍₂₎　は　1×2＋1　(=2+1= 3)です．
101₍₂₎　は　1×2²＋0×2＋1 (=4+1= 5)　です．
1111₍₂₎は　1×2³＋1×2²＋1×2＋1(=8+4+2+1= 15)です．

（二進法では各位の数が1,2,4,8,16,32,..を何倍するかを表わしています．
実際には０（ない）と１（ある）だけです．）

*** 二進法はなぜ重要か？ ***
　20世紀の後半以後，コンピュータの発展は社会生活の様々な分野に影響を及ぼすようになってきました．コンピュータでは，電気が流れる（１），電気が流れない（０）の２つを組合せて様々な処理を行っています．この０と１だけからなる信号は二進法に対応しています．
　例えば，次のような「絵」も，■を１，□を０として，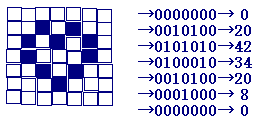

0,20,42,34,20,8,0　で送れます（君にハートを送りますのつもり．）．
　このように，コンピュータが社会生活に深く浸透する中で，計算だけでなく，絵，写真，さらに話し言葉の送受信にも二進法が使われるようになっています．二進法を理解することによってデジタル情報の基本が理解できます．

*** 三進法や五進法はないのか？ ***
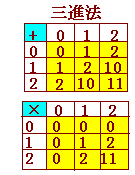
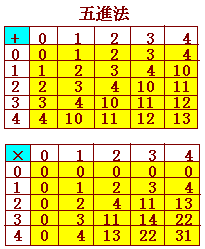
⇒ あります．

　三進法では0,1,2の３つの数を用いて数字を表わし，３になったら１つ位が上がります．（３が３つになればさらに位が上がります．）
例　11₍₃₎＝１×３＋１＝４
　　121₍₃₎＝１×３²＋２×３＋１＝１６

五進法では0,1,2,3,4の５つの数を用いて数字を表わし，５になったら１つ位が上がります．（５が５つになればさらに位が上がります．）
例　401₍₅₎＝４×５²＋０×５＋１＝１０１

次の表は，三進法や五進法での足し算，掛け算の例です．　　

** 十二進法や十六進法ではどんな数字を使うのか？ **

　十二進法では12個の文字，十六進法では16個の文字が必要です．
　特に，１つの文字で10，11などを表わすものがいります．
　このため，0から9までを0,1,2,3,4,5,6,7,8,9で表わし,10以上は通常a,b,c,d,...
　で表わします．（0～9の10文字とa～zの26文字を使えば三十六進法まで表わせます．）

　　例
　　　1b₍₁₂₎＝１×12＋11＝23
　　　ff₍₁₆₎＝15×16＋15＝255

【解説】
　十進法で表された数を二進法で表すには，次の関係を用いると便利です．
　まず
　10111₍₂₎＝1×2⁴＋0×2³＋1×2²＋1×2＋1 =16+4+2+1 = 23
　を例にとって考えます．

23＝1×2⁴＋0×2³＋1×2²＋1×2＋1
　＝2(1×2³＋0×2²＋1×2＋1)＋1
　＝2(2(1×2²＋0×2＋1)＋1)＋1
　＝2(2(2(1×2＋0)＋1)＋1)＋1
　＝2(2(2(2(1)＋0)＋1)＋1)＋1
のように変形すると，
　１．右端の位の数は23を２で割ったときの余りです
　　2(2(2(2(1)＋0)＋1)＋1)＋1　　　・・・・・→　１
　２．このときの商　2(2(2(1)＋0)＋1)＋1 ・・・→　１
　　をさらに２で割った余りは右から２つ目の位の数です．
　３．このときの商　2(2(1)＋0)＋1 ・・・・・・→　１
　　をさらに２で割った余りは右から３つ目の位の数です．
　４．このときの商　2(1)＋0 ・・・・・・・・・→　0
　　をさらに２で割った余りは右から４つ目の位の数です．
　５．このときの商　1 　　　・・・・・・・・・→　1
　　をさらに２で割った余りは右から５つ目の位の数です．

　　右から順

【　要　点　】
２で割った余りを「右から順」に並べる

※　覚え方としては、「下から順に、左から書く」という解説が多く見られますが、「上から順に右から」というのと同じことになります。

【問題】
　十進法で表された次の各数を２進法で表しなさい．

（１）　7=₍₂₎

4,2,1,..と取れるたら取っていくときは
7=4+2+1=1×2²+1×2¹+1=111(2)

縦書きで考えるときは
2 ) 7…1（右端の位）
2 ) 3…1（中間の位）
2 ) 1…1（左端の位）
0

（２）　　11=₍₂₎

8,4,2,1,..と取れたら取っていくときは
11=8+0+2+1=1×2³+0×2²+1×2¹+1=1011(2)

縦書きで考えるときは
2 ) 11…1（右端の位）
2 ) 5…1（右から2つ目の位）
2 ) 2…0（右から3つ目の位）
2 ) 1…1（左端の位）
0

（３）　52=₍₂₎

32,16,8,4,2,1,..と取れたら取っていくときは
52=32+16+0+4+0+0
=1×2⁵+1×2⁴+0×2³+1×2²+0×2¹+0
=110100(2)

縦書きで考えるときは
2 ) 52…0（右端の位）
2 ) 26…0（右から2つ目の位）
2 ) 13…1（右から3つ目の位）
2 ) 6…0（右から4つ目の位）
2 ) 3…1（右から5つ目の位）
2 ) 1…1（左端の位）
0

（４）　　61=₍₂₎

32,16,8,4,2,1,..と取れたら取っていくときは
61=32+16+8+4+0+1
=1×2⁵+1×2⁴+1×2³+1×2²+0×2¹+1
=111101(2)

縦書きで考えるときは
2 ) 61…1（右端の位）
2 ) 30…0（右から2つ目の位）
2 ) 15…1（右から3つ目の位）
2 ) 7…1（右から4つ目の位）
2 ) 3…1（右から5つ目の位）
2 ) 1…1（左端の位）
0

（５）　　98=₍₂₎

64,32,16,8,4,2,1,..と取れたら取っていくときは
98=64+32+0+0+0+2+0
=1×2⁶+1×2⁵+0×2⁴+0×2³+0×2²+1×2¹+0
=1100010(2)

縦書きで考えるときは
2 ) 98…0（右端の位）
2 ) 49…1（右から2つ目の位）
2 ) 24…0（右から3つ目の位）
2 ) 12…0（右から4つ目の位）
2 ) 6…0（右から5つ目の位）
2 ) 3…1（右から6つ目の位）
2 ) 1…1（左端の位）
0

...（携帯版）メニューに戻る

...（PC版）メニューに戻る

■このサイト内のGoogle検索■

△このページの先頭に戻る△【アンケート送信】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．

○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）

質問に対する回答の中学版はこの頁，高校版はこの頁にあります