総和記号,Σ,シグマ

→ 携帯版は別頁 ■総和記号　Σ（シグマ）に慣れよう ○　和を表わす記号Σでは，次のように「式」の形のところの「変数で指定されたものを」「初めの値」から「終りの値まで」「1ずつ増やして」できる項の「和」を表わす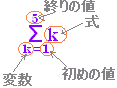．	例1 k = 1+2+3+4+5　（ = 15 になる）例2 k = 1+2+3+4+5+6+7　（ = 28 になる）例3 k = 2+3+4　（ = 9 になる）
○　Σ記号の内部で使う「変数」は，「式」の部分と同じ文字であればよく，どんな文字が使われているかは，和を求めた結果に影響しない．（変数が，式の部分と異なる文字のときは，無関係になりむしろ簡単になる[後出:例6,7参照]）	例4 k = 1+2+3+4　（ = 10 になる） m = 1+2+3+4　（ = 10 になる）
○　「変数」で指定された文字だけを順に増加させるものとし，それ以外の文字や定数は変化させない．	例5 5i = 5･1+5･2+5･3+5･4　(= 5+10+15+20 = 50 になる） (この i は虚数とは関係ない) 例6 n = n+n+n+n　( = 4n になる) 例7 5 = 5+5+5+5　( = 20 になる)
○　「変数」は添字や指数などに使われることもある．	例8 ak = a1+a2+a3+a4+a5 例9 2k = 21+22+23+24 = 2+4+8+16 ( = 30 になる)
○　Σ記号は積でつながっている範囲まで作用する．作用する範囲を明確にするために「かっこ」が使える．	例10 N+1 = ( 1+2+3+4+5 )+1　（ = 16 になる）例11 ( N+1 ) = ( 2+3+4+5+6)　（ = 20 になる）例12 k(k+1)=1･2+2･3+3･4+4･5+5･6=(2+6+12+20+30=70になる) 例13 ( k+1 )2 = ( 1+1 )2+( 2+1 )2+…+( n+1 )2
○　Σ記号が有限個の和を表わすとき，次の性質を満たす．（和差，定数倍のΣは，Σの和差，定数倍になる） (1)　 ( ak+ bk ) = ak+ bk (2)　 cak = c ak （ただし，積や商のΣはΣの積や商とは一般に等しくない．） akbk ≠ ak bk ≠	証明 (1)　 ( ak+ bk ) = ( a1+ b1 )+( a2+ b2 )+…+( an+ bn ) =( a1+a2+…+an )+ ( b1+b2+…+bn ) = ak+ bk (2)　 cak= ca1+ca2+…+can =c( a1+a2+…+an )=c ak
○　括弧を展開して別々に総和を求めることができる．	例14 ( xk - c )2=( xk2 - 2cxk+c2 ) = xk2 - 2cxk+c2

　左欄のΣ記号に等しいものを右欄から選んでください．

はじめに左欄の問題を選択して，続けて右欄の解答を選択してください．やり直すときは，問題を選び直すことからはじめてください．

【問題１】

(k+1)

(k−1)

1+2+3=6

1+2+3+4=10

2+3+4+5=14

2+4+6+8=20

4+4+4+4=16

【問題２】

(2k−1)

(2n+1)

0+2+4+6+8=20

1+3+5+7=16

3+5+7+9=24

k+2k+3k+4k=10k

n+2n+3n+4n=10n

【問題３】

m(m+1)

(j+1)2

2+4+6+8=20

【問題４】

akbk

ak+1

a2+a3+a4+…+an+1

a1+a2+a3+…+an

(a1+a2+a3+…an )(b1+b2+b3+…+bn )

a1b1+a2b2+a3b3+…+anbn

ab+a2b2+…an−1bn−1

++…

【問題５】　次の和をΣ記号を使って表してください．
（正しいものをクリック）

(1)
$2+ 4+ 6+\hspace{3}\cdots\hspace{3}+ 20$

解説やり直す

$\sum_{k=2}^{20} k$ $\sum_{k=1}^{10} k$ $\sum_{k=1}^{10} 2k$ $\sum_{k=2}^{20} 2k$

2, 4, 6, ...の並びを見て，一般項を2kとおく
次に，初項を2にするためにはk=1とする
末項を20にするためにはk=10とする
（k=1からk=10までで全部で10項）
$\sum_{k=1}^{10} 2k$ …（答）

→閉じる←

(2)
$3+ 5+ 7+\hspace{3}\cdots\hspace{3}+ 11$

解説やり直す

$\sum_{k=1}^{11}k$ $\sum_{k=3}^{11} k$ $\sum_{k=1}^{5}(2k-1)$ $\sum_{k=1}^{5}(2k+ 1)$

3, 5, 7, ...の並びを見て，一般項を2k+1とおく
次に，初項を3にするためには2k+1=3よりk=1とする
末項を11にするためには2k+1=11よりk=5とする
（k=1からk=5までで全部で5項）
$\sum_{k=1}^{5}(2k+ 1)$ …（答）
※一般項を2k−1とおくときは
初項を3にするためには2k−1=3よりk=2とする
末項を11にするためには2k−1=11よりk=6とする
（k=2からk=6までで全部で5項）
$\sum_{k=2}^{6}(2k-1)$
ただし，これは選択肢にはないので選べない．

→閉じる←

(3)
$1^2+ 4^2+ 7^2+\hspace{3}\cdots\hspace{3}+ 19^2$

解説やり直す

$\sum_{k=1}^{19}k^2$ $\sum_{k=1}^{6} k^2$ $\sum_{k=1}^{6}(3k+ 1)^2$ $\sum_{k=0}^{6}(3k+ 1)^2$

12, 42, 72, ...の並びを見て，一般項を(3k+1)2とおく
次に，初項を12にするためには3k+1=1よりk=0とする
末項を192にするためには3k+1=19よりk=6とする

k=0も必要に応じて使ってよい

$\sum_{k=0}^{6}(3k+ 1)^2$ …（答）
※一般項を3k−2とおくときは
$\sum_{k=1}^{7}(3k-2)^2$
ただし，これは選択肢にはないので選べない．

→閉じる←

(4)
$1\times 2+ 2\times 3+ 3\times 4+\hspace{3}\cdots\hspace{3}+ 8\times 9$

解説やり直す

$\sum_{k=1}^{8}(k+ 1)$ $\sum_{k=1}^{9} k$

$\sum_{k=1}^{8}k(k+ 1)$ $\sum_{k=1}^{9}k(k+ 1)$

1×2,2×3 ...の並びを見て，一般項をk(k+1)とおく
次に，初項を1×2にするためにはk=1とする
末項を8×9にするためにはk=8とする
$\sum_{k=1}^{8}k(k+ 1)$ …（答）

→閉じる←

【問題６】　Σ記号で表された次の式と等しいものを下の選択肢から選んでください．
（選択肢をクリック）

(1)
$\sum_{k=1}^{n} 2^{k+ 1}$

解説やり直す

$\sum_{k=2}^{n} 2^{k}$ $\sum_{k=2}^{n+ 1} 2^{k}$

$\sum_{k=2}^{n} 2^{k-1}$ $\sum_{k=2}^{n+ 1} 2^{k-1}$

項を並べて書くと，元の式は
$2^2+ 2^3+\hspace{3}\cdots\hspace{3}2^{n+ 1}$
選択肢は順に
$2^2+ 2^3+\hspace{3}\cdots\hspace{3}2^{n}\leftarrow\times$
$2^2+ 2^3+\hspace{3}\cdots\hspace{3}2^{n+ 1}\leftarrow\circ$ …（答）
$2^1+ 2^2+\hspace{3}\cdots\hspace{3}2^{n-1}\leftarrow\times$
$2^1+ 2^2+\hspace{3}\cdots\hspace{3}2^{n}\leftarrow\times$

→閉じる←

(2)
$\sum_{k=1}^{n-1} 3^{2k+ 1}$

解説やり直す

$\sum_{k=3}^{n} 3^{2k-1}$ $\sum_{k=2}^{n} 3^{2k-1}$

$\sum_{k=1}^{2n-1} 3^{k}$ $\sum_{k=3}^{2n-1} 3^{k}$

項を並べて書くと，元の式は
$3^3+ 3^5+\hspace{3}\cdots\hspace{3}+3^{2n-1}$
選択肢は順に
$3^5+ 3^7+\hspace{3}\cdots\hspace{3}+3^{2n-1}\leftarrow\times$
$3^3+ 3^5+\hspace{3}\cdots\hspace{3}+3^{2n-1}\leftarrow\circ$ …（答）
$3^1+ 3^2+\hspace{3}\cdots\hspace{3}+3^{2n-1}\leftarrow\times$
$3^3+ 3^4+\hspace{3}\cdots\hspace{3}+3^{2n-1}\leftarrow\times$

→閉じる←

(3)
$\sum_{k=1}^{n-1} 3\times 2^{k-1}$

解説やり直す

$\sum_{k=0}^{n-2} 3\times 2^{k}$ $\sum_{k=0}^{n-2} 3\times 2^{k+ 1}$

$\sum_{k=2}^{n} 6^{k}$ $\sum_{k=0}^{n-2} 6^{k}$

項を並べて書くと，元の式は
$3+ 3\times 2+ 3\times 2^2+\hspace{3}\cdots+\hspace{3}3\times 2^{n-2}$
選択肢は順に
$3+ 3\times 2+ 3\times 2^2+\hspace{3}\cdots\hspace{3}+3\times 2^{n-2}\leftarrow\circ$ …（答）
$3\times 2+ 3\times 2^2+ 3\times 2^3+\hspace{3}\cdots\hspace{3}+3\times 2^{n-1}\leftarrow\times$
$6^2+ 6^3+ 6^4+\hspace{3}\cdots\hspace{3}+ 6^n\leftarrow\times$
$1+ 6+ 6^2+\hspace{3}\cdots\hspace{3}+ 6^{n-2}\leftarrow\times$
※なお，この種の問題で $6^k$ と混同する答案が多く見られますが，全然関係ないので注意

→閉じる←

(4)
$\sum_{k=1}^{n} 3\times 2^{k+ 1}$

解説やり直す

$\sum_{k=2}^{n+ 1} 3\times 2^{k}$ $\sum_{k=2}^{n+ 1} 3\times 2^{k-1}$

$\sum_{k=1}^{n} 6^{k+ 1}$ $\sum_{k=1}^{n+ 1} 6^{k}$

項を並べて書くと，元の式は
$3\times 2^2+ 3\times 2^3+ 3\times 2^4+\hspace{3}\cdots+\hspace{3}3\times 2^{n+ 1}$
選択肢は順に
$3\times 2^2+ 3\times 2^3+ 3\times 2^4+\hspace{3}\cdots+\hspace{3}3\times 2^{n+ 1}\leftarrow\circ$ …（答）
$3\times 2+ 3\times 2^2+ 3\times 2^3+\hspace{3}\cdots\hspace{3}+ 3\times 2^{n}\leftarrow\times$
$6^2+ 6^3+ 6^4+\hspace{3}\cdots\hspace{3}+ 6^{n+ 1}\leftarrow\times$
$6+ 6^2+ 6^3+\hspace{3}\cdots\hspace{3}+ 6^{n+ 1}\leftarrow\times$

→閉じる←

■［個別の頁からの質問に対する回答］[総和記号について／17.4.6］

問題１の終わりの値が全て4なのに、答えが一つだけ三つの数になっていますまたその影響で、問題１の上から1番目の答えと4番目の問題の答えが同じはずなのに違う判定になっています
＝＞［作者］：連絡ありがとう．あなたは初めの値を見ていないようです．頁の先頭にある例3をよく見てください．

$\sum_{k=1}^4 k=1+ 2+ 3+ 4$
であるが
$\sum_{k=2}^4 k=2+ 3+ 4$
です．

次に，一般項の違いですが

$\sum_{k=1}^4 k=1+ 2+ 3+ 4$
であるが
$\sum_{k=1}^4 (k-1)=0+ 1+ 2+ 3$
です．さらに
$\sum_{k=2}^4 (k-1)=1+ 2+ 3$
です．

■［個別の頁からの質問に対する回答］[総和記号Σ（シグマ）に慣れようについて／16.12.5］

＜Σに慣れよう１＞の問３の、＜一番下の問題=Σ（j＋１）の２乗＞ですが、答えの４の２乗は必要ないのでは？もし必要だとすればそれはなぜでしょうか？
＝＞［作者］：連絡ありがとう．

(j+1)2にj=0を代入すると12
(j+1)2にj=1を代入すると22
(j+1)2にj=2を代入すると32
(j+1)2にj=3を代入すると42

要するに，3+1が4になるからです．あなたの理解は，まだ十分ではないかも･･･

■［個別の頁からの質問に対する回答］[総和記号Σについて／16.11.7］

例12のkが3の時の計算が抜けてる気がします間違ってたらゴメンナサイ…
＝＞［作者］：連絡ありがとう．訂正しました．

...メニューに戻る