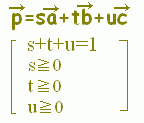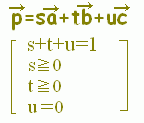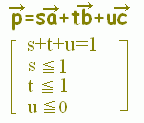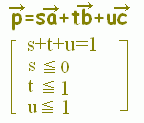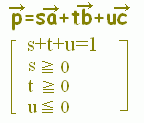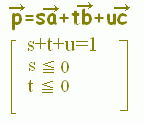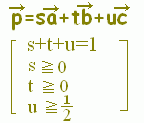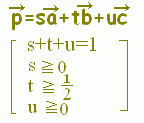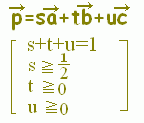|
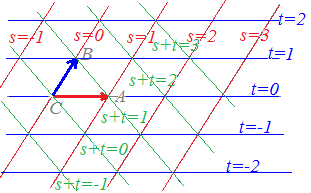
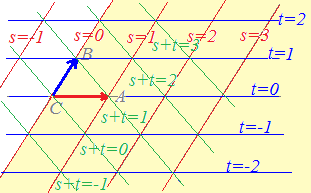
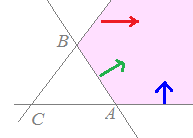
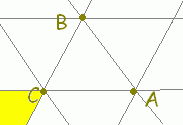
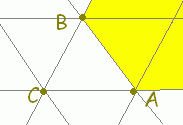
【基本】 平面上の相異なる3点A(),B(),C()が同一直線上にないとき, s+t+u=1・・・(1) は平面全体に対応します。 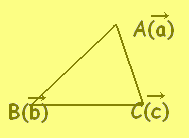
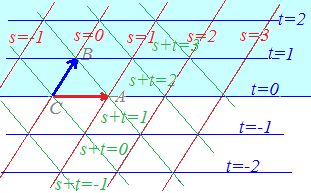
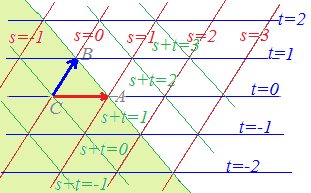
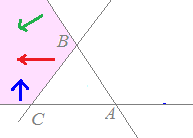
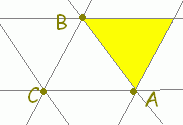
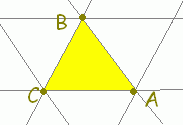
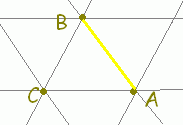
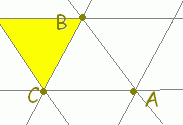
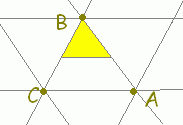
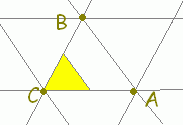
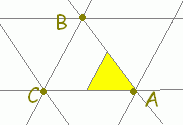
s+t+u=1, s≧0,t≧0,u≧0・・・(2) は△ABCの内部及び周上に対応します。 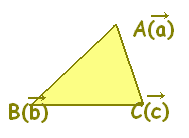
|
|
[解説] (1)← =s+t+u(s+t+u=1)はuを消去して変形すると =s+t+(1−s−t) =+s(−)+t(−) =→OC+s→CA+t→CB まず,→OCにより原点から点Cに進み,次にs→CA+t→CBで平面全体を表すことができます。 (2)← =s+t+u(s+t+u=1, s≧0,t≧0,u≧0) =→OC+s→CA+t→CB( s≧0,t≧0,u=1−s−t≧0) =→OC+s→CA+t→CB( s≧0,t≧0,s+t≦1) は△ABCの内部及び周上となります。 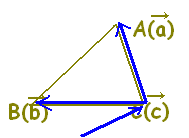 |
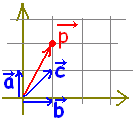 とができるので,3つのベクトルを使うと,同一ベクトルの表し方が何通りも生じます。
とができるので,3つのベクトルを使うと,同一ベクトルの表し方が何通りも生じます。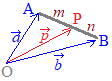 2点
2点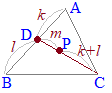 この内分公式を2段階に分けて,次のように組み立てます.
この内分公式を2段階に分けて,次のように組み立てます.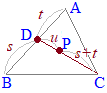 このように,
このように,