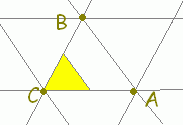
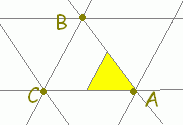
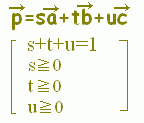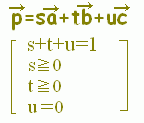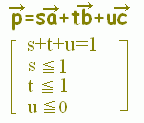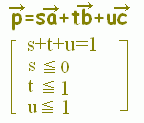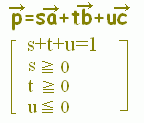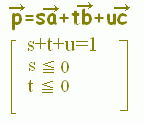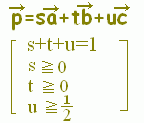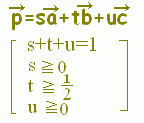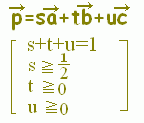【不等式で表される領域を考えるには】
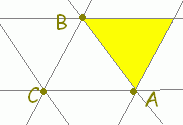
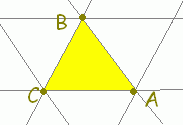
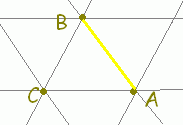
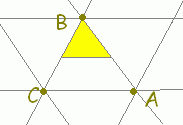
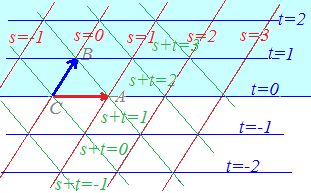
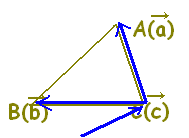
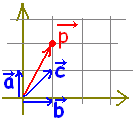
○ \( \displaystyle \vec{p}=s\vec{a}+ t\vec{b}+ u\vec{c} \)(s+t+u=1)すなわち \( \displaystyle \vec{p}=s\vec{a}+ t\vec{b}+ u\vec{c} \)(s+t+u=1)すなわち \( \displaystyle \vec{p}=\vec{c}+ s\overrightarrow{\rm{CA}}+ t\overrightarrow{\rm{CB}} \)で表される点はs, t, s+tの値に応じて次の図形上にあることになります. \( \displaystyle \vec{p}=\vec{c}+ s\overrightarrow{\rm{CA}}+ t\overrightarrow{\rm{CB}} \)で表される点はs, t, s+tの値に応じて次の図形上にあることになります.
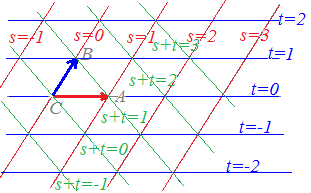
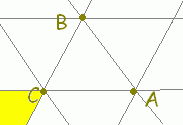
○上の図で,s=−1,0,1,2,...となる場所を順に見て行くと, \( \displaystyle \vec{p}=s\vec{a}+ t\vec{b}+ u\vec{c} \)(s+t+u=1, s≧0)で表される点は次の黄色で示した領域にあることが分かります. \( \displaystyle \vec{p}=s\vec{a}+ t\vec{b}+ u\vec{c} \)(s+t+u=1, s≧0)で表される点は次の黄色で示した領域にあることが分かります.
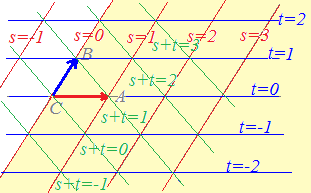
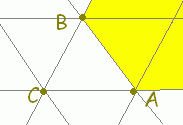
○上の図で,t=−1,0,1,2,...となる場所を順に見て行くと, \( \displaystyle \vec{p}=s\vec{a}+ t\vec{b}+ u\vec{c} \)(s+t+u=1, t≧0)で表される点は次の水色で示した領域にあることが分かります. \( \displaystyle \vec{p}=s\vec{a}+ t\vec{b}+ u\vec{c} \)(s+t+u=1, t≧0)で表される点は次の水色で示した領域にあることが分かります.
|
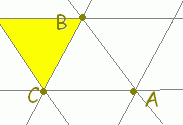
○上の図で,s+t=−1,0,1,2,...となる場所を順に見て行くと, \( \displaystyle \vec{p}=s\vec{a}+ t\vec{b}+ u\vec{c} \)(s+t+u=1, s+t≦1)で表される点は次の緑色で示した領域にあることが分かります. \( \displaystyle \vec{p}=s\vec{a}+ t\vec{b}+ u\vec{c} \)(s+t+u=1, s+t≦1)で表される点は次の緑色で示した領域にあることが分かります.
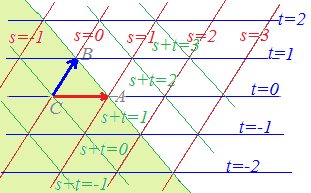

○これらの共通部分を考えることにより,次のような問題が解けます.
【例1】
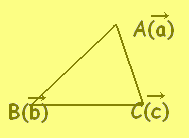
平面上の相異なる3点 \( A(\vec{a}),B(\vec{b}),C(\vec{c}) \)が同一直線上にないとき,
  \( \displaystyle \vec{p}=s\vec{a}+ t\vec{b}+ u\vec{c} \)
s+t+u=1, s≧0, t≧0, s+t≧1 \( \displaystyle \vec{p}=s\vec{a}+ t\vec{b}+ u\vec{c} \)
s+t+u=1, s≧0, t≧0, s+t≧1
で表される領域を答えてください.
次の桃色で示した領域(境界線を含む)
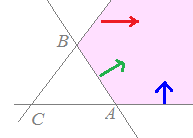
【例2】
平面上の相異なる3点 \( A(\vec{a}),B(\vec{b}),C(\vec{c}) \)が同一直線上にないとき,
  \( \displaystyle \vec{p}=s\vec{a}+ t\vec{b}+ u\vec{c} \)
s+t+u=1, s≦0, t≧0, s+t≦1 \( \displaystyle \vec{p}=s\vec{a}+ t\vec{b}+ u\vec{c} \)
s+t+u=1, s≦0, t≧0, s+t≦1
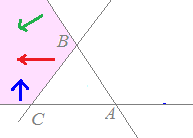
で表される領域を答えてください.
次の桃色で示した領域(境界線を含む)
|
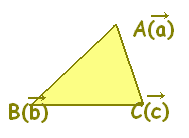
 とができるので,3つのベクトルを使うと,同一ベクトルの表し方が何通りも生じます。
とができるので,3つのベクトルを使うと,同一ベクトルの表し方が何通りも生じます。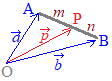 2点
2点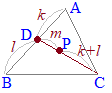 この内分公式を2段階に分けて,次のように組み立てます.
この内分公式を2段階に分けて,次のように組み立てます.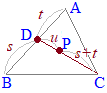 このように,
このように,