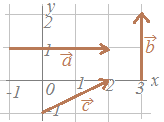|
○小中学校以来学んできたものの量は,単位が決まっていれば,大きさを表す数字を1つで表すことができました.
【例1】 身長 172.5(cm)
【例2】 体重 61.3(kg) 【例3】 面積 80(m2) ○これに対して,「力」「移動」「速度」のような量は,「大きさ」だけでなく「向き」も持った量で表されます.このように「大きさ」と「向き」を持つ量はベクトルと呼ばれ,1つの数字だけでは表せないので矢印を使って表されます. 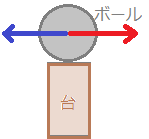 【例1】 力はベクトルで表されます
【例1】 力はベクトルで表されます
台の上のボールがどちらに落ちるかは,力の「大きさ」だけでなく,力の「向き」によって変わる.
 【例2】 移動はベクトルで表されます
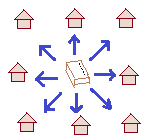
【例2】 移動はベクトルで表されます
荷物が届けられる家は,移動の「大きさ」(=距離)だけでなく,移動の「向き」によって変わる.
【例3】 速度はベクトルで表されます 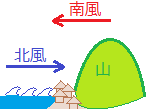
日本海沿岸では,風の速度の「大きさ」(=速さ)だけでなく,風の「向き」によって海の状態が変わる.
南風なら海は静かだが,北風なら海が荒れる. 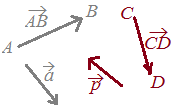 ベクトルの名前の付け方として,始点Aから終点Bに向かうベクトルは,
ベクトルの名前の付け方として,始点Aから終点Bに向かうベクトルは,で表します. などで表します. 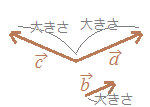 ○「矢印の向き」がベクトルの向きを表しており,「矢印の長さ」がベクトルの大きさを表しています.
○「矢印の向き」がベクトルの向きを表しており,「矢印の長さ」がベクトルの大きさを表しています.右図のベクトルについては, |
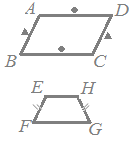
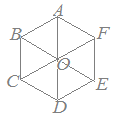
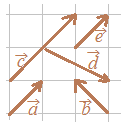
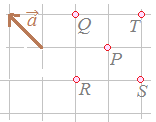
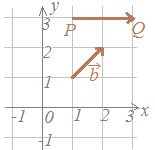 【例】
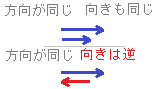
【例】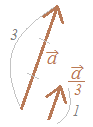 ※ベクトルの「向き」表す記号はないのか?
※ベクトルの「向き」表す記号はないのか?